Метод логарифмических амплитудно-частотных характеристик для синт. Корр. Устр,

1. Строят асимптотическую ЛАЧХ L_H неизменяемой части системы. Эта часть содержит объект регулирования, исполнительное устройство, элемент основной обратной связи, элемент сравнения, а также усилитель. Асимптотическую ЛАЧХ L_H строят по передаточной функции неизменяемой части системы (разомкнутой).

2. Строят желаемую ЛАЧХ L_ж разомкнутой системы. L_ж условно разделяют на три части:

§ низкочастотная часть - определяет точность в установившихся режимах (статическую точность системы). В статической системе низкочастотная асимптота параллельна оси абсцисс. В астатической системе наклон этой асимптоты составляет —20ν дБ/дек, где ν - порядок астатизма (равный 1, 2,...). Ордината L _ж при lgw=0 равна 20lg κ, где κ - передаточный коэффициент разомкнутой системы.

§ среднечастотная часть определяет устойчивость, запас устойчивости а следовательно, качество переходных процессов, и наиболее важна. Основные параметры среднечастотной асимптоты - ее наклон и частота среза w_с, при которой L_ж пересекает ось абсцисс. Чем больше наклон среднечастотной асимптоты, тем труднее обеспечить хорошие динамические свойства системы. Наиболее целесообразен наклон -20 дБ/дек и крайне редко он превышает -40 дБ/дек. w_с определяет быстродействие системы - чем больше w_с, тем выше быстродействие, тем меньше время регулирования t_p переходной характеристики.

§ высокочастотная часть - слабо влияет на динамические свойства системы.

Упрощенное построение желаемой ЛАЧХ:

а. Определить необходимую частоту среза w_с = κ₀ π/ t_р. κ₀ выбирается по графику:

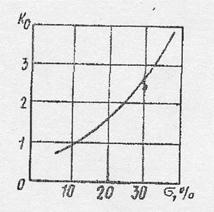
b. Вычислить границы среднечастотной части w_гр1 = w_с /w_гр2, w_гр2 = (2÷4)w_с (например 3) c. В установленных границах провести через точку (lg w_C, 0 дБ) асимптоту под углом -20дБ/дек.

d. Соединить дополнительной асимптотой (угол наклона кратен 20дБ/дек, обычно -40дБ/дек) среднечастотную асимптоту L_ж с L_H в области низких частот. Т.е. на малых частотах L_ж и L_H будут совпадать.

е. В высокочастотной части продолжить среднечастотную асимптоту L_ж

высокочастотной, параллельной асимптоте L_H в области высоких частот. 3.Графически определяют разность L_k = L_Ж - L_H. Для этого при каждой из сопрягающих частот характеристик L_H и L_ж вычисляют разность их ординат, полученные точки наносят на график и соединяют отрезками прямых. Получается график ЛАЧХ необходимого последовательного корректирующего устройства, которое включают непосредственно после элемента сравнения или после предварительного усилителя. По графику определяют передаточную функцию последовательного корректирующего устройства. Можно сделать иначе - по L_ж определить передаточную функцию W _ж и использовать формулу W_Kopp = W _ж / W _Н. По W_Kорр подбирают корректирующее устройство.

Дата добавления: 2014-01-05