Основные понятия и определения. Основные задачи теории телетрафика

Основные задачи теории телетрафика

Основная цель теории телетрафика заключается в разработке методов оценки качества функционирования систем распределения информации. В соответствии с этим на первом месте в теории телетрафика стоят задачи анализа, т. е. отыскание зависимостей и значений величин, характеризующих качество обслуживания, от характеристик и параметров входящего потока вызовов, схемы и дисциплины обслуживания. Эти задачи в начальный период развития телефонной техники были более актуальными, чем задачи синтеза, и решались, как правило, с помощью теории вероятностей.

Поэтому наиболее значительные результаты на сегодняшний день получены при решении задач анализа.

Развитие координатной и особенно квазиэлектронной и электронной коммутационной техники поставило перед теорией телетрафика сложные вероятностно-комбинаторные задачи синтеза, в которых требуется определить структурные параметры коммутационных систем при заданных потоках, дисциплине и качестве обслуживания.

Близкими к задачам анализа и синтеза являются задачи оптимизации. Эти задачи при проектировании систем распределения информации формулируются следующим образом: определить такие значения структурных параметров коммутационной системы (алгоритмы функционирования), для которых: 1) при заданных потоках, качестве и дисциплине обслуживания стоимость или объем оборудования системы распределения информации минимальны и 2) при заданных потоках, дисциплине обслуживания и стоимости качественные показатели функционирования системы распределения информации оптимальны.

При эксплуатации систем распределения информации задача оптимизации формулируется как задача управления потоками вызовов или структурой системы для достижения наилучших показателей качества функционирования. Из-за больших вычислительных трудностей задачи оптимизации систем распределения информации начали ставиться и решаться в последние два десятилетия после появления быстродействующих ЭВМ.

Последовательность сообщений [занятий] создает нагрузку на системы передачи и коммутации. Она определяется потоком вызовов и длительностью занятий.

Вызов - требование источника на установление соединения или передачу сообщения.

Поток вызовов -последовательность моментов поступления вызовов.

Длительность занятия -среднее время, в течение которого занят обслуживающий прибор при одном занятии

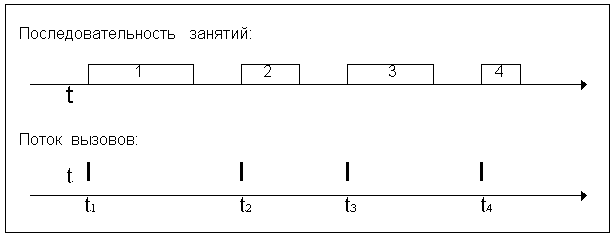
Последовательность занятий:

В общем случае потоки вызовов являются случайными процессами. Точное математическое описание потоков невозможно, поэтому используются их модели. Свойства моделей упрощают описание потоков

Свойства моделей потоков:
- Стационарность - независимость вероятностных характеристик от времени
- Отсутствие последействия - независимость от предыдущего состояния
- Ординарность - появление одновременно только одного вызова

Наиболее распространена модель в виде простейшего потока вызовов.

Простейший поток - стационарный ординарный поток без последействия.

Распределение числа вызовов во времени для простейшего потока характеризуется законом Пуассона, а распределение длительности промежутков между вызовами подчинено экспоненциальному закону

Одной из важнейших числовых характеристик простейшего потока является параметр потока или его интенсивность

Важно, что при объединении простейших потоков получается также простейший поток вызовов с параметром, равным сумме параметров исходных потоков. При разделении потоков - аналогично.

В большинстве случаев поток вызовов в часы наибольшей нагрузки (ЧНН) от группы источников численностью > 100 удовлетворительно описывается простейшим потоком.

В том случае, если число источников меньше 100, используют модель примитивного потока.

Примитивный поток - ординарный поток, параметр которого прямо пропорционален числу свободных источников.

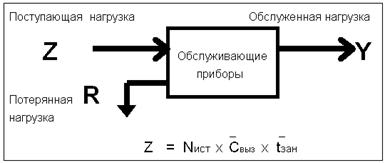Телефонная нагрузка - общая длительность занятия обслуживающих приборов в течение некоторого промежутка времени.

Единица измерения нагрузки 1 часо-занятие

Интенсивность телефонной нагрузки - величина нагрузки в единицу времени. Измеряется в Эрлангах

1 Эрл = 1 часо-эанятие / час

Интенсивность телефонной нагрузки имеет сильные колебания, в том числе и в течение дня.

Час наибольшей нагрузки [ЧНН] - период суток, в течение которого нагрузка имеет наибольшее значение

Коэффициент концентрации нагрузки: Кк = Yчнн / Y сут
К к = 0,1 для Москвы
К к = 0,11 для Санкт- Петербурга
К к = 0,14 для областных центров
К к = 0,19 для районных центров

Распределение нагрузки, поступающей от одного источника на несколько потребителей описывается коэффициентом распределения нагрузки

Потери - часть поступающей нагрузки, которая не обслуживается из-за занятости обслуживающих приборов.

Различают виды коммутационных систем:
- коммутационные системы без потерь
- коммутационные системы с потерями
- коммутационные системы с ожиданием

Потери измеряются в процентах или в промилле [0,1 %] и рассчитываются как отношение потерянной нагрузки R к поступающей Z.

Нормативы:
На ГТС между двумя ТА на одной ГТС р<= 0,03
На ЗТС между двумя ТА разных местных сетей одной зоны <= 0,03 - 0,13
На МТС между двумя ТА разных зон семизначной нумерации <= 0,1

Дата добавления: 2014-01-05