Виды АИМ модуляции

Различают сигналы АИМ 1-го и 2-го рода. АИМ сигнал 1-го рода является результатом дискретизации непрерывного сигнала на интервалах Котельникова. При этом вершина каждого импульса меняется в соответствии с изменением мгновенного значения сигнала.

Такой сигнал не может быть использован для последующего кодирования, т.к. изменения амплитуды импульса в процессе кодирования исказит кодовую комбинацию. Для этого отсчетное значение импульса на интервале кодирования остается неизменным. Такой сигнал называется сигналом АИМ-2 рода.

Для получения этого сигнала достаточно запомнить мгновенное значение импульса в начале отсчета и удерживать его в памяти в течение всего времени t_u.

На рисунке 3.2 представлены сигналы АИМ1 и АИМ 2 рода.

Рисунок 3.2. К пояснению принципов формирования АИМ-I и АИМ-II

Различие между сигналами АИМ-I и АИМ-II оказывается существенным, если длительность импульсов τ сравнима с периодом их следования Т.

Поскольку все реально существующие непрерывные сигналы связи представляют собой случайные процессы с бесконечно широким спектром, причем основная энергия сосредоточена в относительно узкой полосе частот, перед дискретизацией на передаче необходимо с помощью фильтра нижних частот ограничить спектр канала некоторой частотой F_в. Для ТФ сигналов необходимо использовать ФНЧ с частотой среза F_в = 3, 4 кГц.

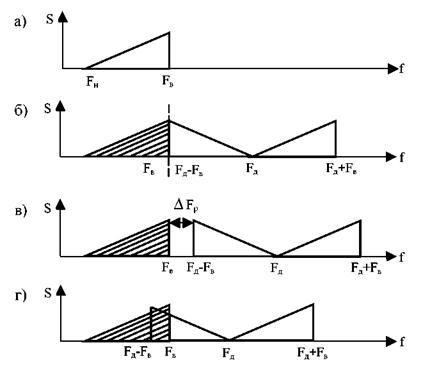
Рисунок 3.3. Влияние частоты дискретизации на возможность восстановления сигнала с помощью фильтра

Рассмотрим требования, предъявляемые к выбору частоты дискретизации, с точки зрения возможности выделения первичного сигнала при приеме за счет использования фильтрации низкочастотной части спектра. На рис.3.3а изображен спектр первичного сигнала, а на рис.3.3б-г - спектры S_В (F) при разных соотношениях между F_д и F_в. Если в соответствии с теоремой Котельникова выбрана F_д = 2F_в, то частоты F и F_д - F_в совпадают и спектр первичного сигнала может быть отделен от нижней боковой АИМ сигнала, лежащей в диапазоне от F_д - F_в до F_д; только с помощью идеального ФНЧ, который физически нереализуем. Поэтому на практике выбирают F_д > 2F_в. В этом случае спектры F_н - F_в и (F_д - F_в) ÷ F_в разнесены и можно выделить первичный сигнал реальным фильтром. Обычно принимают F_д = (2, 3 ÷ 2, 4) F_в. Так при дискретизации ТФ сигнала со спектром 0,3…3,4 кГц F_д = 8 кГц. При этом полоса расфильтровки ∆ F оказывается достаточно большой и составляет ∆ F = (F _д - F_в)- F_в = 1, 2 кГц.

Как видно из рис. 3.2 АИМ сигнал является дискретным по времени, но непрерывным по уровню, т.к. амплитуда отсчетов может принимать бесконечное множество значений. Это потребует при кодировании использования кодов с числом разрядов, стремящихся к бесконечности. Поэтому ограничивают число возможных значений амплитуд АИМ отсчетов конечным множеством, содержащим определенное число «разрешенных» уровней N_кв. Это достигается в процессе квантования сигнала по уровню, при котором истинное значение каждого АИМ отсчета заменяется ближайшим разрешенным значением. Значение N_кв зависит от вида передаваемого сигнала и требований к качеству передачи. Помимо общего числа уровней квантования N_кв квантующее устройство характеризуется шагом квантования δ и напряжением ограничения U_огр. Шагом квантования δ называют разность между двумя соседними разрешенными уровнями, а U определяет максимальное значение амплитуды отсчета, подвергаемого квантованию. Необходимо, чтобы вероятность появления отсчета с амплитудой выше U_огр была пренебрежимо мала. Очевидно δ = U₀ / N. Если шаг квантования во всем диапазоне изменений амплитуды сигнала остается постоянным, т.е. δ = сonst, то квантование называется равномерным. Если в пределах шкалы шаг квантования не остается постоянным, то квантование называется нелинейным (неравномерным).

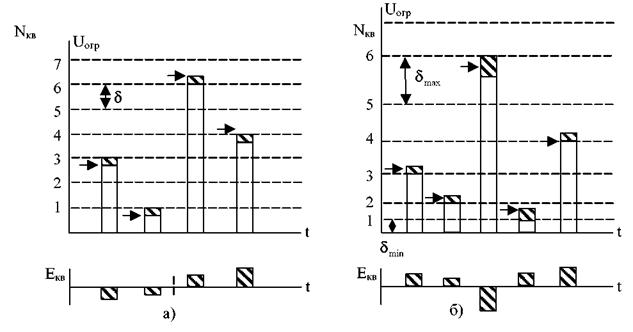Рис.3.4. Принципы равномерного (а) и неравномерного квантования (б)

На рис. 3.4 и 3.5 показаны принципы равномерного и неравномерного квантования и амплитудные характеристики квантующих устройств. Квантование осуществляется следующим образом. Если амплитуда отсчета в пределах двух соседних разрешенных уровней превышает половину шага квантования ∆ / 2, то амплитуда отсчета изменяется в большую сторону, если меньше половины шага квантования - в меньшую сторону. Т.О. операция квантования аналогична операции округления чисел, а следовательно, неизбежно приводит к возникновению ошибки, причем устранить эту ошибку на приеме не представляется возможным. Ошибкой (шумом) квантования называют разность между истинным значением отсчета и его квантованным значением: Z_кв (t) = U_аим (t)- U_кв (t). На рис. 4 истинное значение амплитуды каждого АИМ отсчета (до операции квантования) указано стрелкой. Как видно из рис., вне зависимости от амплитуды отсчета |Z (t)| < ∆ / 2. При этом, средняя мощность шумов квантования при равномерном _кв квантовании Р_ш.кв =∆²/12.

Рисунок 3.5. Амплитудные характеристики квантующих устройств

Характеристика квантования (рис.3.5) имеет две зоны: квантования при |U_вх| < |U_огр| и ограничения при |U_вх| > |U_огр|. Зона квантования является рабочей областью характеристики. В ее пределах осуществляется квантование сигнала. Чтобы не возникали шумы ограничения, применяют специальные меры, предотвращающие перегрузку квантования, т.к. возникающие шумы ограничения имеют мощность значительно превышают мощность шумов квантования.

Основной недостаток равномерного квантования заключается в следующем. Поскольку мощность шумов квантования не зависит от величины сигнала, защищенность от шумов квантования, определяемая как А₃ = 10 lg P / P оказывается небольшой для сигналов с малыми уровнями (слабых сигналов) и возрастает при увеличении уровня сигнала (рис.3.4). Для того чтобы выполнить требование к защищенности А_3кв, необходимо уменьшить шаг квантования, т.е. увеличить число разрешенных уровней. При уменьшении ∆в 2 раза мощность шумов квантования уменьшается в 4 раза, а защищенность А₃ возрастает на 6 дБ.

Число уровней квантования N_кв однозначно связано с разрядностью кода т, необходимой для кодирования квантованных АИМ отсчетов. При использовании двоичных кодов N_кв = 2 ^т.

Для т ах по амплитуде сигнала защищенность от шумов квантования А_{3кв max} = 6m - 9, 2 дБ, а для слабых сигналов А_{3кв min} = 6m - 42, 2 дБ.

Если требуется обеспечить защищенность от шумов квантования во всем динамическом диапазоне сигнала не менее А_{3кв . тр} = 30 дБ, то оказывается, что потребуется

m = 12 (4096N_кв). При этом защищенность для сигналов т ах с амплитудой (сильных) будет более чем на 30 дБ превышать А_{3кв . тр} .

Большое число разрядов в коде (т = 12) при равномерном квантовании приводит к усложнению аппаратуры и неоправданному увеличению тактовой частоты. Устранить указанный существенный недостаток можно, осуществляя неравномерное квантование, которое используется в современных ЦСП. Для слабых сигналов шаг квантования выбирается и постепенно увеличивается, достигая максимальных значений для сильных сигналов (рис. 3.4б).

Дата добавления: 2014-01-05