Счетчик Джонсона

Схема счетчика Джонсона и временная диаграмма его работы приведены на рис. 4.11 б) и в).

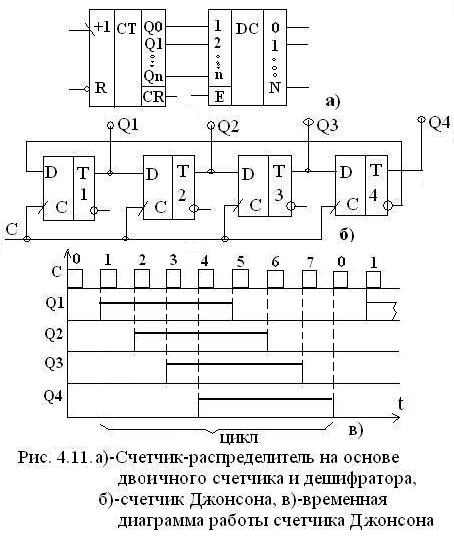
Работа счетчика. Начальное состояние – все разряды в «0». 1-й импульс С установит триггер Т1 в «1» (поскольку 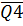=1). В остальных разрядах останется «0» как результат сдвигов «0» от соседних разрядов слева. Второй импульс С сохраняет «1» в Т1 и записывает ее в Т2. В остальных разрядах остается «0». Последующие сдвиги приведут к заполнению единицами всех разрядов, то есть пройдет волна единиц и в счетчике окажется слово 1111. 5-й импульс С установит в Т1 «0» (поскольку теперь 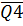=0) и далее пройдет волна «0», в счетчике окажется слово 0000. Далее цикл повторяется: сначала 1111, потом 0000. Особенность схемы: при любом числе n-разрядов. Число состояний счетчика равно 2n – четное. Полученный код представлен уровнями сигналов (см. временную диаграмму рис.4.11 в), поэтому часто его преобразуют (дешифруют).

Принцип дешифровки основан на выявлении характерной временной координаты на временной диаграмме: границы между зонами единиц и нулей.

Рассмотрим таблицу кодов на выходе счетчика (рис.4.12 а). В двух случаях: для слов 0000 и 1111 – состояние счетчика выявляется анализом крайних разрядов 1 и 4. Этого достаточно (см. табл.). В остальных случаях анализируются разряды на границе единиц и нулей.

На основе этого анализа можно составить уравнения выходов дешифратора в счетчике Джонсона, представленные на рис.4.12 б), где Fi (i=0,1,…7) – значения выходов дешифратора, соответствующие состояниям счетчика.

Схема соответствующего дешифратора и временная диаграмма его работы приведены на рис.4.12 в) и г) соответственно. Подсоединив входы полученной схемы дешифратора к выходам счетчика Джонсона на выходах Fi получим распределитель импульсов.

Примечание:

1).Такие счетчики иногда называют счетчиками Мебиуса (открыл ленту 8), Либау-Крейга (ими открыт код счетчика Джонсона).

2).В схеме счетчика всегда четное число состояний. Если необходимо иметь нечетное число, то проблему можно решить одним из ранее рассмотренных способов исключения лишних состояний.

В рассмотренной схеме можно исключить последнее и перейти к следующему, то есть перейти от комбинации 11…11 к комбинации 11…10, которое создает «1» в предпоследнем разряде на прямом выходе и «0» на инверсном, который можно подать на вход счетчика вместе с основным сигналом обратной связи (с 7 разряда на 0 разряд) через конъюнктор.

3). Схема счетчика Джонсона может попасть в одно из неиспользуемых состояний при сбое и будет работать с ним. Для придания свойства самовосстановления можно вырабатывать сигнал обратной связи, который восстановит счетчик в соответствии с соотношением:

Fо.с.=˅.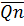

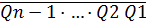4).Рассмотренный счетчик характеризуется небольшими аппаратными затратами:1/2 триггера+1 элемент И на канал распределения, и достаточно высоким быстродействием.

Пример серийно выпускаемых распределителей (счетчиков) К561ИЕ9 (трехразрядный), ИЕ19 (пятиразрядный).

Дата добавления: 2014-01-05