Компараторы

Полиномиальные счетчики.

Это сдвигающие регистры с линейными обратными связями, генераторы псевдослучайных последовательностей. Используются в устройствах тестового диагностирования цифровых устройств, решения задач методом Монте-Карло, моделировании систем с учетом разброса их параметров и в ряде других случаев.

Название «полиномиальные» связано с понятием линейных комбинационных функций. На рис.4.14 б) приведена схема полиномиального счетчика. При нулевых состояниях всех триггеров и при IN=0 счетчик не реагирует на С-сигналы. При подаче IN=1 (причем только одной) по очередному сигналу С счетчик переходит в состояние 100, и далее при IN=0 в каждый такт схема меняет состояние по некоторому закону. Схема входит в цикл и будет работать в нем, пока по входу гашения R все триггеры будут сброшены в «0».

Длина и вид генерируемой последовательности зависят от числа триггеров в счетчике и от того, между какими разрядами заведены О.С. и включены сумматоры по mod2.

В заключение, полиномиальные узлы а базе сдвигающих регистров и сумматоров по mod2 способны реализовать ряд операций над полиномами (многочленами), имеющими двоичные коэффициенты при степенях переменной Х (пример – циклические коды).

Компаратор – это узел для сравнения двух чисел. Простейший компаратор сравнивает 2 числа (слова) А и В и выдает однобитовый сигнал: при равенстве А=В –>1, при неравенстве – 0.

Полный компаратор сравнивает А и В и определяет соотношения: A=B, A>B и A<B.

При построении компаратора преодолевается основная трудность: определение указанных соотношений – функций.

Сравнение двух чисел происходит на основе поразрядных операций над одноименными разрядами обоих чисел.

Признаки равенства разрядов сформулированы и приведены на рис.4.15 а).

На основе полученных выражений для функции F_Ai=Bi построена схема сравнения одноименных разрядов чисел А и В, которая приведена на рис. 4.15 б). Функции F_A>B и F_A<B можно получить на основе следующих рассуждений:

при a2=1 и b2=0 – слово А>B

при a2=0 и b2=1 – слово А>В.

При а2=b2 результат сравнения будет неизвестным, поэтому нужен анализ более младших разрядов. Следовательно, для трехразрядных слов можно записать выражения для F_A>B и F_A<B, которые приведены на рис. 4.16 а).

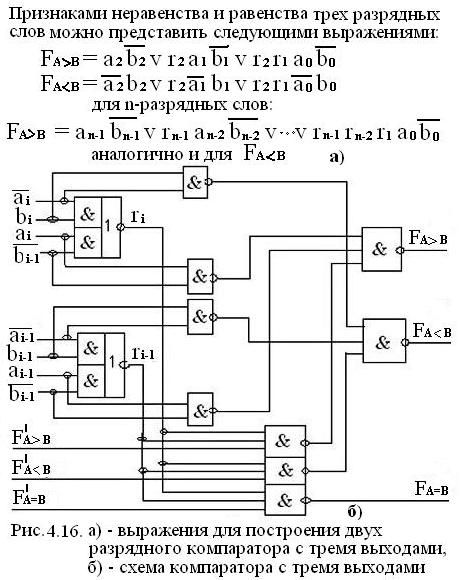
В соответствии с полученными выражениями для F_A=B,F_A>B и F_A<B построен компаратор для сравнения двух двухразрядных чисел А и В, схема которого приведена на рис.4.16 б).

Компаратор можно построить и на основе сумматора, используя операцию вычитания чисел А-В, для чего число В достаточно представить в обратном коде, после чего сложить и прибавить 1 младшего разряда.

По результатам такого суммирования можно выделить признаки, по которым определить соотношения:

А>B –>CR=1 S≠0 на основе этих признаков построена схема

A=B –> CR=1 S=0 компаратора приведения на рис. 4.17 б).

A<B –> CR=0 S≠0

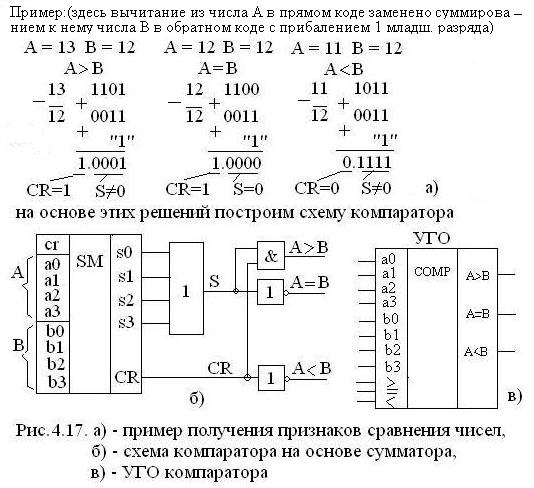
По затратам оборудования такая схема уступает предыдущей (сумматор сложнее). УГО компаратора показано на рис. 4.17 в). Серийно выпускаемые COMP К561ИП2, К555СП1. Входы > = < – для наращивания разрядности.

Глава 5. Сумматоры.

Дата добавления: 2014-01-05