Сумматор

На основании таблицы суммирования двух разрядов чисел А и В (рис.5.2) можно составить логические выражения при суммировании для суммы S и переноса CR (выражения ).

Основная задача – минимизировать эти функции. После минимизации получим функции суммирования для суммы S и переноса CR. На основании функций можно построить одноразрядный сумматор – рис.5.3 а).

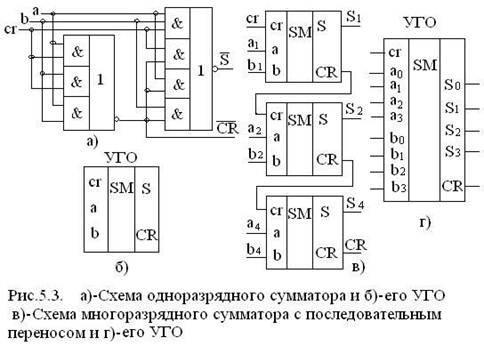
Следует отметить, что схема одноразрядного сумматора, построенная на основании функций 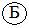в базисе И-ИЛИ-НЕ имеет 17 выводов, что в 2 раза меньше, чем в схеме, построенной на основании функций 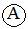(цена минимизации).

Задержка сумматора: для S – 1τ, для CR – 2τ. Последовательным соединением одноразрядных сумматоров по тракту переноса CR получен многоразрядный сумматор с последовательным переносом (рис.5.3 в), его УГО на рис.5.3 г.

Особенности схемы.

На входе одноразрядного сумматора сигнал cr, а на выходе – 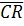, следовательно, между разрядами надо ставить инверторы, что увеличивает задержку многоразрядного сумматора. Поэтому на практике для решения этой проблемы используется свойство самодвойственности логических функций: значение функции интерпретируется при инвертировании ее входных аргументов. Это видно из сравнения строк таблицы суммирования (рис.5.2): 3 и 4, 2 и 5, 1 и 6, 0 и 7. Исходя из этого факта при построении многоразрядного последовательного сумматора тракты переноса CR соединяются напрямую, а на те разряды, на которые поступает инверсный перенос 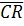, входные аргументы инвертируют и получают на выходе CR без инверсии. Если на входы разрядов сумматора данные подаются с выходов регистра (это чаще всего и делается), то данные для соответствующих разрядов снимаются с инверсных выходов этого регистра.

По определению сумматором называют комбинационное логическое устройство для выполнения арифметического сложения двух чисел, представленных в двоичном коде. Сумматор является основным узлом арифметико-логического устройства ЭВМ – ALU.

Сумматор имеет:

n – входов разрядов числа А.

n – входов разрядов числа В.

cr – вход переноса из младшего разряда сумматора.

CR – выход переноса в старший разряд сумматора.

n – выходов разрядов суммы S.

Задержки распространения сигналов:

t_cr,S – от входа переноса до установления суммы S.

t_А,S– от входов слагаемых до выходов S при cr – const.

t_cr,CR– от входа cr до выхода CR при постоянных слагаемых.

t_A,CR– от входа слагаемых до выхода CR.

Задержка многоразрядного сумматора с последовательным переносом:

t_{cr вх,СR вых}= t_cr1,CR1+ t_cr2,CR2+… +t_{cr n,CR n}=n t_cr,CR,

где n – число разрядов в сумматоре,

t_cr,CR – задержка в одном разряде.

Примеры серийно выпускаемых сумматоров:

К155ИМ1 – двухразрядный, данные вводятся с регистра – прямой и инверсный выход,

К155ИМ-2,3 – четырехразрядные, с переносом через разряд, используется инвертор.

Иногда в сумматорах для решения проблемы переносов в разрядах используются сумматоры с двухколейным переносом (рис. 5.4 а и б).

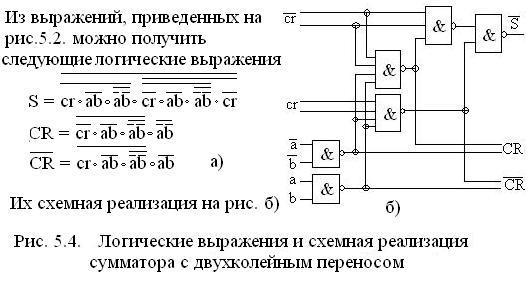
Логические функции суммирования (а) получены из соотношений 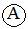(рис. 5.2). Схема реализации рис. 5.4 б.

Особенности схемы: перенос вырабатывается парафазным кодом по двум трактам CR и 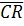, что позволяет при построении многоразрядного сумматора для переноса между разрядами CR или 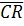для получения суммы всегда одной фазности.

§ 5.3 Сумматоры с параллельным переносом.

Сумматоры с параллельным переносом не имеют последовательного распространения сигнала переноса от разряда к разряду. Во всех разрядах перенос формируется специальными схемами, на входы которых одновременно поступают все переменные, необходимые для его выработки.

Суть построения сумматора с параллельным переносом поясняет его структурная схема, показанная на рис. 5.5.

Основной задачей в таком сумматоре является построение специальной схемы для формирования сигнала переноса для каждого разряда.

Определим функции, реализуемые специальными схемами для разрядов.

Введем две вспомогательные функции (для удобства) рис. 5.6.

1. Функция генерации: γi=ai·bi, которая принимает единичное значение, если перенос на выходе данного разряда появляется независимо от наличия или отсутствия входного переноса.

2. Функция прозрачности (транзита): βi=ai ˅ ai , которая принимает единичное зачение на выходе данного разряда появляется только при наличии входного переноса. Но поскольку при ai=bi=1 перенос формируется при γi=1, то функцию транзита можно представить: βi=ai ˅bi. Теперь выражение для сигналов можно представить так – CRi=γi˅βi·CRi-1, на основе которого получены равенства для разрядов 0,1 и 2.

На рис. 5.6 – представлены все неравенства.

На основе этих уравнений построены специальные схемы для сумматора трехразрядного для формирования переносов (рис. 5.7).

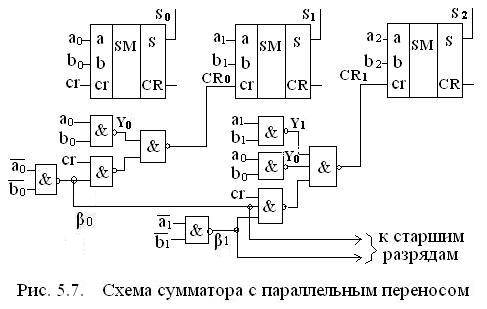
Из схемы видно, что время задержки суммирования складывается из:

- времени формирования функции βi раном τ,

- времени CR равном 3τ

- времени задержки одноразрядного сумматора SM равном (4÷5)τ.

Итого суммарная задержка составляет (7÷8)τ, причем она не зависит от числа разрядов. Фактически это не совсем точно, поскольку с ростом числа разрядов увеличивается нагрузка на элементы. Например, на элемент, формирующий β0 – подключен 1 элемент, β1 – подключаются 2 элемента и т. д. А это приводит к росту задержки τ этих элементов, и начиная с определенного числа разрядов, сумматор начинает терять преимущества параллельного переноса по быстродействию.

Практически используются:

-сумматоры до четырех разрядов – последовательный перенос,

-сумматоры до восьми разрядов – параллельный перенос.

§ 5.4 Двоично-десятичные сумматоры.

Для операций над десятичными числами каждая цифра от 0 до 9 представляется двоичной тетрадой, после чего операции над десятичными числами производятся над тетрадами, как над двоичными числами.

Такое представление десятичных чисел получило название двоично-десятичного кода, отнесенного к классу взвешенных кодов. Очевидно, что для представления десяти цифр необходим четырехразрядный двоичный код. На рис. 5.8 представлена таблица соответствия десятичных цифр двоичным тетрадам.

Из таблицы видно, что тетрады двоичного кода, начиная с 1010 и до 1111 не используются (будем считать их запрещенными), следовательно при суммировании тетрад с 0000 до 1001 в итоге могут появиться запрещенные тетрады, что приведет к неверному результату и подстверждает пример суммирования, рассмотрены на рис. 5.8, из которого видно, что тетрада 1110 запрещенная, оказалась с избытком 10 и потребовала коррекции – вычитания этого избытка 10, представленного в доп. коде и переноса 1 в следующую (старшую) тетраду. На основе этих рассуждений можно построить сумматор для подобных сложений одноразрядных десятичных чисел, представленных двоичными тетрадами.

Такой сумматор. его УГО и наращивание его разрядности приведены на рис.5.9 а), б), и в) соответственно.

Из схемы видно, что если в результате суммирования получается разрешенная тетрада, то а выходе логической схемы формируются нули, и следовательно, разряды «bi» SM2 (2) влияния на разряды аi, поэтому результат суммирования в SM2(1) формируется без изменения.

Если же образуется запрещенная тетрада, логическая схема на ее основе сформирует коррекционную комбинацию и результат в SM2 (2) будет скорректирован.

При вычитании двоично-десятичных чисел используются преобразователи числа В (вычитаемого) в дополнение до 9 (получение обратного кода значения вычитаемой тетрады) на основе соотношения |W=9-B|, где W – дополнение, В – вычитаемое.

Фукционирование тактов преобразоветелей описывается таблицей дополнений, представленной на рис. 5.10 а), а соединение преобразователя с десятичным сумматором на рис. б).

где: SUB-(Substract) – вычитание,SUB=0 – сложение, SUB=1 – вычитание, Z – сигнал установки нулевого значения на выходе блока. Z=0 – на выходах «0».

§ 5.5 Блоки для логических операций

В составе процессора ЭВМ (в ALU) есть блоки, выполняющие до 16 логических операций. Общая структурная схема блоков приведена на рис. 5.11 а).

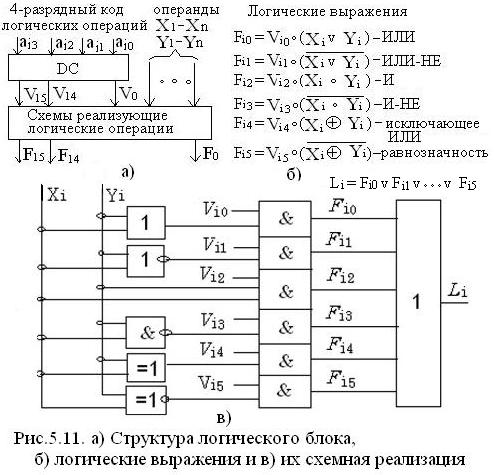
Пример построения схемы, реализующей 6 логических операций, приведенных на рис. 5.11 б), показан на рис. 5.11 в). Каждая из функций Fi,выполняемая определенным логическим элементом: ИЛИ,ИЛИ-НЕ,И и т.д. или их совокупностью.

Ко входам X_i и Y_i подключаются соответствующие выходы (разряды) буферных регистров ALU (о котором будет сказано ниже) RGA и RGB,а ко входам V_io ÷V_is- соответствующие выходы дешифратора команд ДС.

Типов логических блоков может быть много. В качестве примера на рис. 5.12 приведена другая схема блока, для одного разряда выполняющая четыре логические операции.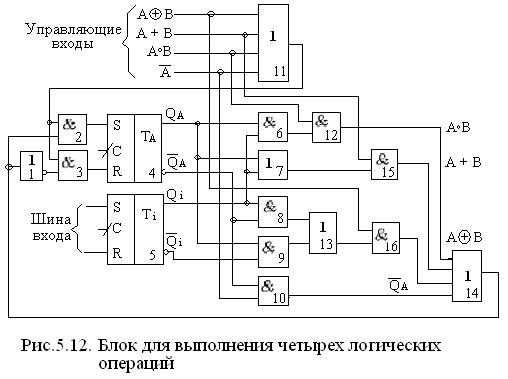

Т_А(эл-т 4)-является триггером (разрядом) регистра сумматора ALU-RGSM (аккумулятора) а Т₁(S)-триггер (разряд) входного регистра ALU-RGB.

Остальные элементы составляют логический блок. Блок выполняет 4 операции: конъюкции, дизъюкции, арифметического сложения, сложения по

mod2 и инверсии между разрядами. Отличительная особенность блока – все операции могут выполняться одновременно и поразрядно между Т_А и Т₁ , но результат записывается в один триггер (в нашем случае в Т_А) поэтому одновременная подача управляющих сигналов недопустима.

Выбор операции осуществляется подачей «1» на соответствующий управляющий вход блока.

Например: реализовать операцию Ai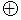Bi подачей на него «1».

Тогда: сигналы Q_А и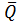_i проходят на конъюнктор (9), а 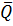_А и Qi – на элемент (8), с выходов элементов (8) и (9) результаты конъюнкции подаются на ИЛИ (13), на выходе которого получается результат:

Q_А ·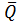_i + 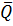_А · Qi = A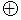iBi.

Этот результат при подаче «1» на вход элемента (16) пересылается в (14) и далее записывается через элемент (2) в Та (4), где и фиксируется.

Другие операции выполняется аналогично. Блок может быть расширен для выполнения и других операций.

Глава 6. Арифметико – логические операции ЭВМ (ALU). Основные характеристики ALU.

ALU – функционально законченный узел процессора ЭВМ, предназначенный для выполнения арифметических операций по обработке информации.

Основные операции, выполняемые ALU:

- Арифметические (все они сводятся к сложению), до 50% от всех выполненных операций.

- Логические (до 16 операций – до 45% от всех выполнений).

- Остальные 5% - операции управления.

Основные связи ALU в составе процессора показаны на рис 6.1.

ALU – основные части которого сумматор и комбинационная логическая схема (блок логических операций) имеет 2 группы входов (портов) Вх1 Вх2 для приема данных (операторов) и 2 группы выходов: Вых1 – выход результата операции, выполненной ALU (сумматором) или логическим блоком. Вых2 – выход осведомительной информации (признаков) результата операции: переполнение разрядной сетки, знак результата деления на «0» и т.д.

Эта информация используется для коррекции управляющих сигналов в блоке управления.

RG1 и RG2 – регистры (их иногда называют буферными) для приема операторов из памяти ЭВМ.

RG SM – регистр сумматора (его чаще называют аккумулятором) для приема из сумматора или блока логических операций результата операции и передачи его либо в RG1 (RG2) либо в память ЭВМ.

SM – сумматор.

6.1 Классификация ALU.

ALU классифицируются по нескольким признакам:

1. По способу действия над операциями:

- последовательные, когда операнды представлены в последовательном коде и операции над ними выполняются разряд за разрядом.

- параллельные, когда операнды представлены в параллельном коде и операции выполняются над всеми разрядами одновременно.

2. По способу представления чисел:

- ALU для чисел с фиксированной точкой.

- ALU для чисел с плавающей точкой.

- ALU для десятичных чисел.

3. По характеру использованных блоков ALU:

- Блочные, когда операции над числами с фиксированной и плавающей точкой, с десятичными числами и алфавитно-цифровыми полями выполняются в отдельных (специализированных) блоках. Обладают высоким быстродействием. Т.к. блоки могут работать параллельно.

- Многофункциональные ALU, когда все операции выполняются одними и теми же блоками, которые коммутируются нужным образом.

ALU управляются сигналами, инициирующие выполнение определенных микроопераций. Последовательность таких сигналов определяется кодом операции и осведомительными сигналами из RGпр по результатам предыдущей операции.

Проектирование ALU в основном состоит в:

- Выборе кодов для представления данных

- Определении алгоритмов выполнения операций

- Выборе структур операционных блоков и набора микроопераций, реализуемых ими

- В объединении блоков в один многофункциональный узел – ALU.

6.2 Языки описания вычислительных устройств.

ЭВМ – одна из самых сложных технических систем, описание структуры и функционировании которой производится на различных уровнях ее детализации. Каждому уровню описания соответствуют определение средства.

Потребность в таких формализованных средствах описания диктуется не только потребностями современной методологии изучения сложных систем но и потребностями моделирования проектных решений при создания системы, автоматизации проектирования и т.д.

Для формированного описания часто используют различные «языки описания», например, такие, как показаны на рис 6.2.

В нашем курсе рассматриваются в основном узлы системы, поэтому чаще всего используется язык микроопераций, который иногда называют регистровым или языком регистровых передач. Несколько примеров использования этого языка приведены на рис 6.3.

Пояснение: например слово –число Х₁₅[0-n]: здесь Х₁₅ – идентификатор – это произвольная последовательность букв и цифр, начинающаяся с буквы. [0-n] – разрядный указатель номеров разрядов.

Определения:

1. Элементарная операция, выполняемая за один тактовый интервал – называется микрооперацией.

2. В некоторые тактовые интервалы могут параллельно выполняться под действием управляющих сигналов несколько микроопераций. Совокупность таких операций называют микрокомандой.

3. Последовательность микрокоманд, обеспечивающая выполнение операции (например, сложение 2х числе) называют микропрограммой операции.

Микрооперация – это преобразование над операндами: один или несколькими, может быть одноместной или многоместной, описывается микрооператором (рис 6.3. пункт 4) и сопровождается меткой.

Аналогично описание и микрокоманды, представляющее собой метку и раздельную запятыми последовательность микрооператоров.

Обычно даже простые операции выполняются за несколько тактов. Например, микрокоманда – принять адрес в RG – адреса выполняются за два такта:

1. Уст.0 RGA: RGA:=0

2. Пр.А2: RGA:=RGK[A2]

Здесь: Уст.0 – обозначение управляющего сигнала для обнуления RGA.

Пр А2 – сигнал приема (записи) адреса А2 из регистра команды RGK.

Микропрограмма может быть в виде графа, в котором вершины соответствуют микрокомандам.

6.3 ALU для сложения (вычитания) чисел с фиксированной точкой.

В ALU операция сложения сводится к арифметическому сложению чисел, представленных в прямом или дополнительном кодах. Обратный код применяется редко, поскольку имеет 2 представления нуля +0 и -0, что затрудняет анализ результатов операции. Алгоритм операции сложения определяется типом применяемых кодов.

Функциональная схема ALU сложения (вычитания) приведена на рис 6.4.

Управляющие сигналы вырабатываются управляющим блоком в соответствии с кодом операции. Каждый управляющий сигнал идет по своему тракту: например, в RG1 может поступать 4 типа сигналов:

- Сигнал обнуления регистра

- Сигнал записи кода операнда из BDIO

- Сигнал выдачи кода с прямых выходов регистра

- Сигнал выдачи кода с инверсных выходов (при инвертировании кода)

Работа ALU.

Из оперативной памяти ЭВМ по шине BDIO поступают команды А и В, первое слагаемое (или уменьшаемое) в RGB, второе слагаемое в RG1. RG1 и RGA имеют прямую и инверсную связь для передачи кода операнда, прямую при сложении, инверсную при вычитании. Вычитание производится по формуле (А+¬В) где ¬В значение операнда В в обратном коде. К результату прибавляется +1. Результат суммирования (или вычитания) передается в RGSM и далее по шине BDIO в память.

При сложении двоичных кодов, включая и их знаковые разряды следует учитывать следующие правила:

1. Если возникает перенос из знакового разряда суммы при отсутствии переноса в этот разряд, или возникает перенос в знаковый разряд при отсутствии переноса из него, то имеется переполнение разрядной сетки соответственно при отрицательных и положительных суммах.

2. Если нет переносов из знакового разряда и в знаковый разряд суммы, или есть оба эти переноса, то переполнение разрядной сетки отсутствует и

- При «0» в знаковом разряде суммы положительная

- При «1» - отрицательная

На входы RGпр поступают:

- Значения всех разрядов сумматора СМ[0] и CM[1÷n-1]

- Перенос из знакового разряда Пн CM[0]

- Перенос в знаковый разряд Пн CM[1]

В результате этого, после выполнения операции в спец. Комбинационной схеме (на рис 6.4 – отсут-т) формируются признаки по соответствующим соотношениям показанным на рис 6.5.

На рис 6.6 приведена временная диаграмма работы ALU при сложении (вычитании) чисел с фиксированной точкой.

Из диаграммы видно, что сложение выполнено за 5 тактов, а вычитание за 6 тактов с добавлением +1.

6.4 Методы умножения двоичных чисел.

В ЭВМ операция умножения сводится к операции сложения двух чисел и сдвигу разрядов. Могут применяться 4 основных метода умножения. Примеры умножения приведены на рис 6.7.

Выводы по методам умножения.

1 метод.

1. После каждого сдвига множимого выполняется операция сложения.

2. Операция умножения состоит из n-циклов (n-разрядность множителя)

3. ALU при этом методе должно иметь:

- Регистр множителя (n-1) разрядный

- Сумматор и регистр сумматора 2(n-1) – разрядные.

Метод практически не применяется из-за большой разрядности регистров и сумматора.

2 метод.

1. Выравнивание суммы частных произведений по старшим разрядам.

2. Младшие разряды произведения по мере их формирования можно перемещать в освободившиеся разряды множителя, поскольку далее не используются, а старшие – записать в RGSM. И результат снимать с двух регистров. Метод часто применяется вследствие необходимости одинарной длины разрядности регистров буферных и сумматора.

3 метод.

1. Сумматор и RGSM необходим 2(n-1) – разрядности.

2. Последовательность действий в цикле определяется старшим разрядом множителя.

Метод применяется в некоторых ALU, так как позволяет без дополнительных цепей сдвига выполнять деление чисел, в то время как во 2м методе для деления необходимы цепи сдвига в регистре множимого (при делении – частного) и в сумматоре частичных произведений (разностей при делении).

4 метод.

1. Необходимы двойные разрядности регистра сумматора и сумматора.

2. При делении чисел требуются цепи сдвига в регистрах.

3. Сумма частичных произведений неподвижна, поэтому можно совмещать во времени операции сдвига сложения.

В заключение следует отметить, что выбор метода умножения определяется соотношением затрат оборудования на цепи сдвига, разрядности и быстродействием.

6.5 ALU для умножения чисел с фиксированной точкой.

Применяется второй метод. Рис 6.8.

Алгоритм умножения

1. Берутся модули от сомножителей.

2. Исходное значение SM частичных произведений приравнивается к нулю.

3. Если цифра множителя в разряде равна «1» то к сумме частичных произведений прибавляется множимое, если «0» - не прибавляется.

4. Производится сдвиг суммы частичных произведений вправо на один разряд.

5. Пункты 3 и 4 выполняются для всех разрядов множителя начиная с младшего разряда

6. Произведению присваивается «+» если знаки сомножителей одинаковы и «-» в противном случае.

Работа ALU.

В RG1 принимается множимое, RGB – обнуляется, в сч. Циклов (на схеме не показан) заносится число разрядов множителя, в RGB заносится множитель. Далее идет процесс умножения: в зависимости от значения младшего разряда множителя 0 или 1 к частному произведению прибавляется 0 или множимое соответственно.

Полученная сумма в RGSM со сдвигом на разряд вправо передается в RGB. Одновременно множитель сдвигается на разряд вправо путем косой передачи из RG2 в RG2’ и возврата в RG2.

Старшие разряды RG2’ при этом освобождаются и в них заносятся младшие разряды получаемого произведения.

Содержимое счетчика циклов с каждым перемножением уменьшается на 1 и при достижении в нем «0» процесс перемножения прекращается. В результате RGSM и RG2’ будут храниться соответственно старшие и младшие разряды произведения.

Особенностью умножения целых чисел является необходимость представления результата умножения двоичным словом. При этом число цифровых разрядов двойного слова 2N-1 на 1 больше числа 2n-2 цифровых разрядов произведения двух чисел, содержащих n-1 цифровых разрядов.

Поэтому, после перемножения чисел надо результат сдвинуть на разряд вправо, для правильного его расположения в разрядной сетке формата двойного слова. После сдвига результат операции передается на шину данных BDIO.

Умножение целых чисел со знаками, представленных в прямом и дополнительном кодах производится с применением модифицированного сдвига суммы частичных произведений.

6.6 О применении прямого, обратного и дополнительного кодов при выполнении арифметических операций в сумматоре.

Общеизвестно, что в сумматоре ALU реализуется только операция сложения, назовем условно, положительных операнд (чисел).

Положительные числа во всех кодах совпадают. Отрицательные представляются в обратном и дополнительном кодах, причем в операциях вычитания знак вычитаемого автоматически изменяется на противоположный. Знаковый разряд и цифровая часть числа рассматриваются как одно целое и одинаково участвуют в операции. При сложении в обратных кодах перенос из старшего знакового результата поступает на вход переноса младшего разряда (циклический перенос), а при сложении в дополнительных кодах этот перенос не учитывается.

Для напоминания на рис 6.9 приведена таблица соответствия прямого, обратного и дополнительного кодов для отрицательных чисел и даны примеры операций с применением обратного и дополнительного кодов.

На рис 6.10 приведены примеры возможного переполнения разрядной сетки при сложении чисел с одинаковыми знаками и применения модифицированных кодов для обнаружения переполнения.

6.7 ALU для деления целых чисел с фиксированной точкой.

Деление чисел сводится к выполнению последовательности вычитания делителя, сначала из делимого, затем из образующихся частичных остатков и их сдвига. Фактически деление заменяется суммированием с применением дополнительных кодов.

Деление можно осуществлять двумя основными способами:

1. Деление с неподвижным делимым и со сдвигаемым вправо делителем. Способ основан на копировании ручного деления. (самостоятельно поделить 2 числа, записать алгоритм деления и построить структурную схему ALU для этого способа).

2. Деление со сдвигаемым делимым и неподвижным делителем. Схема ALU для такого способа приведена на рис 6.11.

Неподвижный делитель В в дополнительном коде заносится в RGA, делимое А, сдвигаемое влево относительно делителя В заносится старшими разрядами в RGB, младшими в RG2. Деление начинается со сдвига делимого А путем косой передачи его в RGSM (старшие разряды) и в RG2’ (младшие разряды), после чего делимое передается из RGSM в RGB и из RG2’ в RG2.

Далее в SM происходит вычитание делителя (в RGA), образуется частичный остаток (путем подсуммирования +1) и цифра частного (1 если остаток >0 и 0 если остаток <0) заносится в освободившийся после сдвига А разряд RG2.

При этом если остаток <0, то его значение восстанавливается до предыдущего значения.

Алгоритм деления приведен на рис 6.12.

Недостаток способа: нужен дополнительный такт для восстановления остатка, поэтому иногда применяются способы деления без восстановления остатка.

Суть деления с восстановлением частичного остатка заключается в следующем:

Если при делении в результате вычитания делителя из делимого (частичного остатка) выясняется, что делимое или очередной частичный остаток оказались больше или равны делителю, то в очередной разряд частичного остатка заносится «1» и полученный частичный остаток сдвигается влево на один разряд.

Если же выясняется, что после вычитания делителя частичный остаток оказался меньше делителя, то в очередной разряд частного заносится «0», к полученному остатку прибавляется делитель, чтобы восстановить частичный остаток до вычитания, после чего результат прибавления сдвигается влево на один разряд. Описанные процессы продолжаются до получения n-разрядного частного. Такой метод и называется делением с восстановлением остатка на рис 6.13 приведен пример подобного деления.

Примечание. Часто в ЭВМ используется деление без восстановления остатка. Суть его в следующем:

Если результат вычитания делителя из делимого получен отрицательный, то частичный остаток не восстанавливается путем прибавления делителя, а на следующем шаге деления вместо вычитания делимого производится его прибавление к частичному остатку. Если результат при этом остался отрицательным, то в очередную цифру частного записывается «0» и на следующем шаге так же выполняется сложение. Если результат после сложения положительный то в разяряд частного записывается «1» и на следующем шаге производится вычитание.

6.8 Операции над числами с плавающей точкой. Представление чисел в ЭВМ.

1. При представлении чисел с фиксированной точкой, точка ставится в определенном месте относительно разрядов модуля числа в разрядной сетке. Рис 6.14

· точка перед старшим разрядом.

Здесь при переполнении разрядной сетки (при потере младшего разряда) погрешность не превышает величину 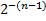. Метод применяется редко.

· Точка перед младшим разрядом.

Здесь модуль только целое число. При занесении числа в ячейку превышающего число 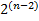теряется старший разряд и погрешность может достигнуть 100%. Например, 1111₂ (15₁₀) при потере старшего разряда становится 0111₂ (7₁₀).

2. Числа с плавающей точкой представлены иначе. Рис 6.14 п.2.

Порядок P числа может быть как положительным, так и отрицательным. Числа с плавающей запятой могут быть представлены в форматах с основанием 2, 8, 16 и двоично-десятичном.

Нормализованным числом принято считать число, у которого старший разряд мантиссы не равен нулю. ЭВМ автоматически нормализует число.

Например: получен результат, в котором r-старших разрядов мантиссы равны 0. Нормализация заключается в сдвиге мантиссы q на r-разрядов влево и одновременным умножением порядка P на r единиц. При этом в младшие освободившиеся разряды мантиссы записываются нули.

После такой операции число не меняется, а условие нормализации будет соблюдено. Поскольку арифметические действия над числами с плавающей точкой требуют отдельных операций над мантиссами и порядками, то операции над ними сводят к операциям над целыми положительными числами, применяя представление чисел со смещенными порядками. Для этого при записи числа в ячейку памяти к его порядку Р прибавляется целое число-смещение N=2^k, где K-число двоичных разрядов, используемых для расположения модуля порядка в разрядной сетке. Тогда смещенный порядок есть Р_см = P+N, который всегда будет положительным, причем для его представления надо такое же число разрядов, как и для модуля Р.

Особенность Р_см в том, что если P’ > P” то и для смешенных верно Р_см’ > Р_см”. Это говорит о том, что смещение порядков не влияет на операции над числами.

6.9 Сложение и вычитание чисел с плавающей запятой.

Сложение и вычитание чисел производится на формуле (в предположении что X>Y) приведенной на рис 6.15.

Используемая разрядная сетка показана на рис 6.15(г).

Алгоритм сложения и вычитания.

1. Производится выравнивание порядков слагаемых Х и Y: порядок меньшего по модулю числа принимается равным порядку большего числа, а мантисса меньшего сдвигается влево на число S-ичных разрядов, равное разности порядков.

2. Производится сложение (вычитание) мантисс и получается мантисса суммы (разности) чисел X и Y.

3. Порядок суммы (разности) принимается равным порядку большего числа.

4. Полученная сумма (разность) нормируется. Арифметические действия над порядками и мантиссами выполняются либо отдельными устройствами, либо последовательно одним устройством, например, ALU рассмотренным ранее.

Операция сложения (вычитания) состоит из этапов:

1. Прием операндов X и Y

2. Выравнивание порядков со сдвигом мантисс

3. Сложение (вычитание) мантисс

4. Нормализация результата

Структурная схема ALU для сложения (вычитания) чисел с плавающей точкой приведена на рис 6.16.

Работа ALU.

1. Прием операндов. Прием первого слагаемого (уменьшаемого) X, фиксация знака в триггере Т_ЗН, установка RGA в «0». Прием второго слагаемого (вычитаемого) Y в RG3, фиксация знака Т_ЗН , установка RGB в «0».

2. Операции над порядками. Значения порядков из разрядов операндов α₁÷α₇ регистров RG1 и RG3 подаются в RGC и RGD соответственно. Далее в блоке обработки порядков происходит их сравнивание по результатам которого: мантисса с меньшим по модулю порядком сдвигается влево на число разрядов, равное разности порядков. За порядок результат операции сложения (вычитания) мантисс принимается больший из порядков.

При сравнении порядков возможны 5 случаев их соотношения и соответствующих операций.

1. P_X – P_Y > m, где m – число разрядов мантиссы числа Х. за результат операции принимается слагаемое Х, так как при сдвиге мантиссы слагаемого Y все ее разряды примут нулевое значение.

2. P_Y – P_X > m, где m – число разрядов мантиссы числа Y. За результат операции принимается слагаемое Y по той же причине.

3. P_X – P_Y = 0, - производится суммирование мантисс числа Х и Y.

4. P_X – P_Y = K₁, (K₁ < m) – мантисса числа Y сдвигается на K₁ разрядов.

5. P_X – P_Y = K₂, (K₂ < m) – мантисса числа Х сдвигается на K₂ разрядов.

Процесс сдвига мантисс заключается в следующем: В счетчик циклов СТЦ из блока обработки порядков заносится число разрядов (К₁ или К₂) на которое необходимо сдвинуть. Далее, по мере сдвига мантиссы содержимое счетчика уменьшается и по достижении содержимого счетчика СТЦ = 0. Сдвиг прекращается.

Полученные модули мантисс хранятся в RG1 и RG3, их знаки в триггерах знака, а принятый порядок в RGCT1.

3. Сложение мантисс.

· При одинаковых знаках операндов. Модули мантисс передаются в RGA и RGB без изменения и складываются в сумматоре SM. Если окажется, что в разряде SM[7] = 1, то возникло переполнение разрядной сетки, поэтому сумма сдвигается на разряд вправо, а порядок Р увеличивается на 1: т.е. в RGCT1:= RGCT1+1.

Если после этого в RGCT1[α₀] = 1, то возникло переполнение порядка, вырабатывается сигнал прерывания вычислительного процесса.

Если переполнения порядка нет, то в RGSM[α₁÷α₇] заносится порядок из RGCT1, в RGSM[α₀] – знак мантиссы из сх.зн., а в RGSM[α₈÷α₃₂] мантисса суммы.

· При разных знаках операндов. Отрицательная мантисса передается в RGA или RGB в обратном коде, производится суммирование в SM с положительной мантиссой с дальнейшим подсуммированием +1 к результату. Знак результата фиксируется в соответствующем триггере знака. Если полученный результат нормализованный, т.е. в SM[0] ≠0 то в RGSM заносится:

- Знак результат в RGSM[α₀]

- Порядок из RGCT1 в RGSM[α₁÷α₇]

- Модуль мантиссы результата из SM в RGSM[α₈÷α₃₂].

Если результат нормализован, т.е. SM[α₈,α₉,…] = 0 и нет исчезновения мантиссы, т.е. SM[α₈÷α₃₂] ≠ 0, то производится нормализация сдвигом мантиссы влево с одновременным уменьшением порядка: т.е. RGCT1:=RGCT1 -1.

При отрицательном переполнении порядка, т.е. при RGCT1[0]формируется признак исчезновения порядка (т.е. результат = 0). Если нормализация происходит без исчезновения порядка, то формируется результат в RGSM и кодов знака, порядка и мантиссы.

Примечание: в операциях с числом с плавающей точкой сложение и вычитание выполняется приближенно, т.к. при выравнивании порядков может произойти потеря младших разрядов одного из операндов. Погрешность в этом случае всегда отрицательна и может доходить до «1» младшего разряда. Поэтому применяется округление результат, для чего используется дополнительный разряд в SM, в который после суммирования добавляется «1».

6.10 Умножение чисел с плавающей точкой.

Производится по формуле, приведенной на рис 6.15 б. Из формулы видно, что при перемножении:

- Порядки складываются

- Мантиссы перемножаются

- Произведение нормализуется и

- Ему присваивается знак «+» если знаки сомножителей одинаковы и «-» в противном случае.

Если одна из мантисс равна «0» произведение принимается равным нулю и переполнение не производится.

Если при суммировании порядков возникло переполнение порядка и его знак отрицательный, то результат умножения принимается равным «0» т.к. произведение окажется меньше разрядной сетки.

Если возникло переполнение порядка со знаком «+», то может оказаться, что после нормализации результата перемножения мантисс переполнение исчезнет. Поэтому в этом случае факт переполнения запоминается до окончания нормализации результата.

Как уже упоминалось, операции над порядками могут выполняться в разных блоках ALU или в одном:

1. В сумматоре SM, в котором выполняются операции перемножения мантисс – последовательно: сначала над порядками, затем над мантиссами.

2. Операции над порядками в блоке логических операций, а над мантиссами в SM ALU.

Схема ALU для второго случая приведена на рис 6.17.

Назначения RG в схеме:

RG1 – для приема и хранения множимого А.

RG2 и RG2’ – для приема мантиссы множителя В и ее сдвига в процессе перемножения.

RG3 – для приема знака и порядка множителя В и последующего приема частных произведений из RGSM.

RGА – для передачи на сумматор мантиссы множимого А, порядка его КПС блока логических операций и знака в Т_ЗН.

RGВ – для передачи в SM частичных произведений порядка множителя В в RGD блока логических операций.

RGSM – для приема частичных произведений из SM и последующего результата перемножения: знака, порядка и мантиссы.

RGCT1 – для хранения порядка результата.

СЦТ – счетчик циклов, используется при нормализации.

Работа ALU.

1. Прием операндов: прием множимого А в RG1, фиксация его знака в NPY? Установка RGA в «0». Прием множителя В: знака и порядка в RG3, а мантиссы В в RG2, фиксация знака Т_ЗН, установка RGВ в «0».

2. Передача порядков чисел А и В в RGС и RGD соответственно, их выравнивание в блоке логических операций со сдвигом соответствующей мантиссы в RG1 или RG2, фиксация принятого порядка в RGСТ1. (сдвиг осуществляется под управлением счетчика циклов).

3. Перемножение мантисс. Передача мантиссы множимого А в RGА и далее в сумматор SM. При значении первого разряда мантиссы множителя В в RG2 равного «1», мантисса числа А фиксируется в RGSM как первое частное произведение и передается в RG3. После этого мантисса в RG2 через RG2’ сдвигается влево на разряд и при значении этого разряда равном «1» процесс повторяется. Если же значение разряда равно «0», то частное произведение в RGSM сдвигается на разряд влево и передается в RG3. (без суммирования). Все повторяется для всех разрядов множителя В.

Окончательный результат фиксируется в RGSM: знак из Т_ЗН, порядок из RGСТ1 и мантисса из SM, далее из SM на шину BDI.

Таким образом логично сделать вывод – умножение чисел это процесс суммирования мантиссы множимого и частичным произведениями столько раз сколько разрядов в мантиссе числа В, т.е. процесс аналогичен перемножению чисел с фиксированной точкой.

6.11 Деление чисел с плавающей точкой.

Производится в соответствии с формулой приведенной на рис 6.15 в.

Общие замечания: при делении чисел с плавающей точкой обычно, мантисса частного равна частному полученного при делении мантиссы делимого на мантиссу делителя, а порядок частного равен разности порядков делимого и делителя. Частное нормализуется и ему присваивается «+» если знаки делимого и делителя одинаковы и «-» в противном случае.

Если делимое = 0, в частное записывается 0 без выполнения деления.

Если при вычитании порядков образовалось положительное переполнение или если делитель = 0 деление не производится и формируется сигнал прерывания процесса.

При делении нормализованных чисел с плавающей точкой может оказаться, что мантисса делимого много больше мантиссы делителя и тогда мантисса частного может образоваться с переполнением сетки, поэтому часто перед делением мантисс, нарушают нормализацию делителя сдвигом его на разряд влево. Тогда нарушения нормализации частного не происходит.

Деление мантисс как правило происходит аналогично делению чисел с фиксированной точкой. Отличие только в том, что делимое берется такой же длины, что и делитель.

Однако, учитывая то, что мантисса делимого выражается дробным числом, можно условно принять, что делимое имеет двойную длину с нулями в младшей его половине. В этом случае после сдвигов влево частичных остатков, освобождающиеся разряды заполняются нулями и следовательно деление можно выполнять в точности так же как деление целых чисел.

Схема ALU для деления чисел с плавающей точкой, выполняющего в одном SM. (деление: неподвижное делимое и сдвигаемый делитель) рис 6.18.

Операция деления начинается с приема операндов в RG1 и RG2, фиксация знаков в триггерах знаков Т_ЗН, передачи слагаемых порядков в RGА и RGВ из разрядов RG1[1÷7] и RG2[1÷7]. Далее вычисляется их разность путем сложения в SM прямого кода смещенного порядка Р_СМ делителя. Результат заносится в RGСТ1. Далее происходит деление мантисс аналогично делению чисел с фиксированной точкой.

Глава 7. Умножители, драйверы, синхронизаторы.

7.1. Умножители.

Вслед за успехами технологии изготовления ИС происходит переход от выполнения арифметических операций в ЭВМ с использованием последовательных комбинационных устройств (например сумматоров) к специализированным ИС, выполняющих операции аппаратными способами, что значительно увеличивает быстродействие ЭВМ.

Логика построения таких блоков чаще всего связана с традиционными алгоритмами выполнения операций.

Построение например блоков умножения (умножителей) двоичных кодов на основе суммирования частичных произведений, получаемых с применением конъюнкторов.

Рис 7.1.

Здесь частичные произведения А₀*B₀, В₀*А₁ и т.д. формируются конъюнкторами 1 – 4 (причем одновременно), а код результата сумматорами 5 и 6 (последовательно). Полученная схема умножения носит название матричного множительного блока (ММБ).

Используя такой подход логично синтезировать умножитель произвольной разрядности.

Пример: Пусть имеем 2 числа разрядности m*n.

А_m=a_m-1a_2юююф0 и B_n=b_n-1b_n-2…b₀

Перемножим два 4-х – разрядных числа А и В. Рис 7.2.

Из рассмотренного процесса перемножения в столбце М₂ чисел А и В логично сделать вывод: каждый из выделенных блоков должен: получить частичное произведение b₁a₁ (в блоке 1) и дополнительно прибавить, кроме переноса Р, полученного от сложения b₀a₁ в самом блоке, частичные произведения b₀a₂ и b₂a₀, полученных в соседних блоках 2 и 3, т.е. каждый блок должен реализовывать показанное на рис 7.2. соотношение М=А*В + С*D.

Следовательно в рассмотренную схему умножения двух 2-х – разрядных чисел (рис 7.1.) надо добавить еще два сумматора для прибавления к А*В слагаемых С*D.

С учетом сказанного на рис 7.3 приведена схема 4-х – разрядного умножителя.

Работа схемы очевидна и соответствует алгоритму умножения 4-х –разрядных чисел А и В.

4-х – разрядные сумматоры SM1, SM2 и SM3, используемые в схеме умножения на рис 7.3., построены на основе одноразрядных сумматоров, соединенных по схеме приведенной на рис 7.4.

Вывод: для построения множительно – суммирующего блока для n – разрядных чисел требуется: n­­² – конъюнкторов и n² одноразрядных сумматоров.

Максимальная длительность умножения t_умн есть сумма задержек сигналов в конъюнкторах для определения произведения b_j*a_i и задержки в цепочке передачи сигналов в матрице одноразрядных сумматоров т.е.

t_умн = t_k + (m+n-1)t_sm.

где t_k – задержка конъюнктора,

t_sm – задержка одноразрядного сумматора SM.

УГО умножителя показано на рис 7.4. б

Где Е – сигнал стробирования

MPL – Multiplir – матричный умножитель. Примеры выпускаемых умножителей:

Серия 1802: 8х8(17нс), 12х12 разр. Минск 32х32 (250нс) Hitachi 16х16 (5нс).

7.2. Последовательные умножители.

В последовательных умножителях вычисляются n+m – разрядное произведение:

P=A_n+B_m

Где A_n = a_n-1…a₁a₀ – множимое разрядности n.

B_m = b_m-1…b₁b₀ – множитель разрядности m.

Множимое А_n записывается в параллельном коде во внутренний регистр памяти умножителя, а разряды множителя B_m подаются на умножитель последовательно начиная с младшего разряда по мере умножения.

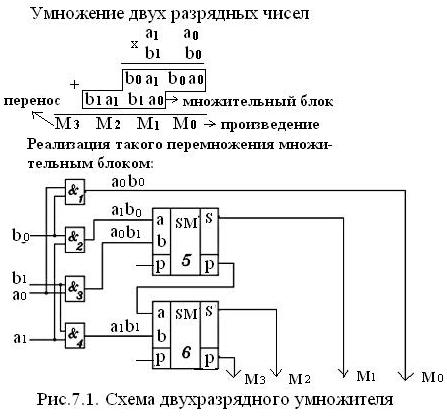
Из традиционного алгоритма умножения чисел известно, что умножитель должен иметь накапливающий сумматор, состоящий из n – разрядного комбинационного двоичного сумматора и сдвигающего регистра, который используется и в качестве аккумулятора старших разрядов суммы частичных произведений.

Схема накапливающего сумматора приведена на рис 7.5.а, работа которого очевидна.

В множителе применяются два типа триггеров (рис 7.5. б и в):

D-L – триггер и D-L/R – триггер с приоритетным входом сброса R. Их работа ясна из схемы.

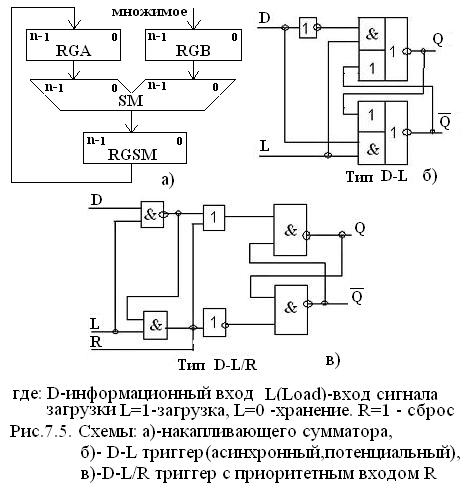
Схема умножителя и его УГО приведены на рис 7.6. а и б соответственно.

8 – разрядный регистр RG1 памяти умножителя для числа A₈ построен на D-L – триггерах (асинхронные, потенциальные), а 9 – разрядный сдвигающий регистр RG2 на D-L/R триггерах. Выход сумматора SM 9 – разрядный с учетом переноса.

Загрузка множимого A₈ в RG1 производится параллельно по сигналу ¬R=0, который одновременно сбрасывает RG2 в «0». Умножение числа А₈ на один разряд b^k множителя В₈ (его разряды поступают последовательно друг за другом) (к- номер разряда и такта) производится набором из 8 логических элементов И:

a_iхb^k = a_i*b^k

Пока поступают разряды b^k множителя, сдвигающий регистр RG2 работает в режиме синхронной (параллельной) загрузки (L=0). Эффект сдвига это время при передачи суммы из RG2 в сумматор SM обеспечивается подачей разрядов RG2 с весом на 1 больше на разряды сумматора, то есть разряды RG2 Q_КН с весом 2^К+1 подаются на входы сумматора SM – подаются b^k с весом 2^к.

Умножение выполняется за m+n тактов с выдачей произведения Р в последовательном коде с выхода Q₀ сдвигающего регистра RG2. Первые m – разрядов произведения выдаются при загрузке RG2 за счет эффекта сдвига при вышеупомянутой передаче из RG2 в SM, а остальные n – разрядов после подачи сигнала L=1, который переключает RG2 в режим сдвига под действием тактового сигнала ¬С.

Множитель В_m может иметь произвольную разрядность. УГО умножителя показано на рис 7.6. б. Пример серийно выпускаемого умножителя К555И9 (8 х 1 бит).

7.3. Драйверы. Шинные приемопередатчики.

Усилитель тока с большой нагрузочной способностью принято называть буферами или драйверами.

Многоразрядные драйверы с Z – состояниями выходов используются для подключения устройств к системной (внутренней) шине микро процессорных систем с помощью монтажное ИЛИ, к общим шинам других устройств. Также драйверы часто называются формирователями или шинными драйверами (Bus Driver).

Схема данного многоразрядного драйвера и УГО приведены на рис 7.7. Если каждый разряд многоразрядного драйвера управляется отдельным сигналом то его принято называть линейным драйвером.

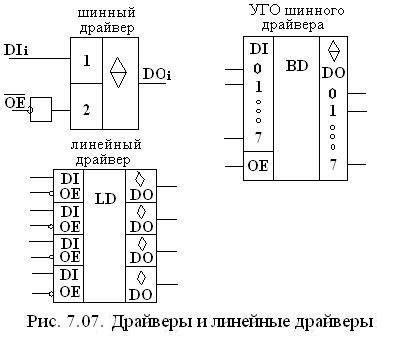
УГО – линейного драйвера приведено на рис 7.7. Он содержит 4 линейных формирователя. Шинные формирователи могут быть с открытым коллектором.

Шинные приемопередатчики.

Рассмотренные драйверы передают сигналы в одном направлении. Однако часто возникает необходимость передавать данные по одной шине в двух направлениях (противоположных), например, от процессора к памяти или внешнему устройству и наоборот.

Для этого применяются двунаправленные драйверы, которые называются приемопередатчиками (transceiver) схема и УГО которых приведены на рис 7.8 а и б.

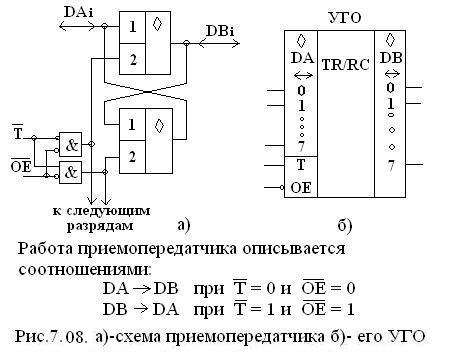
В остальных случаях выходы приемопередатчика находятся в Z – состоянии.

Глава 8. Синхронизация и прием внешних сигналов в ЭВМ.

8.1. Синхронизация в цифровых устройствах.

Синхронизация осуществляется генератором, сигналы С которого распределяются по всем частям устройства и разрешают прием и выдачу данных элементами памяти, упорядочивают во времени выполнение операций – это называется стробированием.

Тракт обработки данных можно представить чередованием комбинационных цепей (КЦ) и элементов памяти (ЭП), отражающего работу устройства при пространственном чередовании КЦ и ЭП (рис 8.1 а) и при последовательном выполнении операций в разных временных тактах на одно и том же оборудовании. (рис 8.1. б).

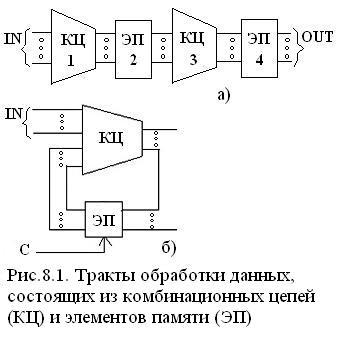
В КЦ – пути сигналов от входа к разным выходам могут быть неодинаковы, поэтому для расчета системы синхронизации надо оценивать задержки t_{кц min} и t_{кц max} для самого короткого и самого длинного путей прохождения сигналов.

Расчет параметров тактовых импульсов.

Основные соотношения параметров видны на временной диаграмме тактовых импульсов (рис 8.2) и приведены на (рис 8.3).

Период тактового сигнала Т есть сумма его длительности t_u и паузы t_П: T = t_u+t_П (рис 8.3).

Для надежной записи информации в элемент памяти (будем подразумевать синхронный триггер) должно соблюдаться условие:

t_u ≥ t_WC (t_WC – время срабатывания триггера, задается в его паспорте).

Триггер принимает новое состояние по истечении одной из максимальных задержек t₃⁰¹ и t₃¹⁰. Параметры t_WC и max (t₃⁰¹, t₃¹⁰) зачастую близки по величине, но иногда могут различаться в 2÷3 раза. Обозначим эту разность:

Δt_ТР = max (t₃⁰¹, t₃¹⁰ - t_WC)

После установки нового состояния триггера, сигнал с его выхода должен пройти через КЦ по самому длинному пути (t_{кц max}) плюс время предустановки следующего триггера t_C.

Тогда требуется пауза между импульсами должна быть: t_П ≥ Δt_ТР + t_{кц max} + t_C

Следовательно минимальный период синхросигналов есть: T_min = t_u+ t_П= t_WC+ Δt_ТР + t_{кц max} + t_C

А их частота: f_max = 1/T_min

В современных цифровых устройствах, работающих с высокой частотой, в расчетах параметров синхроимпульсов, приходится учитывать и время прохождения сигнала по линиям связи между элементами, т.е. учитывать топологию межсоединений. Поэтому начальное проектирование устройства является ориентировачным.

Также в расчетах учитывается и нестабильность частоты f генератора:

f = f₀(1±Δf) где Δf=δ/f₀

f₀ начальная частота, Δf – отклонения от номинала.

Ширина поля допуска ухода частоты от номинала составляет 2 Δf → (±Δf), следовательно изменение частоты не должно выходить за пределы этого поля.

Определенные требования предъявляются и к крутизне фронтов синхроимпульсов. Следует вспомнить природу о гонках по входу (рис 8.3 а). Необходимую крутизну фронта можно определить из соотношения: рис 8.3.

t₂-t₁ = (U_{пор 2} – U_{пор 1­})/K

где К – крутизна в В/нс.

Вред малой крутизны виден из рис 8.3 б, поступление С – сигнала (сдвиг слова) должно передавать состояние Т₁ триггеру Т₂. Допустим порог срабатывания у Т₁ (U_ПОР1) минимальный, а у Т₂ – максимальный (U_ПОР2). Тогда Т₁ переключится раньше чем сработает Т₂, который не сможет принять сигнал с выхода Т₁ и информация будет потеряна.

Есть еще такое вредное явление для бесперебойной работы устройства, как расфазирование синхросигналов. Синхросигналы обычно поступают в большое число элементов устройства от одного тактового генератора через систему распределения по пирамидальной схеме, состоящей порой из многих ярусов, что приводит к расфазированию, т.е. неодновременному приходу синхроимпульса к элементам из-за разброса задержек по линиям распределения. Это равносильно сокращению одних интервалов и удлинению других, что может привести к сбоям в работе устройства.

Есть несколько способов борьбы с расфазированием:

- Увеличение интервалов на выходе ГТИ, т.е. уменьшению частоты синхроимпульсов (потеря быстродействия)

- Применение специальных быстродействующих элементов в цепях разводки синхросигналов.

- Ограничение обменов данными между элементами, синхронизируемых отдаленными выходами схемы разводки.

- Тщательный подбор длин проводников при проектировании из топологии, введением задержек в линиях для выравнивания времен прихода синхроимпульсов.

- В современных БИС применяется специальные схемы коррекции временного поглощения синхросигналов. Схемы получили название Phase Locked Loops (PLLS).

В заключение отметим что в цифровых устройствах применяется однофазовая, двухфазовая и многофазовая синхронизация.

8.2. Однофазовая синхронизация.

Использует минимальное число синхросигналов обеспечивая высокое быстродействие и в тоже время сопровождается специфическими проблемами. Поскольку при однофазной синхронизации на все элементы устройства подаются во времени одни и те же сигналы, то в случае безинерционных элементов такая синхронизация была бы невозможной, так как в момент подачи синхроимпульса один и тот же элемент, например, одноступенчатый триггер, должен одновременно на входе принимать данные, а на выходе выдавать хранящиеся в нем, что невозможно.

В силу же инерционности элементов однофазовая синхронизация возможна даже для одноступенчатых триггеров но при соблюдения условия рис 8.4. (1):

t_WC≤t_U≤t_TPmin+t_КЦmin – (1)

где обозначены:

t_WC – время переключения триггера

t_U – длительность тактового импульса

t_TPmin – минимально необходимое время переключения последующего триггера

t_КЦmin - минимально необходимое время переключения комбинационной цепи

здесь имеется в виду, что после переключения триггера (t_WC) на входе комбинационной схемы появится новые значения данных, а по истечении t_КЦmin изменится сигнал на входе последующего триггера, но которое не должно быть воспринято им, иначе его состояние измениться повторно в одном и том же такте, что недопустимо.

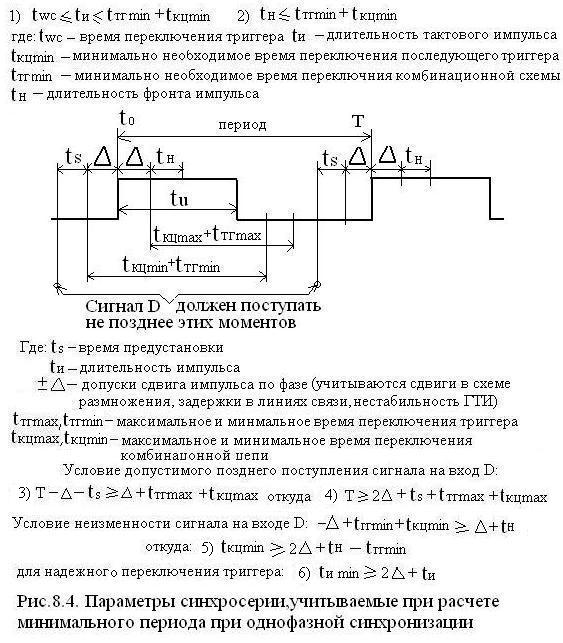
Отсюда вывод – необходимо строгое ограничение длительности тактового импульса t_U снизу и сверху. t_U должно быть таким, чтобы за это время переключился даже самый инерционный триггер и в тоже время информация не должна пройти через самый быстродействующий триггер.

К сожалению такому расчету длительности t_U препятствует отсутствие в паспортах элементов сведений о минимальных задержках их срабатывания. На практике однофазовая синхронизация чаще применяется в схема с триггерами имеющими динамическое управление или двухступенчатыми, у которых чувствительность ко входным сигналам сохраняется только в окрестностях фронта сигнала.

В этом случае должно соблюдаться условие рис 8.4. (2):

t_Н≤t_TPmin+t_КЦmin

где t_Н – длительность фронта синхросигнала С.

8.3. Расчет минимального периода синхроимпульсов для системы однофазовой синхронизации.

Предполагается использование элементов памяти – триггеров с прямыми динамическим управлением. Временная диаграмма и основные параметры тактовых импульсов приведены на рис 8.4.

t₀ – начало первого импульса

Т – период следования импульсов

±Δ – допуски сдвига фронта С – сигнала, здесь (t₀ – Δ) и (t₀ + Δ) – учтены:

Сдвиги в схеме размножения, задержки в линиях связи, нестабильность ГТИ.

t_S – время предустановки элемента,

t_В – время задержки элемента

t_TPmin и t_TPmax – минимальное и максимальное время переключения триггера

t_КЦmin и t_КЦmax - минимальное и максимальное время переключения комбинационной цепи

очевидно:

1. Чтобы сигнал на входе D триггера был неизменным в интервале предустановки t_S, он должен устанавливаться не позднее момента (t_S + Δ) для первого такта и момента

(Т – Δ - t_S) для второго такта.

2. Изменение информационного сигнала становится доступным не раньше момента (t_В + Δ)

для первого такта и момента (Т + Δ + t_В) для второго

3. Наиболее позднее появление информационного сигнала в интервале между импульсами С происходит в момент (Δ + t_TPmax + t_КЦmax), а наиболее ранее в момент

(-Δ + t_TPmin + t_КЦmin)

На основании этих утверждений можем записать:

a) Чтобы наиболее позднее поступление сигнала на входе D оказалось в допустимой области необходимо соблюдение условий (рис 8.4 (3) и (4))

(3) (Т – Δ - t_S)≥ (Δ + t_TPmax + t_КЦmax),

Откуда определяется период тактовых импульсов С:

(4) Т ≥ (2Δ+ t_S+ t_TPmax + t_КЦmax)

b) Для обеспечения неизменности сигнала на входе D в течение t_B необходимо соблюдения условия:

(-Δ + t_TPmin + t_КЦmin)≥ (t_В + Δ) откуда:

t_КЦmin≥(2Δ+ t_В- t_TPmin) (5)

c) Для надежного переключения триггера надо выполнить условие:

t_U ≥ (2Δ+ t_Umin) (6)

где t_Umin длительность импульса необходимая для переключения триггера.

Порядок определения вышеперечисленных параметров синхросерии:

1. Выбор t_U по выражению (6).

2. Выбор Т по условию (4)

3. Проверка выполнения условия (5)

Слагаемое 2Δ в выражении (5) отражает возможность запаздывания переднего и опережения заднего фронтов синхросигналов. Нарушение условия (5) может потребовать введения элементов задержек в соответствующие цепи, например, на выходах триггеров.

8.4. Двухфазовая синхронизация.

Двухфазовая или двухтактная синхронизация применяется в большинстве цифровых устройств, когда все схемы тактируются двумя взаимно разнесенными во времени последовательностями синхроимпульсов С1 и С2, вырабатываемых задающим генератором, и привязывают ко времени все процессы в устройстве.

Идею двухфазной синхронизации удобно рассмотреть на примере условной структурной схемы цифрового устройства на рис 8.5.в.

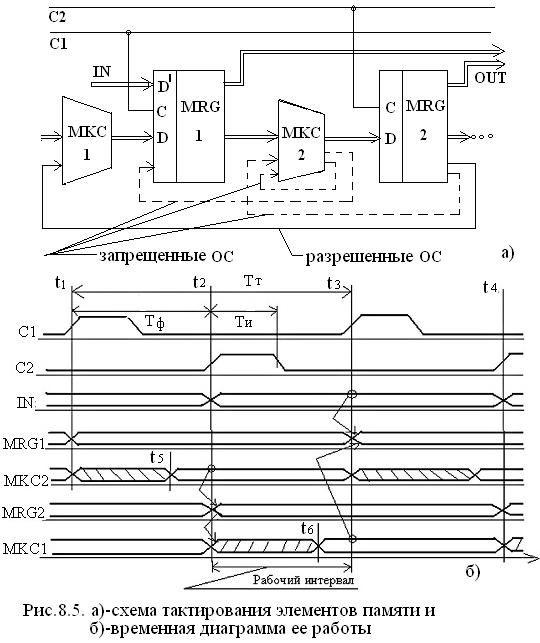
В ней все логические схемы разбиты на два класса:

- Схемы памяти (триггеры) объединенные в большие макрорегистры MRG1 и MRG2, которые срабатывают по синхросигналам С1 и С2.

- Комбинационные схемы объединены в макросхемы МКС1 и МКС2, в которые могут входить шифраторы, мультиплексоры, сумматоры и т.д., но отсутствуют триггеры и цепи обратной связи.

Каждая МКСi получает сигналы с выходов предыдущего MRGi, синхронизируемого С1 и подает результаты обработки на входы последующего MRGi+1 синхронизируемого С2.

Условимся, что сигналы, поступающие извне на вход D через синхронизаторы ввода внешних сигналов, меняются только по фронту С2.

На рис 8.5 б приведена временная диаграмма работы структурной схемы с двухфазной синхронизацией.

Временные параметры

Т_Т – период такта,

Т_Ф – фазовый период,

Т_И – длительность синхроимпульса.

Как правило двухфазная синхронизация является симметричной т.е. Т_Т = 2Т_Ф. суть процессов видна из временной диаграммы и стоит в следующем:

По фронту С1 сигнала в момент времени t₁ конъюнкторы макрорегистра MRG1 открываются и триггеры меняют свое состояние выходов в соответствии с входными сигналами из предыдущей комбинационной схемы.

Выходные сигналы MRG1 начинают обрабатываться схемой МКС2, переходные процессы в которой происходят до момента t₅ (заштрихованная область), но на входы MRG2 не попадают, т.к. С2 еще не открыл его входных конъюнкторов.

По фронту С2 открываются конъюнкторы MRG2 и сигналы с выхода МКС2 (с уже закончившимися переходными процессами) поступают в MRG2.

Переходные процессы в MRG2 (до момента t₆) не попадают на вход MRG1 через МКС1, поскольку конъюнкторы MRG1 открываются только по фронту С1.

И так в устройстве идет циклическая многоступенчатая обраб

Дата добавления: 2014-01-05