Закон Ома в комплексной форме для резистивного, индуктивного и ёмкостного элементов

А. Резистивный элемент. Ток через R .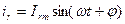

По закону Ома напряжение на R:

, (1)

где амплитуды тока и напряжения связаны соотношением: 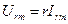(2).

Ток и напряжение на R совпадает по фазе.

Разделив (2) на 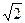, получим соотношение для действующих значений напряжения и тока для R:

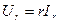(3)

В комплексной форме: и .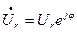

Тогда закон Ома в комплексной форме:

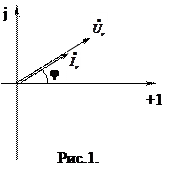
(4)

Б. Индуктивный элемент. При прохождении синусоидального тока 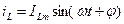через L, по закону электромагнитной индукции напряжение на L равно: 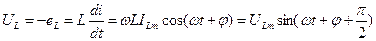(5)

Для амплитуд: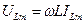(6)

Для действующих значений тока и напряжения (разделив для этого (6) на ):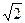

(7)

На рис.2А видно график мгновенных значений синусоидальных тока и напряжения на L.

Синусоидальный ток i_L отстаёт по фазе от синусоидального напряжения на π/2 – на четверть периода.

Величина X_L=ωL в (7) называют индуктивным сопротивлением (измеряется в Омах), а обратную величину b_L=1/ωL – называют индуктивной проводимостью (измеряется в Ом^-1 – См (сименсах)).

В комплексной форме: 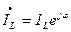и .

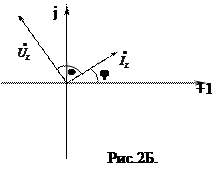
На рис.2Б показана векторная диаграмма для L. Вектор комплексного значения тока 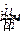отстаёт по фазе от вектора комплексного значения напряжения на четверть периода (π/2).

Закон Ома в комплексной форме для L:

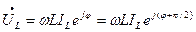(8)

или

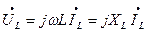(9)

Величина jωL=jX_L – называют комплексным сопротивлением индуктивного элемента, а обратная ей величина 1/ jωL=-jbL – комплексной проводимостью индуктивного элемента.

В. Ёмкостной элемент. Если приложить к конденсатору напряжение не меняющееся во времени, то величина заряда на пластине равна: q=Cu (на другой пластине заряд –q), где С – ёмкость конденсатора. Ток через конденсатор в этом случае не проходит.

Если же напряжение на конденсаторе меняется во времени 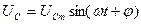, тогда заряд – меняется во времени, и, следовательно, через С пройдёт ток:

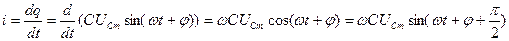(10)

Для амплитуд:

,

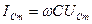для действующих значений:

(11)

X_C – называют ёмкостным сопротивлением (Ом);

b_C – называют ёмкостной проводимостью (См).

В противоположность индуктивности ёмкостное сопротивление уменьшается с увеличением частоты синусоидального тока. При постоянном напряжении сопротивление бесконечно велико.

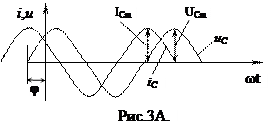
Из (5) и рис.3 видно, что для ёмкостного элемента синусоидальное напряжение U_C отстаёт по фазе от синусоидального тока i_C на π/2.

В комплексной форме: ; .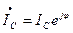

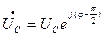Закон Ома для ёмкостного элемента в комплексной форме:

(12)

Величину 1/jωC=-jX_C – называют комплексным сопротивлением ёмкостного элемента, а величину jωC=jb_C – комплексной проводимостью.

Дата добавления: 2014-01-05