Д. Критерий устойчивости Гурвица

Дано характеристическое уравнение:

Составим таблицу Гурвица:

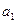
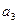
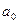
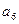
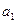
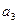
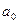
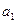
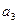
Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы 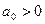, и все определ. Гурвица до 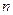включительно также были бы больше нуля.

Пример:

Система первого порядка:

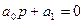
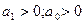: отрицат. корень

Система второго порядка:

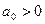(по определению)

Для систем 1-го и 2-го порядков необходимо и достаточно явление положительности всех коэффициентов.

Система третьего порядка:

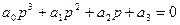
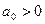(по определению)

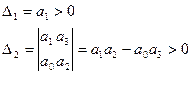
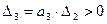(раскрываем по последней строке и последнему столбцу).

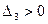при условии, что 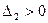только если .

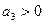Поэтому 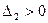в том случае, если .

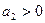Положительность всех коэффициентов является необходимым условием, но не достаточным.

Для того чтобы система 3-го порядка была устойчива, необходимо и достаточно, чтобы все коэффициенты были больше 0 и определитель 2-го порядка был бы больше 0.

Можно написать, что

Если 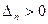, то система – на грани устойчивости.

(1) 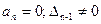САУ находится на грани апериодической устойчивости.

(2) САУ находится на грани колебательной устойчивости.

По критерию Гурвица также можно определить ПКУ. В дальнейшем рассмотри пример.

Пусть 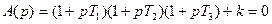(3.24)

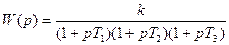
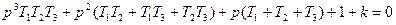(3.25)

Согласно критерию Гурвица система будет устойчива, если все коэффициенты больше нуля и определитель (по определению).

Произведение среднего должно быть больше произведения крайнего.

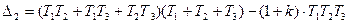(3.26)

Разделим (3.26) на :

(3.27)

Поделим правый сомножитель на 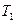, а левый умножим на .

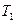(3.27’)

Заменив в (3.27’) знак неравенства на знак равенства, получаем:

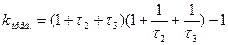(3.28)

При одинаковых Т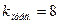

Система менее устойчива.

Из (3.28) видно, что ПКУ не зависит от постоянных времени, а от их отношений, соотношений между собой.

Рассмотрим 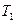при значениях 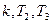(заданных), при которых система будет устойчива.

Пусть

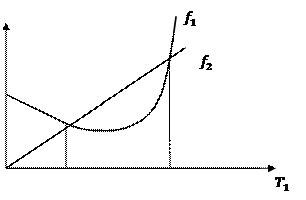
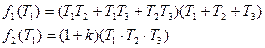
Система будет устойчива, где 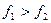(при малых значениях и при больших значениях).

Задача

Система неустойчива.

Критерий Гурвица работает как для разомкнутой системы, так и для замкнутой.

: по корням характеристического уравнения.

Система устойчива.

Е. Критерий устойчивости Найквиста.

Критерий устойчивости Найквиста позволяет определить устойчивость замкнутой системы по годографу разомкнутой.

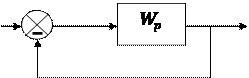
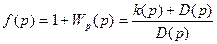(3.29)

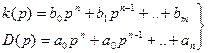(3.30)

Рассматриваем 3 случая:

(1) Разомкнутая САУ устойчива

(2) Разомкнутая САУ неустойчива

(3) Разомкнутая САУ нейтральна

(1) Разомкнутая САУ устойчива.

Дано:

(3.31)

Требуется доказать

(3.32)

Когда САУ будет устойчивая замкнутая.

Предположим, что замкнутая система устойчива.

Тогда

(3.33)

Док-во:

(3.32) справедливо при условии, если дано (3.31), если справедливо (3.33).

устойчивая

неустойчивая

Неудобно пользоваться функцией .

Вычтем эту единицу.

Тогда критической точкой окажется точка (-1,j0)

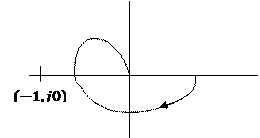Дано

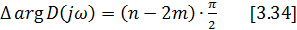
Доказать, когда

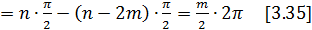
Доказательство ведётся от противного.

[3.32] будет справедлива в том случае, если дано [3.34], если справедлива [3.35]. Замкнутая система будет устанавливаться, если разомкнутая система не устойчива, если изменение вектора есть . Мы переходим к функции .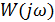

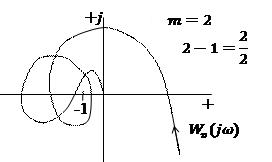
Если разомкнутая САУ неустойчива, переходя к годографу разомкнутой системы, то замкнутая САУ, если годограф разомкнут. САУ в положении в положении направления охватывает точку раз.

Замкнутая система устойчивости

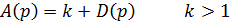
(3) Система нейтральна.

См. Нетушил

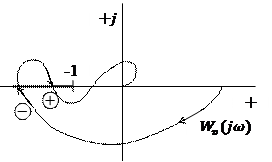Устойчивая система

Назовём переход годографа мнимой оси.

Сверху вниз – положительно, а снизу вверх – отрицательно.

Замкнутая система устойчива, если разность между положительным и отрицательным переходом равна .

Переход: -? (отрезок).

По критерию Найквиста легко определять предельный коэффициент усиления.

Например,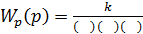

В разомкнутом состоянии система устойчива.

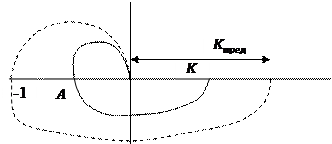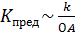
Дата добавления: 2014-01-05