Колебательное звено

Динамика процессов в колебательном звене описывается уравнением:

,

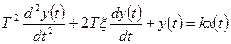где k - коэффициент усиления звена; Т - постоянная времени колебательного звена; 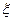- коэффициент демпфирования звена (или коэффициент затухания).

В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:

а) колебательное 0<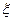<1;

б) апериодическое звено II порядка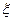>1;

в) консервативное звено 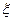=0;

г) неустойчивое колебательное звено 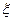<0.

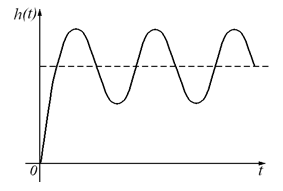
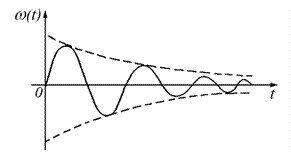
1. Переходная характеристика колебательного звена:

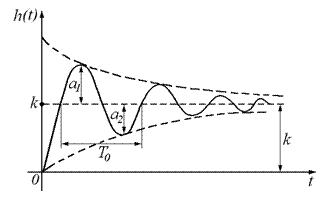
Амплитуды первых двух колебаний определяют величину -.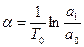

Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, чем меньше Т, тем быстрее устанавливаются переходные процессы.

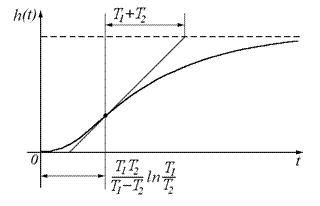
При x >1 колебательное звено называется апериодическим звеном второго порядка (последовательное соединение двух апериодических звеньев с постоянными времени Т₁ и Т₂).

t_c

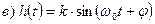, или можно записать так .

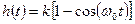Здесь w₀ – величина, обратная постоянной времени (); .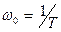

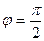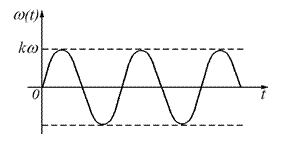
Такое звено в литературе называют консервативным звеном.

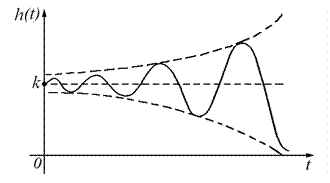
Все переходные характеристики будут колебаться вдоль величины k.

2. Импульсная переходная характеристика:

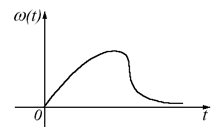
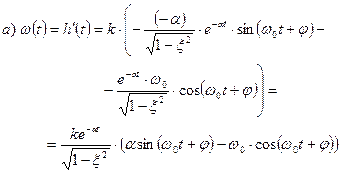
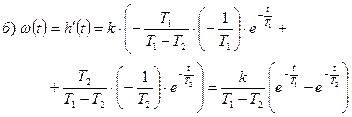
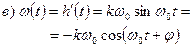
3.Передаточная функция:

4.АФХ:

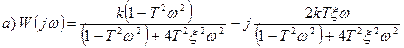
График АФХ будет выглядеть следующим образом:

Это характеристика для колебательного звена и для апериодического звена второго порядка.

Для апериодического звена - .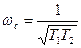

А в случае б) формула АФХ совпадает со случаем а).

-

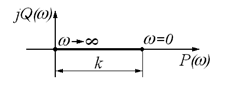
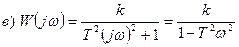- АФХ для консервативного звена.

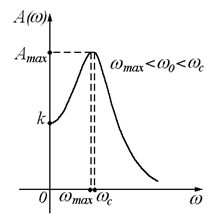5.АЧХ:

.

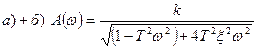АЧХ при частоте 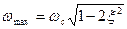имеет максимум (резонансный пик), равный

.

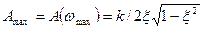Отсюда видно, что, чем меньше коэффициент x, тем больше резонансный пик.

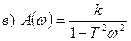
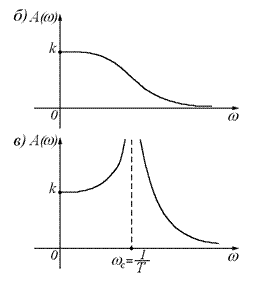Т.о., по графику АЧХ видно, что колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты; если частота гармонического входного сигнала близка к частоте собственных колебаний звена, то отношение амплитуды выходного сигнала к амплитуде входного больше передаточного коэффициента k.

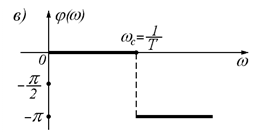
6.ФЧХ:

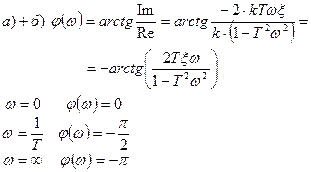
Для случая б) график будет аналогичным, только перегиб будет чуть меньше (штриховая линия на графике).

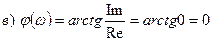
7.ЛАЧХ:

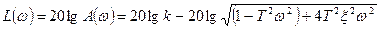, где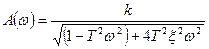

Асимптотическая ЛАЧХ колебательного звена:

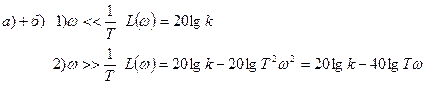
Определяем наклон на втором участке:

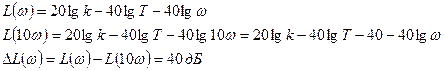
Шаблон к графику а) дается от 0 до 1 шагом в 0,1.

Консервативное звено:

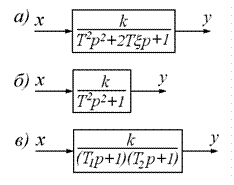
Структурная схема колебательного звена будет выглядеть следующим образом:

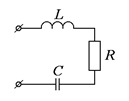
Примером колебательного звена является любая RLc- цепь.

Дата добавления: 2014-01-05