ЛЕКЦИЯ 7. При движении механической системы в потенциальных силовых полях полная механическая энергия системы сохраняется

При движении механической системы в потенциальных силовых полях полная механическая энергия системы сохраняется, т.е. система является консервативной.

Дифференциальные уравнения различных движений твердых тел

Вопросы лекции:

1. Дифференциальные уравнения поступательного и вращательного движений тела.

2. Дифференциальные уравнения плоскопараллельного движения тела.

3. Дифференциальные уравнения сферического движения тела (динамические уравнения Эйлера).

4. Определение динамических реакций опор вращающегося тела.

Дифференциальные уравнения всех типов движения твёрдых тел могут быть получены с помощью двух общих теорем динамики:

теоремы о движении центра масс

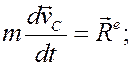
теоремы об изменении кинетического момента либо относительно центра масс

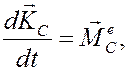
либо относительно неподвижного цент ра

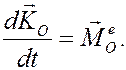
1. Дифференциальные уравнения поступательного и вращательного движений тела

а) Поступательное движение тела. При поступательном движении все точки тела движутся одинаково (траектории подобны, а скорости и ускорения точек равны в каждый момент времени). Поэтому для того, чтобы найти закон движения тела под действием приложенных внешних сил достаточно применить теорему о движении центра масс (1). В проекциях на оси декартовой системы координат получим

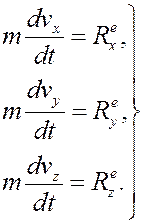
Уравнения (4) – это дифференциальные уравнения поступательного движения тела.

б) Вращательное движение тела. Здесь различают две задачи:

Ø решить вторую (или первую) задачу динамики без определения реакций опор, которыми обеспечивается неподвижность оси вращения тела;

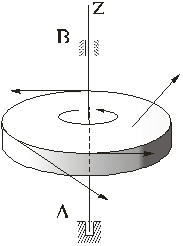
Ø решить вторую (или первую) задачу динамики и определить реакции опор.

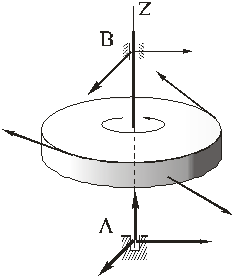
В первом случае достаточно применить теорему об изменении кинетического момента тела (3) в проекции на ось вращения. Обозначая ось вращения через z, учитывая, что для любого вращающегося тела

из теоремы получим

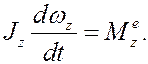
Уравнение (5) называют дифференциальным уравнением вращательного движения тела. С его помощью можно решить как первую задачу динамики (по заданному закону найти главный момент внешних сил), так и вторую задачу (по заданным внешним силам и начальным условиям найти закон вращения тела). Но так как реакции опор пересекают ось вращения z, то в (5) они не войдут 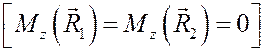и, следовательно, не могут быть найдены. Для их определения нужны дополнительные уравнения. Эта задача будет рассмотрена позже.

2. Дифференциальные уравнения плоскопараллельного движения тела.

Пусть тело совершает плоское движение под действием приложенных сил.

Т.к. плоское движение тела получается наложением поступательного движения вместе с полюсом на вращательное движение вокруг оси, проходящей через полюс перпендикулярно основной плоскости, то, принимая за полюс центр масс тела, используем

теорему (1) в проекциях на две оси Ox, Oy;

теорему (2) в проекции на ось Cz, перпендикулярную плоскости Oxy и проходящую через центр масс тела.

Получим в результате

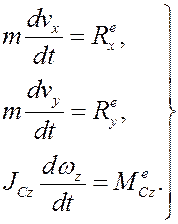
Уравнения (6) – это дифференциальные уравнения плоскопараллельного движения тела.

Рассмотрим примеры.

1) Однородный диск массы m и радиуса R вращается вокруг неподвижной горизонтальной оси с угловой скоростью 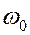. В некоторый момент двигатель отключают, и диск начинает вращаться с уменьшающейся угловой скоростью за счёт момента трения в подшипниках, который можно считать постоянным 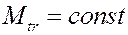. Определить, за какое время диск остановится?

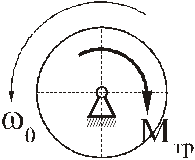
РЕШЕНИЕ. Диск совершает вращательное движение. Применим дифф. уравнение (5). Реакции шарнира и силу тяжести не показываем, т.к. их моменты относительно оси вращения равны нулю. Учитывая, что в данном случае (5) будет иметь вид

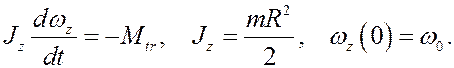
Интегрируя, получим

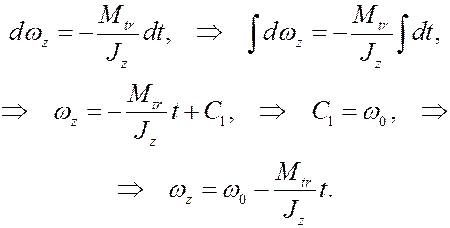
Учитывая, что в момент остановки 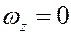, находим

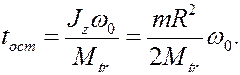
2) Колесо массы m и радиуса r установлено на горизонтальную плоскость и находится в покое. Радиус инерции колеса относительно центральной оси равен 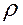. В некоторый момент к колесу прикладывают пару сил с моментом M. Определить закон движения колеса при условии, что оно катится без скольжения. Найти также максимальный момент пары, при котором возможно качение без скольжения.

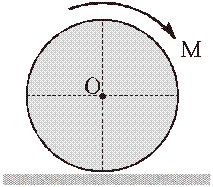
РЕШЕИЕ. Колесо будет двигаться плоскопараллельно, поэтому применим уравнения (6).

Изобразим силы, действующие на колесо при движении:

Систему координат выберем так: ось Ox – горизонтально вправо, ось Oy – вертикально вверх; начало отсчёта О – в том месте, где колесо находилось в начале движения (центр колеса С – на оси y).

Найдём

Подставив эти выражения в (6), получим

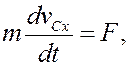
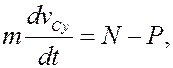
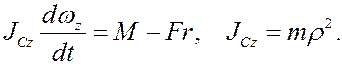
К этим уравнениям добавим уравнения связей:

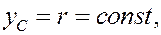
(колесо не подпрыгивает над дорогой);

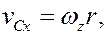
(колесо катится без скольжения, и в точке контакта колеса с дорогой – мгновенный центр скоростей).

Добавим условие качения без скольжения

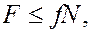
где 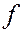– коэффициент трения скольжения, и начальные условия:

Из (10) следует

Тогда из (8) получим

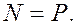
Из (11) найдём

Подставим (15) и (7) в уравнение (9)

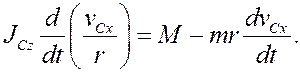
Отсюда последовательно получим

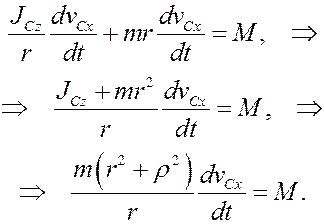
Окончательно

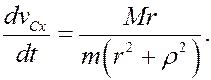
Учитывая, что правая часть (16) постоянна, при начальных условиях (13) получим

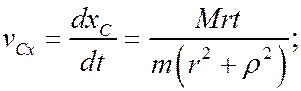
Из уравнения (7) и неравенства (12) следует

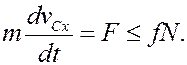
Учитывая (14) и (16), отсюда получим

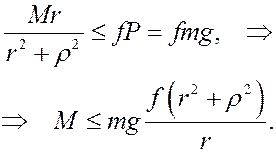
3. Дифференциальные уравнения сферического движения тела (динамические уравнения Эйлера)

Рассмотрим движение тела с одной неподвижной точкой под действием приложенных к нему сил.

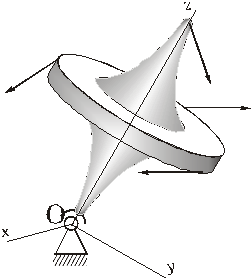
Если не требуется определения реакций шарнира О, то для решения первой, или второй, задач динамики достаточно применить теорему (3).

Для того, чтобы получить дифференциальные уравнения, при выборе координатных осей сделаем следующие предположения:

Ø выберем подвижные оси Oxyz, движущиеся вместе с телом;

Ø в качестве таких осей возьмём главные оси инерции тела для неподвижной точки (главные оси инерции – это оси для которых центробежные моменты инерции равны нулю: , ).

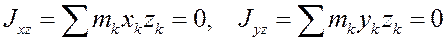В выбранных таким образом осях вектор кинетического момента тела имеет вид

Т.к. оси координат – подвижные, то для вычисления абсолютной производной применим формулу Бура

Проектируя на оси Oxyz, получим

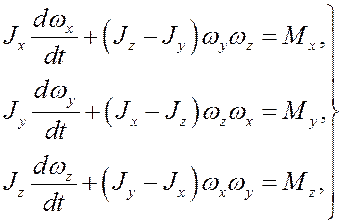
Полученные уравнения и есть дифференциальные уравнения сферического движения тела.

Эти уравнения впервые (при сделанных предположениях относительно осей координат) были получены Эйлером. Поэтому их называют динамическими уравнениями Эйлера.

Если к этим уравнениям добавить кинематические уравнения Эйлера:

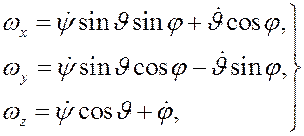
где 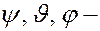углы Эйлера, то с помощью этих шести уравнений можно (в принципе!) решить как первую, так и вторую задачи динамики.

Но доказано, что для произвольного тела при произвольных силах и начальных условиях вторая задача динамики аналитически не может быть решена. При некоторых специальных предположениях о действующих силах и форме тела для произвольных начальных условий задача решена в трёх случаях: случаи Эйлера, Лагранжа и Ковалевской.

4. Определение динамических реакций опор вращающегося тела.

4.1 Понятие статических и динамических реакций связей

Если на тело наложены какие-либо связи, и тело находится в состоянии равновесия (покоя), то для определения неизвестных реакций связей можно составить условия равновесия

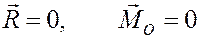
и из этих условий найти реакции.

Найденные таким способом реакции будем называть статическими реакциями и обозначать

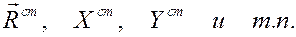
При произвольном движении тела под действием приложенных сил и в соответствии с наложенными связями реакции связей могут отличаться от статических. Поясним это простым примером.

Пусть тело может двигаться по цилиндрической поверхности радиуса R с горизонтальной образующей. Рассмотрим положение тела в наивысшей точке этой поверхности. Пусть тело находится в этом положении в покое.

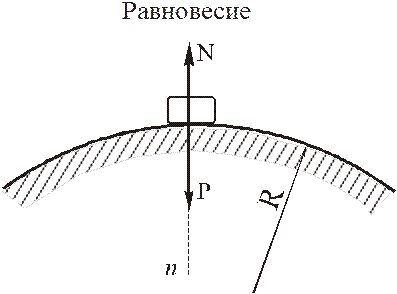
Тогда, в силу первой аксиомы статики (равновесие под действием двух сил), получим

Пусть теперь тело движется произвольным образом по этой же поверхности и в данном положении имеет скорость v.

Тело не находится в положении равновесия. Запишем дифференциальное уравнение движения тела в проекции на главную нормаль к поверхности:

Отсюда

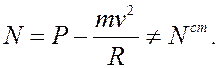
Видно, что реакция не равна статической. Если ввести обозначение

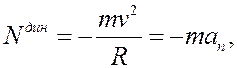
где через обозначена динамическая реакция, то реакцию связи при движении тела можно представить

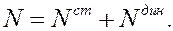
Таким образом, можем заключить.

Дата добавления: 2014-01-05