Навантаження на зубці черв'ячного колеса

Номінальні сили у зачепленні черв'ячної передачі. У навантаженій черв'ячній передачі сила взаємодії між витками черв'яка та зубцями колеса розподіляється вздовж лінії їхнього контакту. Таку розподі­лену силу замінимо зосередженою і прикладеною до зубця черв'ячно­го колеса у його середньому нормальному до осі перерізі. При цьому сили тертя у зачепленні не враховуються.

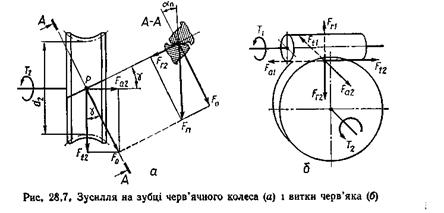
Дія обертового моменту Т₂ на валу черв'ячного колеса спричинює появу нормальної сили F_n з боку витка черв'яка на зубець колеса. Ця сила діє у площині А – А, нормальній до лінії зубця (рис. 28.7, а), напрямлена по нормалі до профілів витка та зубця у точці їх контакту і утворює кут зачеплення α_n з перпендикуляром до лінії центрів чер­в'яка і черв'ячного колеса.

Замінимо силу F_n двома її взаємно перпендикулярними складови­ми F_r2 і F_o. які перенесемо на схему черв'ячного колеса. Тут сила F_r2 проектується в точку Р, а сила F_o лежить у площині А – А і на­прямлена по дотичній до початкового циліндра колеса. Зобразимо силу F_o також у вигляді двох взаємно перпендикулярних складових F_t2 і F_а2. Отже, замість нормальної сили маємо три її взаємно перпенди­кулярні складові F_t2, F_r2 і F_a2.

Колова сила на черв'ячному колесі визначається через обертовий момент

F_t2 = 2T₂/d₂. (28.24)

Осьова сила на черв'ячному колесі подається через колову силу

F_a2 = F_t2 · tg γ. (28.25)

Для визначення радіальної сили F_r2 попередньо запишемо F₀ = F_t2 /cos γ,

а тоді дістанемо F_r2 = F₀ tg α_n = F_t2 tg α_n / cos γ.

Враховуючи, що tgα_n /cosγ = tg α, де α = 20^o – кут зачеплення у площині, перпендикулярній до осі колеса, запишемо вираз для виз­начення радіальної сили:

F_r2 = F_t2 · tg α (28.26)

Нормальна сила F_n на зубець колеса дорівнює сумі складових сил F_t2, F_r2 і F_a2, а її модуль визначається за формулою

F_n = F₀/cos α_n = F_t2 /(cos α_n · cos γ). (28.27)

На витки черв'яка з боку зубців колеса діють такі самі сили, але в протилежному напрямі (рис. 28.7, б), до того ж деякі з них міняють свою назву.

Колова сила на черв'яку дорівнює осьовій силі на черв'ячному колесі:

F_t1 = F_a2 = F_t2 · tgγ. (28.28)

Осьова сила на черв'яку дорівнює коловій силі на колегії

F_a1= F_t2 = 2T₂/d₂. (28.29)

Радіальна сила на черв'яку дорівнює радіальній силі на колесі:

F_r1=F_r2 = F_t2 · tgα. (28.30)

Розрахункове навантаження на зубці черв'ячного колеса. За розра­хункове навантаження на зубці черв'ячного колеса беремо максималь­не значення питомої сили, розподіленої по лінії контакту,

q = (F_n / l_∑) · K_β · K_v. (28.31)

де F_n – нормальна сила на зубці згідно з формулою (28.27); l_∑ – сумарна довжина контактних ліній у зачепленні. Коефіцієнт K_β, що враховує розподіл навантаження по ширині вінця черв'ячного колеса, та коефіцієнт K_v динамічного навантаження мають той самий зміст, що і в зубчастих передачах.

Наближено сумарну довжину контактних ліній у зачепленні чер­в'ячної передачі можна визначити за формулою

l_∑ = b₂ · ε_α/cosγ, (28.32)

де b₂ – ширина вінця черв'ячного колеса; γ – кут нахилу зубців, який дорівнює ділильному куту підйому витків черв'яка; ε_α – тор­цевий коефіцієнт перекриття, який у середній площині черв'ячного колеса становить 1,8–2,2.

У виразі (28.32) не врахована зігнута форма зубців черв'ячного колеса, але вона компенсується неповнотою дотикання витків та зуб­ців по дузі обхвату черв'яка 2δ Підставляючи (28.27) і (28.32) у вираз (28.31), дістанемо

q = w_t / (ε_α cos α_n). ( 28.33)

Тут w_t – питома розрахункова колова сила, що визначається за формулою

w_t = (F_t2 / b₂)K_βK_v. (28.34)

За аналогією із зубчастими передачами вирази для розрахунково­го навантаження та питомої розрахункової колової сили записують у вигляді:

– при розрахунку активних поверхонь зубців на контактну втому

q_H = w_{H t} /(ε_α · cos α_n); w_{H t} = (F_{H t2} /b₂) · К_{H β} · К_HV; (28.35)

– при розрахунку зубців на втому при згині

q_F = w_{F t} /(ε_α · cos α_n); w_{F t} = (F_{F t2} /b₂) · К_{F β} ·К_FV (28.36)

Колові сили F_{H t2} і F_{F t2} мають вигляд:

F_{H t2} = 2T_2H /d₂; F_{F t2} = 2T_2F/d₂, (28.37)

де обертові моменти T_2H = T_2F = T₂ і будуть дорівнювати макси­мальному тривало діючому обертовому моменту відповідно до заданого режиму навантаження передачі.

Для черв'ячної передачі беруть К_Hβ = К_Fβ і К_HV = К_FV.

Коефіцієнт, що враховує розподіл навантаження по ширині вінця черв'ячного колеса,

K_β = 1+(z₂/θ)³ · (1–x). (28–38)

Тут z₂ – число зубців черв'ячного колеса; θ – коефіцієнт дефор­мації черв'яка (табл. 28.5); х – коефіцієнт, що враховує вплив режиму роботи передачі на припрацьовування зубців.

Коефіцієнт K_V динамічного навантаження зачеплення черв'ячної передачі визначають залежно від ступеня точності передачі та швид­кості ковзання за табл. 28.6.

Дата добавления: 2014-01-05