Оценка параметров уравнения парной линейной регрессии

Для оценки параметров функций, линейных по параметрам, используется метод наименьших квадратов (МНК).

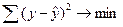МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических минимальна:

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b.

В 14 ДОБАВИТЬ ФОРМУЛЫ ВРУЧНУЮ

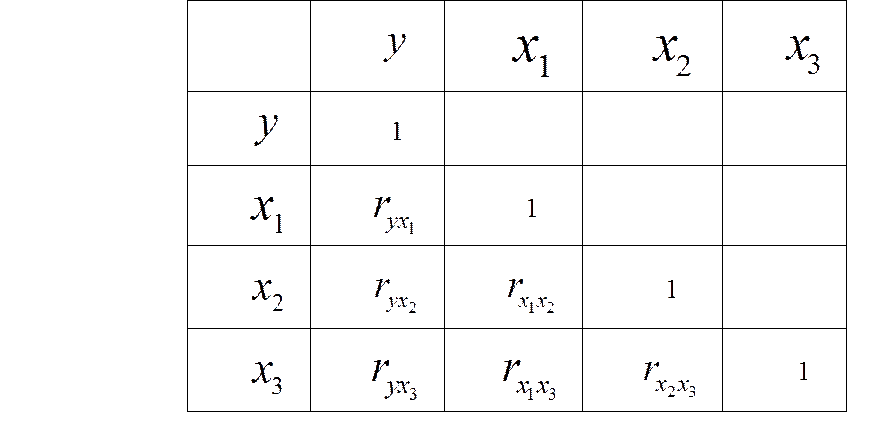17)

p Наиболее часто используются следующие функции:

18)

22) Показатели частной корреляции

Частные коэф-ты (индексы) корреляции хар-ют тесноту связи м/у р-ом и соответствующим ф-ом при устранении влияния других ф-ов, включенных в уравнение регрессии. Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового ф-ра к остаточной дисперсии, имевшей место до введения его в модель.

Частные коэффициенты корреляции измеряющие влияние на у фактора х_i при неизменном уровне др. факторов можно определить по формуле:

;

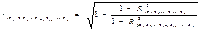- множ.коэф. детерминации всего комплекса р-ф-ов с р-ом

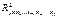- тот же показатель детерминации,но без введения в модель ф-ра х_i

Порядок частного коэф-та корреляции определяется кол-ом ф-ов, влияние которых исключается. Например, r_yx1*x2 – коэф.частной корреляции первого порядка.

При двух факторах и i=1 данная формула примет вид:

Частные коэффициенты корреляции изменяются в пределах от -1 до 1.

Дата добавления: 2014-01-05