Диференціальні рівняння теплообміну

Для отримання диференціального рівняння якого небудь явища (конвективний теплообмін). В межах цього явища виділяють нескінченно малий об’єм (наприклад пристінний шар повітря біля труби, біля скла, біля стіни). Нескінченно малий проміжок часу. Керуючись основними законами фізики складають рівняння яке описує явище в цьому нескінченно малому об’ємі. За допомогою диференціальних рівнянь не вирішують якісь кінцеві задачі – диференціальне рівняння спершу інтегрують, а потім додати до нього умови однозначності.

Є диференціальні рівняння які описують конвективний теплообмін. Основне з них диференціальне рівняння теплопровідності Фур’є-Кірхгофа. Його виводять на основі першого закону термодинаміки. 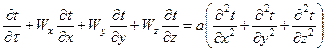. Дане рівняння зв’язує температуру з координатами простору 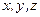та часом 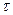- 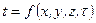. Це фактично рівняння температурного поля. В цьому рівнянні 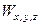- проекції руху теплоносія на координатні осі. 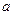- коефіцієнт температуропровідності. Позначимо для спрощення 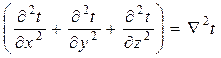(- набла означає другу похідну по координатах).

Якщо тіло тверде то для нього відсутня швидкість і рівняння набуває вигляду .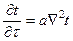

Якщо поле стаціонарне тоді ще простіше 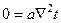- для твердого тіла стаціонарне трьохмірне температурне поле. А якщо одновимірне тоді .

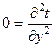Отже диференціальне рівняння Фур’є-Кірхгофа описує зміну температури в просторі і часі. Але в цьому рівнянні маємо 7 змінних величин. Його розв’язати неможливо. Тому необхідно додати інші рівняння наприклад рівняння руху теплоносія.

Можна взяти що теплоносій – рідина, крапельна нестислива. (Якщо взяти стисливе середовище то рівняння руху буде значно складніше). І для нього рівняння руху Нав’є-Стокса.

Аналогічно запишеться для осі і для осі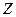

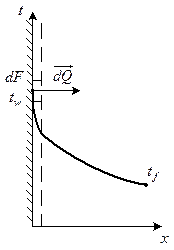
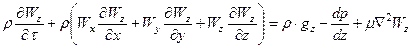. Для кожного рівняння змінною величиною виступає проекція швидкості на відповідну вісь. Отже отримали ще три рівняння. Ніби система стала замкнутою але в рівняннях руху з’явилася нова величина 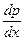і знову система не замкнена. І ця система замикається рівняння нерозривності або суцільності руху теплоносія.

. Якщо потік стаціонарний тоді 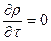. А якщо одномірний потік тоді наприклад 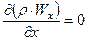. Або в інтегральному вигляді . І тепер система рівнянь замкнута і можна інтегруючи її отримати рівняння температурного поля. Але нам треба обрахувати тепловий потік. А в рівняння Ньютона-Ріхмана входить коефіцієнт тепловіддачі . То потрібно ще якесь рівняння щоб ми могли знайти тепловий потік. Це диференціальне рівняння тепловіддачі. Візьмемо якусь елементарну ділянку поверхні. Температури стінки і теплоносія. Елементарний тепловий потік. Виділяємо пристінний шар в межах якого змінюється швидкість теплоносія. Температура значно змінюється в пристінному шарі і незначно в самому теплоносії. Це характерний графік зміни температури при конвективно му теплообміні. Через цей тонкий пристінний шар з ламінарним рухом теплоносія тепловий потік передається теплопровідністю рівняння Фур’є 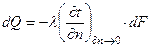. Коли тепловий потік пройшов цей шар то він передається макрометодом. Рівняння Ньютона-Ріхмана 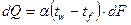. Це один і той самий тепловий потік. Якщо прирівняти праві частини отримаємо 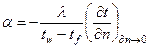- це і є диференціальне рівняння тепловіддачі.

Таким чином використовуючи систему рівнянь до якої входять наприклад рівняння теплопровідності Фур’є-Кірхгофа, рівняння руху Нав’є-Стокса і рівняння суцільності руху отримуємо рівняння температурного поля. Знаючи рівняння температурного поля знаходять градієнт температури. Потім обраховують коефіцієнт тепловіддачі після чого можна використовувати рівняння Ньютона і знаходити величину теплового потоку. Такий теоретичний шлях визначення теплового потоку.

Для отримання рівняння теплового поля систему рівнянь треба інтегрувати а для цього треба добавити умови однозначності які призвані виділити з подібних об’єктів якийсь один об’єкт.

Умови однозначності є такі:

1. Геометричні – однозначно треба сказати що ми беремо в якості об’єкта це віконне скло шириною, висотою, поверхня гладка. Коло поверхні такий об’єм повітря.

2. Фізичні – в якості теплоносія використовується повітря. В’язкість така, густина така і тд.

3. Крайові або приграничні – вимірюємо температури повітря біля поверхні, на такій відстані така, а на такій – така.

4. Часові – якщо поле стаціонарне то відповідний доданок зникає, а якщо нестаціонарне тоді треба показати як температура теплоносія змінюється з часом.

Математичний опис процесів конвективного теплообміну складається з повної системи диференціальних рівнянь (можна замість рівнянь Нав’є-Стокса прийняти і інші рівняння руху), додаються умови однозначності, додається диференціальне рівняння тепловіддачі.

Виявляється що на даний час цю систему диференціальних рівнянь ще ніхто не проінтегрував. Тому що існуючі математичні методи ще не дійшли до цього. А як же бути (як визначити коефіцієнт тепловіддачі) – доводиться цю задачу розв’язувати експериментальним шляхом.

Дата добавления: 2014-01-05