Обертального руху

Подібність кінематичних формул для поступального і

Таблиця 1

Рівномірний рух
поступальний	Обертальний
; ; .	; ; .
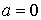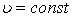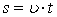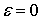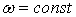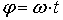Рівноприскорений рух
поступальний	Обертальний
.	.

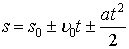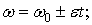
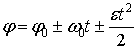Момент імпульсу матеріальної точки:

Векторний добуток радіус-вектора траєкторії матеріальної точки масою на її імпульс називається моментом імпульсу цієї точки відносно осі обертання:

.

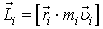Напрям вектора 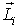(за правилом правого гвинта) показано на рис. 6.

Рис. 6

Момент імпульсу матеріальної точки (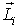) направлений перпендикулярно до площини, проведеної через 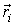і 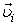і утворює з ними праву трійку векторів. (Тобто при русі від кінця вектора 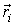до 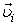правий гвинт покаже напрям вектора ).

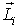У скалярній формі

.

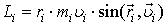Враховуючи, що при русі по колу радіус – вектор і вектор лінійної швидкості для і -тої матеріальної точки взаємно перпендикулярні:

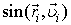=1.

Отже для обертального руху момент імпульсу матеріальної точки набере вигляду:

.

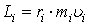Момент сили, що діє на і-ту матеріальну точку:

Векторний добуток радіус-вектора 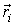, проведеного в точку прикладання сили , на цю силу називається моментом сили , що діє на і -ту матеріальну точку відносно осі обертання:

.

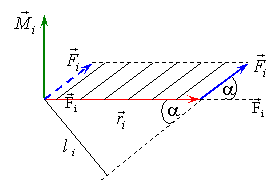
Векторне представлення моменту сили подано на рисунку 7.

В скалярній формі

.

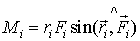Рис. 7

Вважаючи, що

,

.

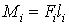Величина , що рівна довжині перпендикуляра, опущеного з точки обертання на напрям дії сили називається плечем сили .

Дата добавления: 2014-01-05