Вивід закону Кулона

Для того, щоб отримати закон Кулона з теореми Гауса, розглядають точковий електричний заряд у вакуумі. На поверхні сфери радіусом , в центрі якої розташований заряд, електричне поле повинно мати однакове значення, виходячи із міркувань симетрії. У вакуумі вектор електричної індукції 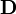дорівнює напруженості електричного поля 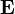(система СГС). Тому, застосовуючи теорему Гауса:

.

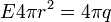Звідси основне твердження закону Кулона:

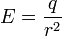
В системі СІ 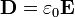, де 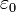- електрична стала. Теорема Гауса записується:

.

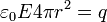Звідси:

.

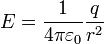Теорема Гауса в диференціальній формі

Теорему Гауса можна записати у вигляді диференціального рівняння в часткових похідних, враховуючи формулу Остроградського-Гауса (система СГС):

.

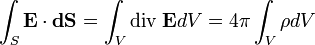Оскільки це співвідношення справедливе для будь-якого об'єму, рівними повинні бути й підінтегральні вирази:

.

В системі СІ цей вираз має вигляд:

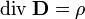
Теорема Гауса для полів у середовищі

Теорема Гауса, як одне з основних рівнянь електродинаміки, загалом, справедлива і для середовища, у своїй основній формі. Наприклад, використовуючи систему СГС:

,

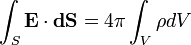якщо під Q розуміти всі заряди, враховуючи мікроскопічні. Однак, присутність зовнішнього заряду призводить до перерозподілу мікроскопічних зарядів у речовині. Тому, якщо внести зовнішній заряд q в діелектрик, то деякі із мікроскопічних зарядів, змістившись, покинуть той об'єм, по якому проводиться інтегрування, інші - увійдуть у цей об'єм зовні - речовина поляризується.

Для врахування цих ефектів в електродинаміці суцільних середовищ усі заряди розділяються на вільні та зв'язані. Вільними вважаються ті заряди, які можна привнести зовні, зяряджаючи тіла, зв'язаними - електричні заряди електронів та ядер речовини, які в зовнішніх полях зміщуються, одні відносно інших, створюючи поляризацію:

,

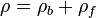де 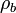- густина зв'язаних зарядів, 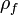- густина вільних зарядів. Густина зв'язаних зарядів пов'язана з поляризацією: .

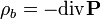Тоді теорема Гауса записується у вигляді

.

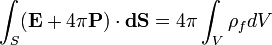Вводячи вектор електричної індукції

,

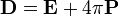отримуємо теорему Гауса для діелектричних середовищ:

,

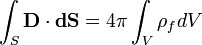або в диференціальній формі

.

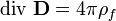Магнітне поле

Магнітні заряди (монополі) поки що експериментально не спостерігалися, тому магнітний потік через замкнену поверхню завжди дорівнює нулю:

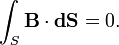
Дата добавления: 2014-01-05