Відкриті системи далекі від рівноваги

Другий закон термодинаміки, тобто закон неспадання ентропії, стверджує, що еволюція термодинамічних систем призводить до збільшення безпорядку в них. У результаті виникла ідея теплової смерті - встановлення повністю розупорядкованого рівноважного стану, коли всі перехідні процеси завершаться. Однак в природі ми часто спостерігаємо перемогу порядку над безпорадком, свідченням чого є, наприклад життя.

Закон неспадання ентропії несправедливий для відкритих термодинамічних систем у станах далеких від рівноваги. В таких системах можливий негативний притік ентропії, завдяки якому стають дозволеними процеси самоорганізації - виникнення складних впрорядкованих структур. Такі процеси вивчає синергетика.

Незважаючи на той факт, що рівняння, які задають закони руху атомів та молекул, відомі, у випадку, коли цих атомів чи молекул надзвичайно багато, марно сподіватися, що ці рівняння можна розв'язати. Проте, велике число часток в системі дозволяє застосувати статистичний підхід. Основна ідея цього підходу полягає ось у чому.

Замість того, щоб вивчати еволюцію окремої системи, розглядяють усі можливі мікроскопічні стани, в яких вона може перебувати, й проводять усереднення певних фізичних величин, підраховуючи ймовірності реалізації того чи іншого значення.

Набір усіх можливих мікоскопічних станів системи називають статистичним ансамблем.

Постулюється, що усереднення по ансамблю дає той же результат, що й усереднення по часу. Строгого доведення такого припущення не існує, але воно, схоже, дає дуже задовільні результати.

Ансамблі

Усереднення у статистичній фізиці проводиться по усіх можливих мікроскопічних станах.

Найпростішим із статистичних ансамблів є мікроканонічний ансамбль, в який включають всі мікроскопічні стани, що мають певну енергію. Мікроканонічний ансамбль використовується для опису ізольованих систем, енергія яких залишається сталою завдяки закону збереження енергії.

У випадку систем, які перебувають в тепловому контакті із середовищем (термостатом), енергія системи може змінюватися. Сталою у рівноважному стані залишається інша макроскопічна величина — температура. Такими є, зокрема, окремі області ізольованої системи. Такі системи описуються ширшим ансамблем — який називаютьканонічним.

Нарешті, якщо система може обмінюватися з середовищем не лише енергією, а й частинками, то розглядають великий канонічний ансамбль.

Розподіли

Метою статистичної фізики визначити ймовірность реалізації того чи іншого макроскопічного стану й знайти значення макроскопічних параметрів, таких як об'єм, тиск,температура, густина, тощо. Для проведення усереднення по ансамблю необхідно знати ймовірність реалізації того чи іншого мікроскопічного стану. Ця ймовірність задається функцією розподілу.

Якщо, наприклад, у класичній фізиці система описується набором координат і імпульсів частинок 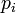, а макроскопічна величина A є функцією цих координат і імпульсів, то

,

де є функцією розподілу, а інтегрування проводиться по всьому фазовому простору.

Свої функції розподілу визначаються для кожного типу ансамблів.

Крім функцій розподілу для системи в цілому, яка визначає ймовірність реалізації певного мікроскопічного стану, часто розглядаються також одночастинкові функції розподілу, які визначають ймовірність того, що конкретна часка, атом чи молекула, перебуватиме в певному стані, наприклад, матиме певну швидкість.

Одночастинкова функція розподілу визначається через усереднення функції розподілу системи по всіх змінних, окрім певної вибраної.

.

Для однорідної в просторі системи одночастинкова функція розподілу не залежить від координати частинки, а лише від її імпульсу.

Аналогічним чином вводиться двочастинкова функція розподілу

.

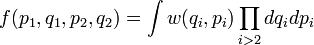Цю процедуру можна продовжити, вводячи три-, чотири- і т. д. частинкові функції розподілу.

Кореляційні функції визначають ймовірність того, що, наприклад, два атоми перебуватимуть на певній віддалі. Розглядаються двочастинкові, тричастинкові і т. д. кореляційні функції.

Класична і квантова статистична механіка

В залежності від властивостей систем, які вивчаються методами статистичної механіки, її розділяють на класичну й квантову. В класичній статистичній механіці розгляються ситеми класичних частинок, рух яких описується рівняннями Ньютона. Класична статистична фізика дає задовільні результати при високих температурах, однак при низьких температурах важливим стає квантовий характер руху частинок, що призводить до інших результатів. Рух квантових систем описується квантовими рівняннями, наприклад, рівнянням Шредінгера або аналогічним йому рівнянням для матриці густини. Для квантових частинок зовсім нового звучання набирає принцип нерозрізнюваності частинок. Як наслідок поведінка системи бозонів принципово відмінна від поведінки системи ферміонів, і обидві відрізняються від поведінки класичних частинок.

Тема 33. Функція розподілу.

Функція розподілу (2 год.) Мета:Ввести основні функції розподілу. План 1. Розподіли Фермі-Дірака Бозе-Ейнштейна і Максвелла-Больцмана. 2. Критерій виродження..

Література: [1], [3], [5], [7], [9], [10] – основна; [1] – додаткова.

Статистика Фермі—Дірака — особливий вид розподілу частинок за енергією, характерний для ферміонів.

Оскільки ферміони — це частинки, які не можуть перебувати в квантовомеханічному стані з одинаковими кватновими числами, ця заборона накладає обмеження на їхній розподіл за енергією. Ймовірність знайти ферміон у певному стані із енергією задається формулою

.

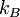Тут - хімічний потенціал, - стала Больцмана, T - температура.

Характерною особливістю цього розподілу є одиниця в знаменнику. Вона визначає особливий вигляд розподілу Фермі-Дірака.

Хімічний потенціал визначається із умови нормування розподілу й залежить від повного числа часток в системі N.

.

Властивості

В основному стані ферміони займають якомога нижчі енергетичні рівні. Накладена принципом виключення Паулізаборона призводить до того, що при нульовій тепературі, коли реалізується основний стан, усі найнижчі одноферміонні рівні зайняті. Найвищий зайнятий у такому стані рівень називається рівнем Фермі. Функція розподілу має вигляд сходинки (див. рисунок)

При збільшенні температури, існує певна ймовірність того, що ферміони системи матимуть енергію, вищу за енергію рівня Фермі. Завдяки цьому існує відмінна від нуля ймовірність того, що рівень із енергією нижчою за енергією рівня Фермі, стане вільним. Чим вища тепература, тим пологішою стає крива розподілу. При дуже високих температурах розподіл Фермі-Дірака переходить у класичний розподіл Максвела-Больцмана

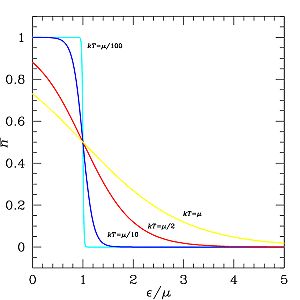
Розподіл Фермі-Дірака при різних температурах

Стати́стика Бозе—Ейнштейна — розподіл за енергією часток, які належать до бозонів.

За розподілом Бозе-Ейнштейна ймовірність того, що в квантовомеханічній багаточастинковій системі існує бозон у одночастинковому квантовому стані ^[1] із енергією визначається формулою

,

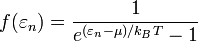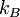де — хімічний потенціал, — стала Больцмана, T — температура.

Оскільки ймовірність повинна бути додатним числом, значення хімічного потенціалу завжди менше за енергію основного станубозонів.

Якщо кількість бозонів строго визначена (N), то хімічний потенціал визначається із умови нормування розподілу.

Фізична природа

Квантові частки бозони відрізняються від частинок класичної фізики тим, що їх принципово неможливо розрізнити (дивіться принцип нерозрізнюваності часток). Крім того,хвильова функція бозонів завжди симетрична відносно перестановок частинок. Це призводить до зміни кількості можливих станів. Наприклад, розглянемо систему, у якій можливі два одночастинкові стани 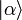і . Для двох таких частинок у класичній фізиці існує 4 можливі стани:

, , ,

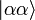У квантовій фізиці можливі лише три стани:

, ,

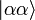Таким чином, у найпростішому випадку, за однакової енергії станів, ймовірність реалізації конкретного стану у класичній фізиці дорівнює 1/4, а у квантовій фізиці — 1/3.

При розгляді великого числа частинок і одночастинкових станів для цих частинок, для ймовірності заповнення стану отримують наведену вище формулу розподілу Бозе-Ейнштейна. Доведення можна знайти у підручниках із статистичної фізики, наведених у джерелах.

Наслідки

Одним із наслідків квантової статистики Бозе-Ейнштейна є можливість існування у тривимірних системах за низьких теператур особливої фази речовини, що складається з бозонів — Бозе-конденсату.

Статистиці Бозе-Ейнштейна підкоряється електромагнітне випромінювання, яке перебуває у тепловій рівновазі з тілом. Тому її застосування пояснює спектр випромінювання абсолютно чорного тіла.

Застосування статистики Бозе-Ейнштейна дозволило пояснити температурну залежність теплоємності твердого тіла за низьких температур (див. температура Дебая, закон Дебая).

Статистика Максвелла — Больцмана — статистичний метод опису фізичних систем, що містять велику кількість невзаємодіючих частинок, що рухаються за законами класичної механіки (тобто класичного ідеального газу); запропонована в 1871 р. австрійським фізиком Л. Больцманом.

Вивід розподілу

Із загального розподілу Ґіббса. Розглянемо систему частинок, що знаходиться в однорідному полі. В такому полі кожна молекула ідеального газу має повну енергією

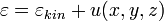, де

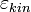— кінетична енергія її поступального руху, а — потенційна енергія в зовнішньому полі, яка залежить від її положення.

Підставимо цей вираз для енергії у розподіл Ґіббса для молекули ідеального газу 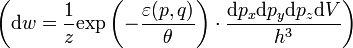(де 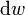— ймовірність того, що частка перебуває в стані зі значеннями координат і імпульсів 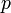, в інтервалі )

маємо:

,

де статистичний інтеграл рівний:

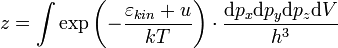
інтегрування ведеться по всіх можливих значень змінних. Далі статистичний інтеграл можна написати у вигляді:

,

ми знаходимо, що нормоване на одиницю розподіл Ґіббса для молекули газу при наявності зовнішнього поля має вигляд:

.

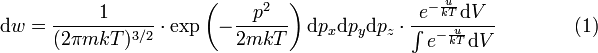Отриманий розподіл ймовірностей, що характеризує ймовірність того, що молекула має даний імпульс і знаходиться в даному елементі об'єму, носить назву розподіл Максвелла - Больцмана.

Деякі властивості

При розгляді розподілу Максвелла - Больцмана, кидається в очі важлива властивість - його можна представити як добуток двох множників:

.

Перший множник є не що інше, як розподіл Максвелла, воно характеризує розподіл ймовірностей по імпульсах. Другий множник залежить лише від координат частинок і визначається видом її потенційної енергії. Він характеризує ймовірність виявлення частки в обсязі dV.

Згідно з теорією ймовірностей, розподіл Максвелла - Больцмана можна розглядати як добуток ймовірностей двох незалежних подій - ймовірність даного значення імпульсу та даного положення молекули. Перша з них:

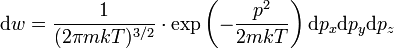
представляє розподіл Максвелла, друга ймовірність:

— розподіл Больцмана. Очевидно, що кожне з них нормовано на одиницю.

Розподіл Больцмана є окремим випадком канонічного розподілу Ґіббса для ідеального газу в зовнішньому потенціальному полі, так як за відсутності взаємодії між частками розподіл Гіббса розпадається на твір розподілів Больцмана для окремих частинок.

Незалежність ймовірностей дає важливий результат: ймовірність даного значення імпульсу абсолютно не залежить від положення молекули і, навпаки, ймовірність положення молекули не залежить від її імпульсу. Це означає що розподіл часток по імпульсах (швидкостям) не залежить від поля, іншими словами залишається тим же самим від точки до точки простору, в якому укладений газ. Змінюється лише вірогідність виявлення частки або, що те ж саме, число частинок.

Дата добавления: 2014-01-05