Основи реляційної алгебри

Реляційна модель баз даних надає можливість маніпулювати над доменами відношень. Для цих цілей існує два види апаратів маніпулювання відношеннями: реляційна алгебра (алгебра відношень) і реляційне обчислення (обчислення відношень).

Алгеброю відношень називають систему операцій маніпулювання відношеннями, кожний оператор якого в якості операнда (операндів) використовує одне чи більше відношень і утворює нове відношення за попередньо обумовленим правилом.

Реляційне обчислення дозволяє шляхом використання обчислення предикатів та кванторів змінних описувати відношення та операції над ними в вигляді аналітичного виразу або формули.

У реляційній алгебрі використовують п’ять основних операцій: об’єднання, різниця, декартовий добуток, проекція і селекція.

Проекція. Суть цієї операції полягає в тому, що береться відношення R, видаляються деякі з його компонентів і перевпорядковуються компоненти, що залишились. Якщо в результаті проекції з’являються однакові кортежі, то вони з результуючого відношення вилучаються. Операція проекції полягає в видаленні необхідних стовпців (доменів) з відношення. Нехай дано відношення СТУДЕНТ-УСПІШНІСТЬ (табл.9.1).

Таблиця 9.1

Студент-успішність

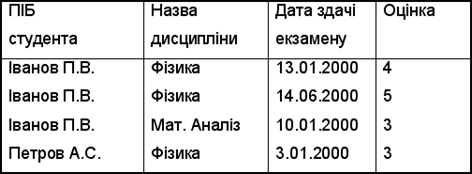
В результаті виконання операції проекції отримуємо нове відношення, яке подано в табл. 9.2.

Таблиця 9.2

Приклад операції "проекція"

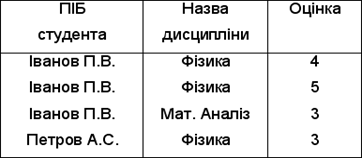
Об’єднання. Об’єднання відношень R і S (позначаться R U S) представляє собою множину кортежів, які належать R чи S або їм обом. Оператор об’єднання застосовується тільки до відношень однакової арності. Якщо в результаті об’єднання відношень мають місце однакові кортежі, то вони заміняються одним.

Нехай задано два відношення, подані таблицями 9.3, 9.4. Виконаємо над ними операцію об’єднання.

Таблиця 9.3

Викладачі-дисципліни

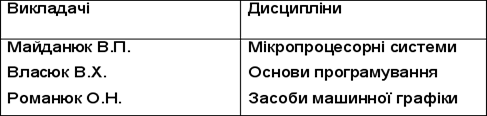
Таблиця 9.4

Викладачі-дисципліни

В результаті об’єднання відношень отримуємо результуюче відношення, яке подано в табл.9.5.

Таблиця 9.5

Викладачі-дисципліни

Різниця. Різницею відношення R і S (позначається як R - S), називається множина кортежів, які належать R, але не належать S (рис.9.1). При реалізації різниці необхідно, щоб R і S мали одну і ту ж саму арність.

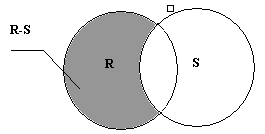
Рис. 9.1. - Графічна ілюстрація операції різниці відношень

Якщо А - відношення про жителів мікрорайону, В - відношення про тих, хто пройшов медичний огляд, то відношення А - В буде містити дані про тих жителів мікрорайону, хто не пройшов медичний огляд.

Декартовий добуток. Нехай R і S - відношення арності k₁ і k₂ відповідно. Тоді декартовим добутком відношень R і S називається множина кортежів довжини (k₁ + k₂), перші k₁ компонентів яких утворюють кортежі, які належать R, а останні k₂ - кортежі, що належать S.

Наприклад:

Таблиця 9.6

Декартовий добуток відношень СТУДЕНТИ

Результатом декартового добутку відношень СТУДЕНТИ (Табл. 9.6) та ЕКЗАМЕНИ (Табл. 9.7) буде відношення ЕКЗАМЕНАЦІЙНА ВІДОМІСТЬ (Табл. 9.8).

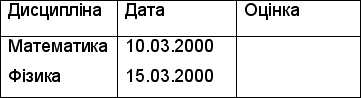
Таблиця 9.7

ЕКЗАМЕНИ

Таблиця 9.6 - СТУДЕНТИ

Таблиця 9.8

ЕКЗАМЕНАЦІЙНА ВІДОМІСТЬ

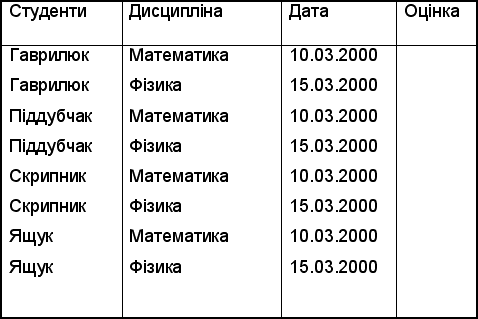
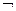Селекція. Нехай F - формула, яка може бути утворена такими засобами: а) операндами, які є константами чи номерами компонентів; б) арифметичними операторами порівняння <, =, >, ; в) логічними операторами & (І), (АБО), (НІ).

В цьому випадку E_f (R) є множина кортежів t, які належать R, таких, що при підстановці i -го компонента t замість будь-якого входження номера i в формулу F для всіх i вона стане істиною. Наприклад, E_{2 > 3} (R) означає множину кортежів, що належать R, другий компонент яких більше третього компонента.

Таблиця 9.9

Відношення

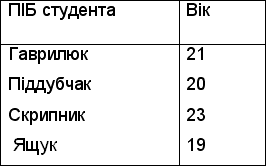
При реалізації селекції відношення, приведеного в табл.9.9, згідно з ознакою (вік > 20), отримуємо відношення (табл.9.10):

Таблиця 9.10

Відношення, над яким виконано операцію селекції

Крім перерахованих операцій існують і інші, але їх можна отримати з п’яти основних.

Розглянемо неосновні операції перетину та ділення.

Перетин R 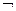S двох відношень R та S знаходиться згідно формул (R - (R - S)). Нехай R та S є відношення арності r і s відповідно, де (r > s) і S 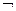{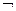}. Тоді частка R 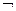S є множина кортежів t довжини (r - s) таких, що для всіх кортежів u довжини s, які належать S, кортеж tu належить R. Виконаємо операцію ділення над відношеннями, які подані відповідно таблицями 9.11 та 9.12.

Таблиця 9.11

Екзаменаційна відомість

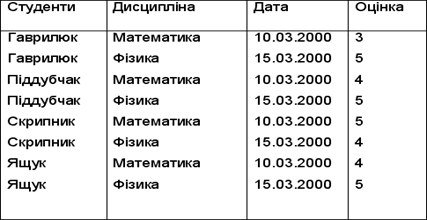
Таблиця 9.12

Дата добавления: 2014-01-05