Построение степенной модели парной регрессии

Уравнение степенной модели имеет вид: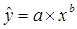

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

lg ŷ = lg a + b lg x

	Факт	Lg(Y)	Переменная	Lg(x)
	Y(t)		X(t)
	64.0	1.806		1.806
	56.0	1.748		1.833
	52.0	1.716		1.914
	48.0	1.681		1.881
	50.0	1.699		1.924
	46.0	1.663		1.982
	38.0	1.580		2.000
		11.893		13.340
Сред.знач.	50.5714	1.699	81.429	1.906

Обозначим Y = lg ŷ, X = lg x, A = lg a. Тогда уравнение примет вид:

Y = A + b X - линейное уравнение регрессии.

Рассчитаем его параметры, используя данные таблицы 3.6

Таблица 3.6

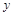
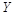
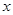
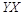
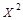
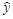
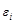
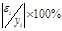
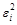
		1,8062		1,8062	3,2623	3,2623	61.294	2.706	4.23	7.322
		1,7482		1,8325	3,2036	3,3581	58.066	-2.066	3.69	4.270
		1,7160		1,9138	3,2841	3,6627	49.133	2.867	5.51	8.220
		1,6812		1,8808	3,1621	3,5375	52.580	-4.580	9.54	20.976
		1,6990		1,9243	3,2693	3,7029	48.088	1.912	3.82	3.657
		1,6628		1,9823	3,2960	3,9294	42.686	3.314	7.20	10.982
		1,5798		2,0000	3,1596	4,0000	41.159	-3.159	8.31	9.980
итог		11,8931		13,3399	22,6370	25,4528		0,51	42.32	65.407

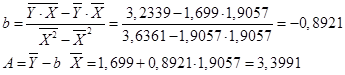
Уравнение регрессии будет иметь вид:

Y=3.3991-0,8921 X

Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.

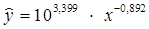
Получим уравнение степенной модели регрессии:

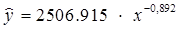
Определим индекс корреляции:

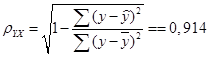
Связь между показателем y и фактором x можно считать достаточно сильной.

Коэффициент детерминации: 0.836

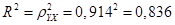
Вариация результата Y (объема выпуска продукции) на 83,6 % объясняется вариацией фактора Х (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

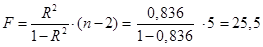
F>F_ТАБЛ = 6,61 для a = 0,05. к1=m=1, k2=n-m-1=5

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т. к. F>F_ТАБЛ.

Средняя относительная ошибка

.

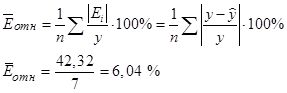В среднем расчетные значения ŷ для степенной модели отличаются от фактических значений на 6,04 %.

Дата добавления: 2014-01-05