Понятие о Z-преобразовании

Z-изображением решетчатой функции f

называется сумма ряда:

f0 + f1z-1 + f2z-2 + …+ fkz-k + …=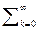fkz-k = Z { f}. (18) Иногда Z-изображение решетчатой функции f удобно обозначить символом F(z).

Основные свойства Z-изображений:

1) сумме решетчатых функций соответствует сумма их Z-изображений:

Z{f + φ} = Z{f} + Z{φ};

2) постоянный множитель можно выносить за знак Z-изображения;

3) теорема запаздывания: если 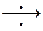f Z{ f } и функция φ запаздывает на n шагов, то φ 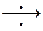z-nZ{ f },

например, при n=3:

φ={0,0,0,f0,f1,f2, …} 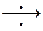Z{φ} = 0 + 0z-1+0z-2+ f0z-3 + …=

z-3 (f0 + f1z-1 + …)= z-3 Z{ f }.

В таблице 1 приведены Z-изображения решетчатых функций, полученных дискретизацией соответствующих непрерывных сигналов.

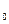Для решетчатой функции f=(f, f, ….,f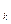,…), где f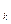=f(kτ), вводится также понятие дискретного изображения по Лапласу в виде суммы ряда:

f0 + f1e-τp + f2e-2τp + … + fke-kτp + … = 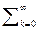fke-kτp = D { f}. (19)

Сравнивая выражение (19) с выражением для z-изображения решетчатой функции f (18), получим, что дискретное изображение по Лапласу:

D{ f} = D{f(kτ)} = F(z) | z = eτp (20).

Таким образом, дискретное изображение Лапласа решетчатой функции f получается из Z-изображения Z{ f } заменой аргумента z на eτp.

Таблица 1- Z-изображения некоторых решетчатых функций

Непрерывный сигнал f(t)	Изображение по Лапласу L{f(t)}	Дискретный сигнал	Z–изображение дискретного сигнала Z{}
1(t)		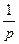1(kτ) (k=0,1, 2,…)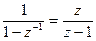
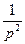
t		kτ (k=0,1, 2,…)
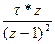
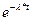
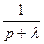
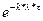		(k=0,1, 2,…)
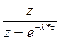
sin(ω*t)		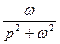Sin(k*ω*τ) (k=0,1, 2,…)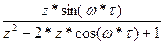
cos(ω*t)		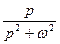cos(k*ω*τ) (k=0,1, 2,…)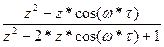

Дата добавления: 2014-01-05