Общие замечания

Удаление невидимых линий и граней

Удаление невидимых линий производится до проецирования объекта.

Алгоритмы удаления невидимых граней могут быть условно поделены на два класса в зависимости от принципов, заложенных для их реализации. Первый класс – это алгоритмы, работающие в пространстве объекта. Это означает, что для определения видимости данной грани сравнивается ее взаимное расположение со всеми остальными гранями в трехмерной сцене. Пусть N – количество граней в трехмерной сцене. Для построения трехмерной сцены в этом случае необходимо сравнить положение каждой грани с оставшимися, что требует порядка N ² операций. Например, пусть количество граней в трехмерной сцене N = 1000, тогда время работы алгоритмов этого класса порядка 1,000,000 операций.

Другой класс алгоритмов – алгоритмы, работающие в пространстве изображения, основан на нахождении точки ближайшей грани, которую пересекает луч зрения, проходящий через заданную точку на растре. Поскольку число точек на растровом экране фиксировано, то алгоритмы этого класса менее чувствительны к увеличению количества объектов в трехмерной сцене. Пусть n - число точек на растровом экране. Тогда количество операций, необходимых для построения трехмерной сцены будет порядка n ´ N. Например, для экранного разрешения 320´200 точек, n = 64000, тогда количество операций для N = 1000 граней будет порядка 64,000,000. Выбор класса алгоритма может зависеть от особенностей конкретной задачи, а также от способов реализации алгоритма.

Определение видимости или не видимости точки по сути сводится к проверке, лежат ли две точки на одном проекторе (см. рисунок …).

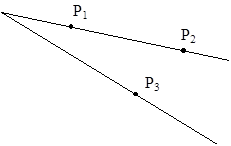
Рисунок … Проверка взаимной видимости точек

Если проекция параллельная, то проверка сводится к сравнению координат

x ₁ = x ₂, y ₁ = y ₂;

Если проекция центральная, то проверки становятся значительно сложнее:

, .

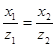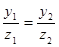Те же самые вычисления придется повторить для новой точки P₃.

Для эффективного решения задачи удаления невидимых ребер/граней преобразуем видимый объем, как показано на рис. 33.

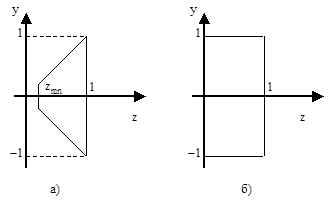
Рис. 33. Изменение видимого объема при перспективном преобразовании: а) до преобразования; б) после преобразования.

Это достигается с помощью матрицы

,

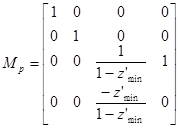которая носит название перспективного преобразования. После применения матрицы M _p нормированный видимый объем становится прямоугольным параллелепипедом, что позволяет перейти от центральной перспективной к параллельной проекции. Легко проверить, что, например,

.

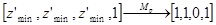При выполнении различных операций по выявлению перекрывающих друг друга граней широко используют ограничивающие грань тела (оболочки). В качестве оболочек чаще всего используют параллелепипеды с гранями, параллельными координатным плоскостям. Если такой ограничивающий грань параллелепипед задан координатами своих диагональных углов (x_min, y_min, z_min) и (x_max, y_max, z_max), то проверка пересечения оболочек двух граней сводится к простой процедуре проверки пересечения трех промежутков: от x_min до x_max, от y_min до y_max и от z_min до z_max. Если хотя бы один из этих промежутков не пересекается с аналогичным промежутком для оболочки другой грани, то оболочки граней не пересекаются и, следовательно, грани тоже не пересекаются. Грани, оболочки которых пересекаются, могут как пересекаться, так и не пересекаться, и в этом случае проводят более сложные вычисления.

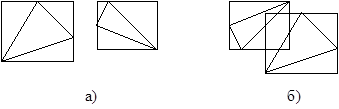
Рисунок. … Многоугольники и их оболочки: а) оболочки не пересекаются, следовательно многоугольники не пересекаются; б) оболочки пересекаются, а многоугольники нет.

Дата добавления: 2014-01-05