Метод разбиения области. Алгоритм Варнока

Алгоритм работает в пространстве изображения и анализирует область на экране дисплея (окно) на наличие в них видимых элементов. Если в окне нет изображения, то оно просто закрашивается фоном. Если же в окне имеется элемент, то проверяется, достаточно ли он прост для визуализации. Если объект сложный, то окно разбивается на более мелкие, для каждого из которых выполняется тест на отсутствие и/или простоту изображения. Рекурсивный процесс разбиения может продолжаться до тех пор, пока не будет достигнут предел разрешения экрана.

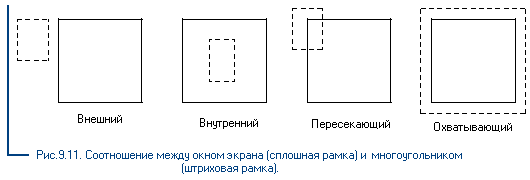
Можно выделить 4 случая взаимного расположения окна и многоугольника (рис.9.11):

§ многоугольник целиком вне окна,

§ многоугольник целиком внутри окна,

§ многоугольник пересекает окно,

§ многоугольник охватывает окно.

В четырех случаях можно сразу принять решение о правилах закраски области экрана:

· все многоугольники сцены - внешние по отношению к окну. В этом случае окно закрашивается фоном;

· имеется всего один внутренний или пересекающий многоугольник. В этом случае все окно закрашивается фоном и затем часть окна, соответствующая внутреннему или пересекающему окну закрашивается цветом многоугольника;

· имеется единственный охватывающий многоугольник. В этом случае окно закрашивается его цветом.

· имеется несколько различных многоугольников и хотя бы один из них охватывающий. Если при этом охватывающий многоугольник расположен ближе остальных к наблюдателю, то окно закрашивается его цветом.

В любых других случаях процесс разбиения окна продолжается. Легко видеть, что при растре 1024×1024 и делении стороны окна пополам требуется не более 10 разбиений. Если достигнуто максимальное разбиение, но не обнаружено ни одного из приведенных выше четырех случаев, то для точки с центром в полученном минимальном окне (размером в пиксел) вычисляются глубины оставшихся многоугольников и закраску определяет многоугольник, наиболее близкий к наблюдателю. При этом для устранения лестничного эффекта можно выполнить дополнительные разбиения и закрасить пиксел с учетом всех многоугольников, видимых в минимальном окне.

Первые три случая идентифицируются легко. Последний же случай фактически сводится к поиску охватывающего многоугольника, перекрывающего все остальные многоугольники, связанные с окном. Проверка на такой многоугольник может быть выполнена следующим образом: в угловых точках окна вычисляются Z-координаты для всех многоугольников, связанных с окном. Если все четыре такие Z-координаты охватывающего многоугольника ближе к наблюдателю, чем все остальные, то окно закрашивается цветом соответствующего охватывающего многоугольника. Если же нет, то мы имеем сложный случай и разбиение следует продолжить.

Очевидно, что после разбиения окна охватывающие и внешние многоугольники наследуются от исходного окна. Поэтому необходимо проверять лишь внутренние и пересекающие многоугольники.

Из изложенного ясно, что важной частью алгоритма является определение расположения многоугольника относительно окна.

Проверка на то что многоугольник внешний или внутренний относительно окна для случая прямоугольных окон легко реализуется использованием прямоугольной оболочки многоугольника и сравнением координат. Для внутреннего многоугольника должны одновременно выполняться условия:

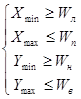
где X_min, X_max, Y_min, Y_max – ребра оболочки, W_л, W_п, W_н, W_в – ребра окна.

Для внешнего многоугольника достаточно выполнение любого из следующих условий:

Таким способом внешний многоугольник, охватывающий угол окна не будет идентифицирован как внешний (см. рис.9.12).

Проверка на пересечение окна многоугольником может быть выполнена проверкой на расположение всех вершин окна по одну сторону от прямой, на которой расположено ребро многоугольника. Пусть ребро многоугольника задано точками P ₁(x ₁, y ₁, z ₁) и P ₂(x ₂, y ₂, z ₂), а очередная вершина окна задается точкой P ₃(x ₃, y ₃, z ₃). Z – координата векторного произведения P₁P₃´ P₁P₂, равное (x ₃ – x ₁)(y ₂ – y ₁) – (y ₃ – y ₁)(x ₂ – x ₁) будет меньше 0, равно 0 или больше 0, если вершина лежит слева, на или справа от прямой P₁P₂. Если знаки различны, то окно и многоугольник пересекаются. Если же все знаки одинаковы, то окно лежит по одну сторону от ребра, т.е. многоугольник может быть либо внешним, либо охватывающим.

Вернемся к примеру 9.12. Такой многоугольник рассмотренными тестами не был идентифицирован ни как внутренний ни как пересекающий. Т.е. он может быть либо внешним, либо охватывающим. Для завершающей классификации может использоваться тест с подсчетом угла, рассматривавшийся ранее для определения нахождения точки внутри/вне многоугольника. В этом тесте вычисляется суммарный угол, на который повернется луч, исходящий из некоторой точки окна (обычно центра), при последовательном обходе вершин многоугольника.

Если суммарный угол равен 0, то многоугольник - внешний. Если же угол равен N×360^°, то многоугольник охватывает окно N раз. Простейшая иллюстрация этого теста приведена на рис.9.13.

Дата добавления: 2014-01-05