Седиментационная устойчивость дисперсных систем

Относительная устойчивость (ОУ) - это способность системы в течение определенного времени сохранять неизменной свою структуру, т.е. размеры частиц и их равномерное распределение в объеме системы.

ВИДЫ ОТНОСИТЕЛЬНОЙ УСТОЙЧИВОСТИ ДИСПЕРСНЫХ СИСТЕМ

ЛЕКЦИЯ №5

Электрокинетический потенциал, факторы, влияющие на величину электрокинетического потенциала

Дзета - потенциал обычно определяют опытным путем, т.к. все электрокинетические явления зависят от его величины и знака.

Величина дзета - потенциала определяется:

- величиной термодинамического потенциала (j₀) и характером падения потенциала в ДЭС (j _d);

- характером движения жидкости вблизи твердой поверхности (именно он будет определять местоположение плоскости скольжения), который зависит от реологических свойств дисперсионной среды, главным образом от вязкости среды (h).

Образование дисперсных систем сопровождается увеличением свободной энергии системы. Следовательно, дисперсная система является принципиально (термодинамически) неустойчивой системой, т.е. рано или поздно самопроизвольно она разрушится. Поэтому можно говорить только об относительной устойчивости (ОУ) дисперсных систем.

Относительная

устойчивость

Седиментационная устойчивость -способность дисперсной системы сохранять неизменным во времени распределение частиц по объему системы, т.е. это способность системы противостоять действию силы тяжести.

Агрегативная устойчивость - способность дисперсной систе-мы сохранять неизменной во времени степень дисперсности, т.е. размеры частиц и их индивидуальность.

Как видим, эти два вида ОУ различны по своим “задачам” и, надо полагать, по механизму, с помощью которого решаются эти задачи.

Чтобы оценить седиментационную устойчивость дисперсной системы мы должны знать следующие ее характеристики:

r - радиус частицы дисперсной фазы, тогда ее объем (V) будет равен 4/3 p r³;

r - плотность частицы дисперсной фазы;

r₀ - плотность дисперсионной среды;

h - вязкость дисперсионной среды.

В соответствии с законом Архимеда эффективная масса частицы (m `): m` = V (r - r₀)

Если (r - r₀) > 0, т.е. r >r₀, то частица будет оседать; если (r - r₀) < 0, т.е. r < r₀, то частица будет всплывать. Примем, что r >r₀. Тогда частица дисперсной фазы будет оседать под действием силы тяжести (F_сед), величина которой рассчитывается по формуле:

F_сед = m g = V (r - r₀) g,

где g - ускорение свободного падения.

При оседании частицы в дисперсионной среде с вязкостью h возникает встречная сила вязкого сопротивления среды (F_тр):

F_тр = В U_сед,

где U_сед - скорость оседания частицы; В - коэффициент трения.

F_тр

F_сед

Причем, чем больше скорость седиментации (U), тем больше сила трения, замедляющая это оседание. В результате устанавливается стационарный режим седиментации, которому соответствуетF_сед = F_тр, а U_сед = const, следовательно, V (r - r₀) g = B U_сед, отсюда U_сед = V (r - r₀) g / B

Для характеристики седиментации часто используют не скорость седиментации (U_сед,), а удельный поток седиментации (i_сед).

Удельный поток седиментации (i_сед) - это число частиц, оседающих в единицу времени через сечение единичной площади нормальное к направлению седиментации.

[ i_сед ] = част. / cм² с

Из определения i_сед следует, что i_сед = U_сед n, где n - концентрация частиц в дисперсной системе, подставив значение U_сед получаем:

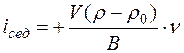
Для сферической частицы радиуса (r): V = 4/3 p r³, коэффициент трения по уравнению Стока: В = 6 ph r. Подставив эти выражения в уравнение, получаем:

i_сед = (4 p r³ (r - r₀) g n) / (3 6 ph r), проведя в нем соответствующие сокращения:

i_сед = (2 r² (r - r₀) g n) / (9h)

Таким образом, в случае сферической частицы r, поток удельной седиментации (i_сед) прямо пропорционален квадрату радиуса (r) и обратно пропорционален вязкости среды (h).

Однако, все не так просто, при рассмотрении седиментации мы не учитывали броуновского движения, которому подвержены частички микроскопических и коллоидных размеров. Следствием броуновского движения является диффузия, которая стремится выравнять концентрацию частиц по всему объему сосуда, в то время как седиментация стремится увеличить ее у дна сосуда за счет уменьшения в верхних слоях. В лекции 9 показано, что удельный поток диффузии определяется соотношением:

i_диф = - D (dn / dh), где D = kT / B

iсед iдиф

Таким образом, наблюдается два противоположных потока: поток седиментации (iсед) и поток диффузии (iдиф). К какому же результату приведет конкуренция этих двух потоков? Чтобы ответить на данный вопрос, надо рассмотреть отношение этих потоков, по сути - сравнить их величины.

Все возможные варианты можно свести к трем:

1) i_сед / i_диф >> 1; 2) i_сед / i_диф << 1; 3) i_сед / i_диф » 1.

Рассмотрим их подробнее:

1) i_сед / i_диф >> 1; i_сед >> i_диф; 4 p r³ ((r-r₀) g n)/B×3>>(-kT/B) (dn / dh)

Чтобы выполнялось это неравенство, значение Т и dn / dh должны быть невелики, а (r - r₀) и n - велики. Однако в различных системах эти параметры заметно изменить сложно, а вот радиус частицы (r) в дисперсных системах изменятеся в широком интервале: от 10^-7 до 10^-2 см и определяющими являются именно размеры частиц. Установлено, что данное соотношение наблюдается, когда радиус частицы r ³ 10^-3 см. В этом случае диффузией можно пренебречь, идет быстрая седиментация. Дисперсная система является седиментационно неустойчивой:

2) i_сед / i_диф << 1; i_сед << i_диф; 4 p r³((r-r₀) g n/B << (- kT/B) (dn / dh)

Чтобы выполнилось это неравенство значения Т и dn/dh должны быть велики, а (r - r₀) и n - невелики. Но главную роль в этом неравенстве играет значение радиуса частицы (r). Установлено, что данное соотношение наблюдается, когда радиус частицы r < 10^-5 см. В этом случае седиментацией можно пренебречь, диффузия приводит к равномерному распределению частиц по всему объему сосуда. Дисперсная система является седиментационно устойчивой.

3) i_сед / i_диф» 1; i_сед» i_диф; 4 p r³ ((r - r₀) g n/B = (- kT/B) (dn / dh)

В системе наблюдается седиментационно - диффузионное равновесие. Чтобы определить какое распределение частиц ему соответствует проинтегрируем это уравнение, предварительно разделив переменные:

4 p r³ (r - r₀) g dh = - kT (dn/n)

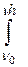- dln n = 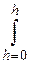((4/3 p r³ (r - r₀) g) / kT) dh

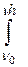- dln n = A 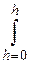dh

где n₀ - концентрация частиц на дне сосуда (h = 0);

n_h - концентрация частиц на высоте h от дна сосуда.

ln (n₀ / n_h) = Ah -ln (n₀ / n_h) = Ah n_h = n₀ exp [-Ah]

n_h = n₀ ×e^-Ah гипсометрический закон

Лотласа - Перрена

В этом случае система является седиментационно устойчивой, но распределение частиц в ней не равномерное, а равновесное. Установлено, что данное распределение наблюдается, когда радиус частиц: 10^-3 см > r > 10^-5 см.

В качестве примера рассмотрим дисперсную систему, в которой дисперсной фазой являются сферические частицы диоксида кремния (SiO₂), а дисперсионной средой - вода. Плотность частиц r₀ = 1,0 г/см³; вязкость среды h = 0,015 П. В таблице 12.1 приведены данные по седиментации в зависимости от радиуса частиц дисперсной фазы.

Таблица 12.1.

r, см	10^-3	10^-4	10^-5	10^-6	10^-7
Uсед, см/ сек	3,2 10^-2	3,2 10^-4	3,2 10^-6	3,2 10^-8	3,2 10^-10
Время, за которое частица седиментирует на 1 см	31 сек	51,7 мин	86,2 час	359 дней	100 лет

Из таблицы видно, что седиментация в лиофобных золях (r=10^-5 - 10^-7 см) протекает очень медленно. Установлено, что даже самые незначительные внешние толчки и сотрясения, а также неодинаковая температура в разных участках лиофобного золя влияют на седиментацию. Расчеты показывают, что достаточно колебаний температуры на 0,0010⁰С в 1 час, чтобы седиментация в высокодисперсном золе золота была полностью исключена.

Таким образом, седиментационная устойчивость дисперсных систем определяется, главным образом, размерами частиц дисперсной фазы:

- лиофобные золи (коллоидные растворы) (10^-7 - 10^-5 см) - седиментационно устойчивые системы, для них характерна диффузия, которая обеспечивает равномерное распределение частиц по объему системы;

- микрогетерогенные системы (10^-5 - 10^-3 см) - в них устанавливается седиментационно - диффузионное равновесие, для которого характерно гипсометрическое рапределение частиц по объему системы;

- грубодисперсные системы (> 10^-3 см) - седиментационно не-устойчивые системы, для них характерна быстрая седиментация.

Дата добавления: 2014-01-05