Учет влияния температуры и неточности изготовления элементов

Кроме внешнего силового воздействия на конструкцию может воздействовать температура (нагрев или охлаждение в ходе эксплуатации), а рабочие элементы могут иметь неточность изготовления, приводящую уже при сборке статически-неопределимой конструкции к созданию так называемых монтажных напряжений. Даже не столь существенное изменение температуры и небольшие монтажные зазоры могут существенно сказаться после нагружения конструкции внешней силой, так как при однознаковых напряжениях от всех воздействующих факторов можно получить недопустимые совокупные напряжения в рабочих элементах конструкции.

Учесть температурный и монтажный фактор можно при раскрытии статической неопределимости, включив температурный коэффициент и неточность изготовления лишних элементов в уравнения СКУМС:

,

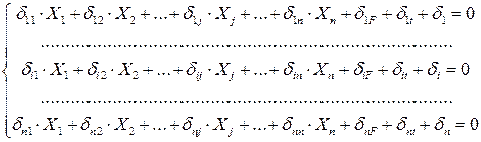где – перемещение i -той раскрепленной точки системы под действием перепада температуры 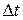. С помощью интеграла Мора его можно определить как:

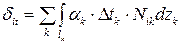(случай деформации: растяжение-сжатие),

где – коэффициент линейного расширения материала k -того рабочего элемента; 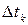– перепад температуры, испытываемый k -тым рабочим стержнем; 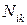– внутренняя продольная сила, возникающая на k-том рабочем элементе основной системы под воздействием единичной силы, приложенной к i -той раскрепленной точке в направлении отброшенной связи (); – неточность изготовления i -того элемента (обычно численно заданная по условию задачи).

При решении дополненной таким образом системы канонических уравнений метода сил мы получим реакции лишних связей (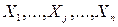), вызванные воздействием и внешних нагрузок, и температурой, и сборкой с учетом неточности изготовления рабочих элементов конструкции. Напряжения, определяемые в этом случае, также будут совокупными.

Но очень часто интересно знать вклад в совокупные напряжения каждого фактора и иметь возможность при моделировании работы конструкции варьировать величинами этих факторов. В таком случае удобнее использовать принцип суперпозиции применительно к напряжениям. Так напряжение в k -том рабочем элементе от совокупности всех факторов можно представить как:

,

а раскрытие статической неопределимости, т.е. определение реакций лишних связей, производить от каждого фактора в отдельности, решая системы:

,

,

.

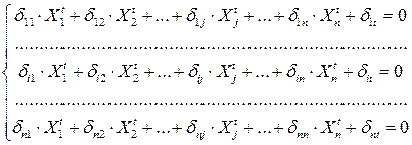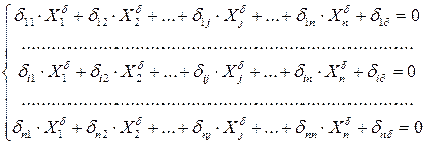Рассмотрим описанный выше прием на примере следующей задачи.

Задача.

Дана абсолютно жесткая балка ВС, закрепленная с помощью шарнирно-неподвижной опоры «О» и 2-х податливых стержней, и нагруженная двумя силами и кН (рис. 7.1). В процессе эксплуатации оба стержня нагреваются на 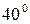С. Стержень №2 изготовлен короче необходимого размера на 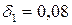% l. Площадь поперечного сечения стержней , 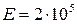МПа; коэффициент линейного расширения материала стержней 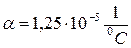, 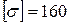МПа.

Определить напряжения, возникающие в стержнях от каждого из действующих факторов, а также суммарные напряжения. Сделать вывод о работоспособности системы в целом.

Рис. 7.1. Исходная система

Решение:

1. Образуем основную систему (рис. 7.2):

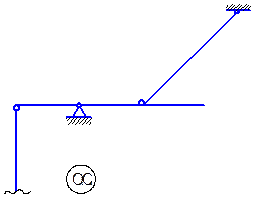
Рис. 7.2. Основная система

2. Образуем эквивалентные системы (рис. 7.3 а, рис. 7.3 б, рис. 7.3 в):

Рис. 7.3, а. Эквивалентная система с воздействием силового фактора

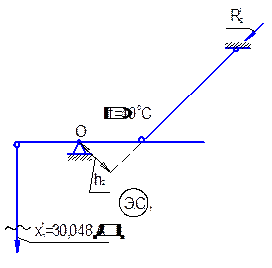
Рис. 7.3, б. Эквивалентная система с воздействием температуры

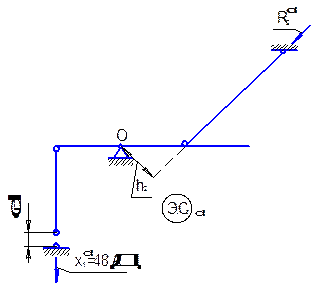
Рис. 7.3, в. Эквивалентная система с неточностью изготовления

3. Для каждой эквивалентной системы запишем условие эквивалентности:

– для (эквивалентной системы – F).

(7.2)

– для (эквивалентной системы – t).

(7.3)

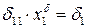– для (эквивалентной системы – ).

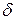(7.4)

Очевидно, что для всех 3-х эквивалентных систем коэффициент одинаков, так как все они построены на одной и той же основной системе.

4. Для определения коэффициентов 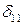, 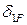поочередно нагрузим основную систему единичной силой 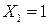(рис. 7.4) и системой внешних сил (рис. 7.5) и получим величины продольных сил в стержнях.

Рис. 7.4. Основная система, нагруженная

;

.

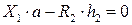
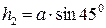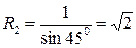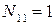; – основание: метод сечений.

.

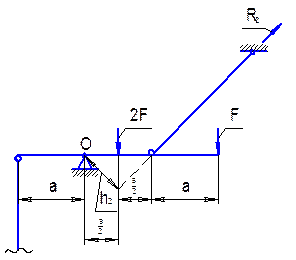
Рис. 7.5. Основная система, нагруженная внешними силами

В данном случае работает только стержень №2, в точке его крепления возникнет реакция 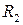, которую определим из :

;

; ;

.

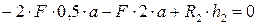
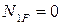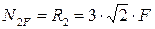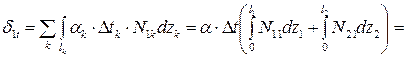
Решим каждое уравнение (7.2, 7.3, 7.4) относительно неизвестных , , .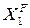

;

;

.

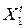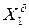Каждое значение поставим на соответствующую эквивалентную систему (рис. 7.3 а, рис. 7.3 б, рис. 7.3 в) и определим для каждой эквивалентной системы реакцию в точке крепления второго стержня, используя уравнение равновесия: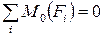

;

;

;

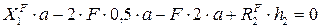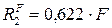
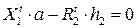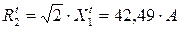
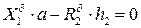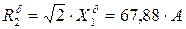
Определим напряжения в стержнях от каждого из факторов.

Продольные силы и напряжения в стержнях от силы кН.

Так как 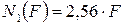, а , то

;

.

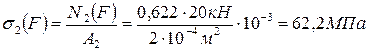Продольные силы и температурные напряжения в стержнях при их равномерном нагреве на .

;

;

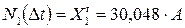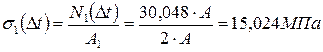(стержень растянут);

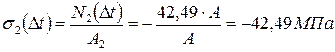(стержень сжат).

Продольные силы и сборочные напряжения в стержнях в результате неточности изготовления 1-го стержня (короче на 0,08%).

;

;

(стержень растянут);

(стержень сжат).

Суммарные продольные усилия и напряжения в стержнях от совокупности действия факторов.

;

;

;

;

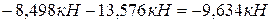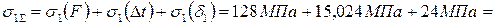
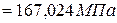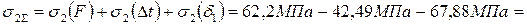
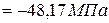Из результатов расчета видно, что в стержне №1 развиваются напряжения растяжения, превышающие допускаемую величину. Перегруз составляет 7,024 МПа, что в процентном соотношении от 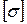составляет: 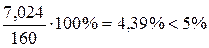, то есть меньше допускаемого процента перегруза. Во втором стержне развивается напряжение сжатия за счет температурного воздействия и неточности изготовления, которые значительно меньше допускаемого. То есть в целом конструкция работоспособна при заданных условиях нагружения.

Дата добавления: 2014-01-05