Решение плоской задачи О.К. Мора

Прямая задача Мора

Прямая задача Мора – это задача определения напряжений на произвольной площадке по известным главным напряжениям.

Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния, причем грани этого объема являются главными площадками. Секущей площадкой, параллельной главному напряжению σ ₂, выделим из этого объема треугольную призму:

Для определения напряжений на произвольной секущей площадке, рассмотрим переднюю грань призмы

Запишем уравнения равновесия для системы сил, действующей на грани призмы.

Для оси, касательной к наклонной площадке :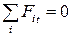

.

Сокращая общие множители и умножая все слагаемые на , получим

,

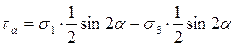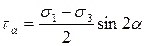. (8.2)

Для оси, нормальной к наклонной площадке :

,

откуда

.

Проведем следующие преобразования:

и получим:

. (8.3)

Возведем в квадрат каждую часть полученных выражений (8.2) и (8.3):

,

.

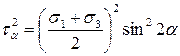Суммируя левые и правые части попарно, получим:

.

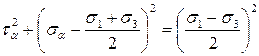Это уравнение в координатах t-s является уравнением окружности с центром в точке , и радиусом :

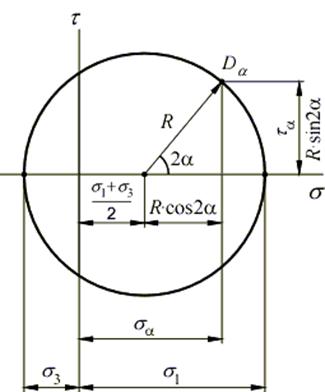
Полученная окружность называется кругом напряжений или кругом Мора. Круг Мора пересекает ось абсцисс в точках с координатами s ₁ и s ₃.

Определим координаты точки D_a:

, (8.4)

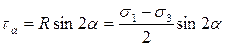, (8.5)

что совпадает с полученными ранее формулами (8.2) и (8.3).

Таким образом, каждой площадке, наклоненной под углом a к главным площадкам, на круге Мора соответствует определенная точка. Радиус этой точки составляет с осью абсцисс угол 2 a, а ее координаты определяют напряжения на площадке s_a и t_a.

Задача.

В стержне с площадью поперечного сечения A= 5х10^{-4 м2}, растягиваемом силой F = 50 кН, определить нормальное и касательное напряжения, возникающие на площадке, наклоненной под углом 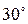к поперечному сечению стержня:

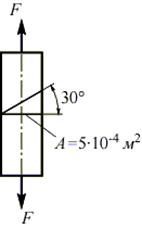
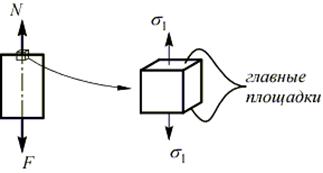
В точках поперечного сечения возникают только нормальные напряжения, то есть площадка элементарного объема в окрестностях точки, совпадающая с этим сечением, является главной:

,

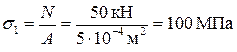остальные главные напряжения отсутствуют, т.е. это одноосное напряженное состояние.

Найдем напряжения на наклонной площадке.

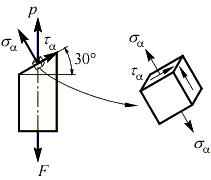
Вектор полного напряжения p, действующий на этой площадке, можно разложить на две составляющие: нормальную s_a и касательную t_a, для определения величины которых, воспользуемся кругом Мора.

Наносим в координатах t-s точки, соответствующие главным напряжениям и , и на этих точках, как на диаметре, строим круг Мора:

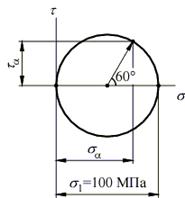
Откладывая от оси абсцисс против часовой стрелки двойной угол a, получаем на круге точку, отображающую состояние на наклонной площадке. Координаты этой точки являются искомыми напряжениями и вычисляются по формулам (8.4) и (8.5):

, .

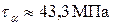Обратная задача Мора

Обратная задача Мора состоит в определении главных напряжений по известным напряжениям на произвольной площадке. Рассмотрим её на конкретном примере.

Задача.

Определить главные напряжения в опасной точке стержня, подвергающегося совместному действию изгиба и кручения:

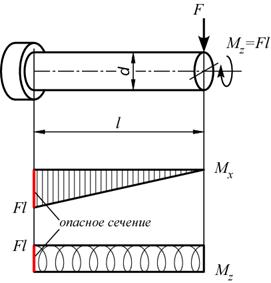
Построив эпюры внутренних силовых факторов, заключаем, что опасным сечением стержня является сечение заделки, в котором действует наибольший по величине изгибающий момент M_x.

Для нахождения опасной точки в опасном сечении рассмотрим распределение нормальных и касательных напряжений по опасному сечению:

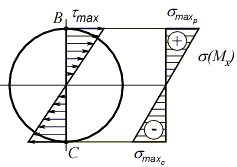
В данном случае имеется две равноопасные точки – B и C, в которых действуют максимальные нормальные и касательные напряжения, одинаковые по величине, но разные по направлению. Рассмотрим напряженное состояние в точке В, выделив в её окрестности элементарный объем и расставив вектора напряжений и на его гранях.

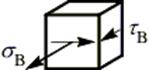
Величины напряжений и 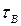можно определить по формулам:

,

.

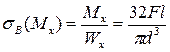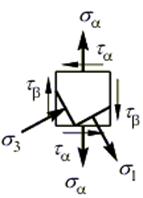
Рассмотрим выделенный куб со стороны грани, свободной от напряжений (сверху):

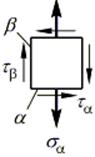
Обозначим две взаимно перпендикулярные площадки a и b. На площадке a действуют нормальное и касательное напряжение . На площадке b действуют только касательное напряжение (согласно закону парности касательных напряжений).

Порядок построения круга Мора:

1. В системе координат t-s нанести точки с координатами (s_a, t_a) и 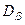(s_b, t_b). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.

2. Соединить полученные точки D_a и D_b отрезком. Точка пересечения этого отрезка с осью абсцисс O является центром круга Мора.

3. Построить окружность с центром в точке O и радиусом OD_a. Координаты точек пересечения окружности с осью абсцисс дают величины главных напряжений (в нашем случае s ₁, и s ₃).

4. Пересечение площадок a (горизонталь) и b (вертикаль) дает положение полюса площадок круга Мора P _пл (точка, в которой пересекаются все площадки).

5. Провести из полюса P _пл лучи через точки (s ₁, 0) и (s ₃, 0). Эти лучи задают положение главных площадок.

Наносим положение главных площадок и направление главных напряжений на рассматриваемую площадку:

Радиус круга Мора

,

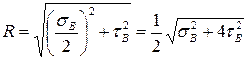тогда главные напряжения

,

.

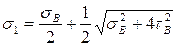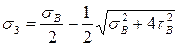Дата добавления: 2014-01-05