Метод кинематических диаграмм

Для анализа исследуемого механизма обычно необходимо знать законы перемещения, изменение скорости и ускорения ведомого звена в течение всего цикла движения, т.е. за полный оборот кривошипа. Для этого проводят графическое исследование кинематических параметров за полный цикл и по полученным значениям этих величин строят графики, которые называются кинематическими диаграммами. Кинематическая диаграмма дает наглядное графическое изображение изменения одного из кинематических параметров движения в зависимости от другого. Для перемещений S, скоростей V и касательных ускорений a ^τ точки исследуемого звена строят кинематические диаграммы в виде функций этих величин от времени t или от угла поворота φ кривошипа, т.к. при равномерном вращении последнего φ пропорционально t. Для кинематического анализа используют обычно наиболее простые ортогональные диаграммы. Особенно удобен метод кинематических диаграмм для исследования кинематики звеньев, движущихся возвратно-поступательно. В этом случае обычно строят график перемещений, откладывая расстояние движущейся точки звена от одного из крайних положений, как правило, от начала рабочего хода.

Рассмотрим построение диаграммы “пермещение-время” для ползуна кривошипно-ползунного механизма, изображенного на рис..5.

S_B=S_B(t).

Кривошип вращается равномерно, следовательно, ведущая точка A – палец кривошипа, в одинаковые промежутки времени проходит одинаковые участки пути. Строим две оси координат (рис. 6) и на оси абсцисс откладываем отрезок l в миллиметрах, изображающий в масштабе μ _t время одного полного оборота кривошипа (одного.цикла) T.

Рис..6 Диаграмма перемещений ползуна кривошипно-ползунного механизма

,
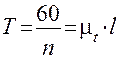где	n	–	частота вращения кривошипа, об/мин;
μ t	–	масштаб времени, с/мм
l	–	длина отрезка, изображающего время цикла, мм.

Отрезок l разбиваем на 12 равных частей и в точках 1,2,3,.….,11 откладываем параллельно оси ординат расстояния, равные перемещениям точки B от крайнего левого положения B ₀ ползуна в масштабе перемещений.μ _s. Если отрезки 1-1'= B ₀ B ₁; 2-2'= B ₀ B ₂ и т.д., то линейные масштабы плана механизма и диаграммы перемещений будут одинаковы. Соединив полученные точки 0,1',2',…..,0' плавной кривой, получаем колоколобразную кривую, которая представляет собой диаграмму перемещений, т.е. расстояний точки B (рис. 5) ползуна, измеренных от левого крайнего положения S_B=S_B(t).

При постоянной скорости вращения кривошипа ω₁ можно считать, что по оси абсцисс отложено не время t, а углы его поворота φ, т.е. диаграмма S_B=S_B(t) будет одновременно и диаграммой S_B=S_B( φ ). Масштаб угла поворота кривошипа μ_φ по оси абсцисс в этой диаграмме будет равен

.

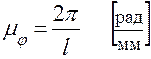Метод кинематических диаграмм основывается на правилах графического дифференцирования и интегрирования, сущность которых заключается в следующем. Построим график прямолинейного перемещения точки S=S(t) в функции времени (рис. 7).

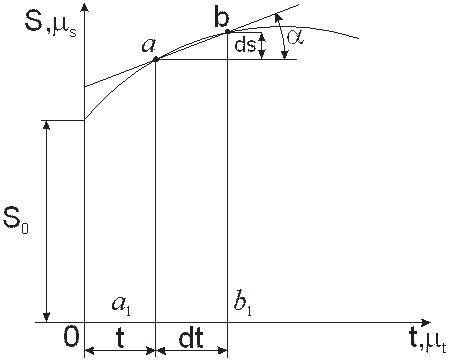
Рис. 7

По оси ординат откладываем перемещение S в масштабе 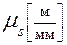, по оси абсцисс – время t в масштабе . Действительные перемещения и время определим умножением отрезков, замеренных на диаграмме на соответствующие коэффициенты. В момент времени t перемещение точки на графике определяется координатой aa₁ через бесконечно малый промежуток времени 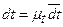перемещение точки изменится на величину 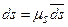и будет определяться координатой bb ₁= aa ₁+ ds; 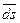и 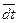– длины отрезков в мм, измеренные по соответствующим осям координат. Скорость точки 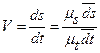. Так как 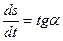, то

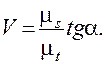(3)

То есть скорость точки пропорциональна тангенсу угла наклона касательной к графику перемещений в этой точки.

Графическое дифференцирование основано на зависимости (3). Изобразим график s=f(t) прямолинейного перемещения точки (рис..8).

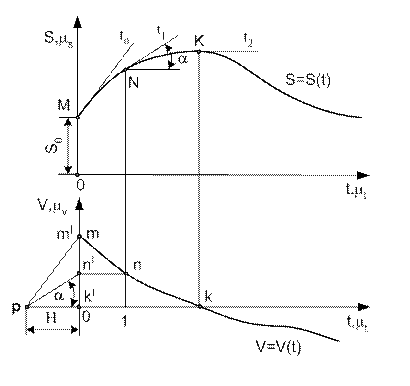
Рис. 8 Графическое дифференцирование методом касательных

Отметим на графике точки M, N, K и проведем через них касательные t ₀, t ₁, t ₂. Под графиком s=s(t) построим прямоугольную систему координат с такими же участками времени. Слева от оси перемещений отложим на оси времени на расстоянии H от начала координат точку p – полюс построения. Из полюса проведем прямые, параллельные касательным до пересечения с осью ординат pm'||t ₀; pn'||t ₁; pk'||t ₂. Полученные точки m', n', k' сносим на соответствующие ординаты и помечаем точки m, n, k, после чего соединяем их плавной кривой. Произвольная ордината полученной кривой, например on'=1n=Htg α. Таким образом, ординаты этой кривой, также как и скорость пропорциональны тангенсу наклона касательной к кривой s=s(t), следовательно они представляют собой скорость точки, движущейся прямолинейно в каком-то масштабе μ _v, который можно определить следующим образом. Истинное значение скорости

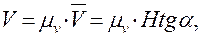(4)

где		–	ордината диаграммы скорости, мм;
μ v	–	масштаб скорости, м/с.

Приравняем правые части уравнений (3) и (4)

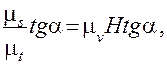
тогда масштаб скорости

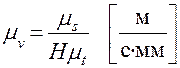(5)

Рассмотренный метод касательных на практике не совсем удобен, так как невозможно точно провести касательную к кривой без особых приспособлений. Обычно при построении кинематических диаграмм используют метод хорд, заменяя заданную кривую графиком в виде ломаной линии. Изобразим диаграмму “перемещение-время” для точки, движущейся прямолинейно (рис..9).

Рис. 9 Графическое дифференцирование методом хорд

Для этого строим две координатные оси, и ось времени разбиваем на ряд одинаковых отрезков. Точки a, b, c и т.д., обозначающие соответствующие перемещения соединяем ломаной линией. Под диаграммой s=s(t) строим прямоугольную систему координат, и ось времени разбиваем на такие же отрезки, что и на графике перемещения. От начала координат влево откладываем отрезок H и обозначим полюс p. Из полюса проводим прямые pb'||ab; pc'||bc; pd'||cd и т.д. Сносим полученные точки b', c', d' и т.д. на соответствующие ординаты и получаем ступенчатый график скорости. В середине каждого отрезка помечаем точки b ₁, c ₁, d ₁ и т.д. и соединяем их плавной кривой.

Так как 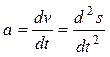, то для получения графика ускорений необходимо графически продифференцировать график скорости, пользуясь приемами, описанными выше. При криволинейном движении исследуемой точки диаграмма, построенная с использованием методов касательных или хорд будет представлять собой диаграмму тангенциальных ускорений a ^τ.

Масштаб ускорения определим по формуле

(6)

где H ₁ – полюсное расстояние диаграммы ускорений.

Подставив в выражение (6) значение μ _v из (5) получим вторую формулу для определения масштаба ускорений

.

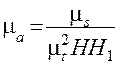Если точка движется по замкнутой траектории, то для графического дифференцирования ее перемещение рассматривается вдоль двух взаимно перпендикулярных осей.

Графическое интегрирование осуществляется как действие, обратное графическому дифференцированию.

Дата добавления: 2014-01-05