План скоростей

План скоростей строим в следующей последовательности. Вначале для механизма первого класса (0,1), затем для группы (2,3) и, наконец, для группы (4,5).

Для ведущего звена определяем скорость точки A

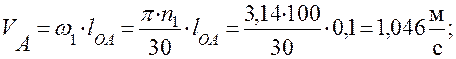
Эта скорость на плане скоростей (рис. 20) представлена вектором O_va =40 мм. Длину этого вектора удобно выбирать в пределах 70-100 мм. Определим масштаб плана скоростей

.

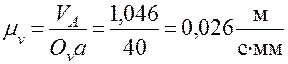Полюс плана скоростей O_v можно помещать в любой точке чертежа. Вектор O_va направлен перпендикулярно кривошипу в сторону его вращения.

Для группы Ассура (2,3) запишем два векторных уравнения для внутреннего шарнира B, соединяющего звенья 2 и 3. Рассматриваем движение центра шарнира совместно и относительно точки A, затем совместно с точкой D и относительно неё.

,
где	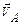–	скорость точки а, представленная вектором Ova;
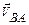–	скорость относительного вращательного движения точки B относительно точки A;
–	скорость точки D; т.к. точка D принадлежит стойке;
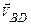–	скорость в относительном движении точки B относительно точки D.

Решаем графически записанные уравнения. Согласно первому уравнению, через точку а проводим прямую, перпендикулярную АВ, согласно второму уравнению через полюс проводим прямую перпендикулярно BD. На пересечении этих прямых отлечаем точку b, соединяем её с полюсом и получаем вектор O_vb, который изображает в масштабе абсолютную скорость точки B. Отметим, что все точки, скорость которых равна нулю, располагаются в полюсе O_v.

Скорость точки C определим используя теорему подобия. На векторе O_vb строим треугольник подобный треугольнику DBC, при этом учитываем правило обхода контура. Соединив полюс с точкой c, получим вектор абсолютной скорости точки C. Скорости центров тяжести звеньев 2 и 3 также находим при помощи теоремы подобия. На основании этой теоремы точку S₂ располагаем в середине вектора ab, а точку S₃ – в центре тяжести треугольника O_vbc. Соединив эти точки с полюсом, определяем величину и направление скоростей центров тяжести шатуна 2 и коромысла 3.

В группе (4,5) определяем скорость шарнира Е, который одновременно принадлежит и шатуну 4 и ползуну 5. Рассматривая движение точки Е совместно с точкой C и относительно неё, а затем совместно с точкой Е_x, принадлежащей направляющей х-х и совпадающей с точкой Е и относительно направляющей, запишем два векторных уравнения:

.

Вектор 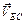перпендикулярен звену EC, т.к. представляет скорость точки E в относительном вращательном движении вокруг точки C. Т.к. направляющая неподвижна, V_x =0. Относительная скорость направлена параллельно направляющей x-x. Графически решая первое уравнение, через точку C плана скоростей проводим прямую, перпендикулярную шатуну СЕ, согласно второму уравнению проводим через полюс прямую параллельную направляющей x-x. На пересечении этих прямых отмечаем точку e, полученный вектор O_ve изображает в масштабе μ _v скорость ползуна. Для определения скорости центра тяжести шатуна 4 (точка S ₄) необходимо найти середину вектора ce и полученную точку соединить с полюсом.

Рис. 20 План скоростей механизма. μ _v = 0,026 м/с·мм

Используя построенный план, находим величины абсолютных скоростей точек.

Определим также величины относительных скоростей.

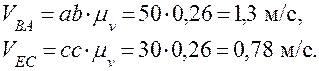
Найдем угловые скорости ω_2, ω_3, ω₄ звеньев 2,3 и 4.

Направление ω₂ определим, перенося вектор ab относительной скорости V_AB в точку B и рассматривая движение точки B вокруг точки A. Таким образом, находим, что угловая скорость звена АВ направлена по часовой стрелке.

Аналогично находим направления угловых скоростей звеньев 3 и 4. Переносим вектор O_vb скорости точки B во вращательном движении относительно точки D; угловая скорость ω₃ звена 3 также направлена по направлению движения часовой стрелки. Перенеся вектор ce относительной скорости точки Е вокруг точки C находим, что угловая скорость ω₄ звена СЕ направлена против часовой стрелки.

Дата добавления: 2014-01-05