Силы инерции в плоских механизмах

Кинетостатический силовой расчет механизмов.

Лекция 5

Задачей силового расчета является определение сил, действующих на звенья механизма и сил взаимодействия этих звеньев – то есть давлений в кинематических парах.

При силовом расчете преимущественно пользуются принципом Даламбера, известном из теоретической механике. Согласно этому принципу, если к звеньям механизма приложить активные силы и моменты пар сил, реакции связей, а также силы инерции и моменты пар сил инерции, то можно условно считать, что система сил находится в равновесии и к ней применимы уравнения статики. Этот принцип носит еще одно название – принцип кинетостатики.

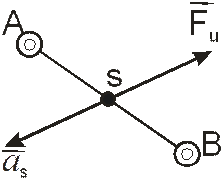
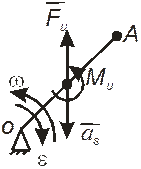
Для использования принципа кинетостатики необходимо уметь определять направления и величины сил и моментов сил инерции звеньев. В общем случае, все силы инерции звена плоского механизма, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную оси движения, приводятся к главному вектору сил инерции F_и, приложенному в центре тяжести звена S и к главному моменту пары сил инерции M_и (рис..22).

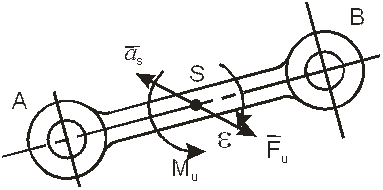
Рис. 22 Сила и момент инерции звена плоского механизма

Сила инерции F_и прикладывается к центру тяжести звена S и направлена в сторону, противоположную направлению полного ускорения точки S.

(7)

где	Fи	–	вектор сил инерции звена AB;
m	–	масса звена, кг;
as	–	вектор полного ускорения центра тяжести звена, измеряемый, м/с^2.

Из формулы (7) следует, что сила инерции имеет размерность 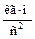, т.е. измеряется в Ньютонах. Момент пары сил инерции M_и, направлен в сторону, противоположную направлению углового ускорения звена ε _AB и рассчитывается по формуле

,
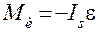где	Is	–	момент инерции звена относительно оси, проходящей через центр тяжести и перпендикулярной к плоскости движения звена, измеряемый, кг·м^2;
ε	–	угловое ускорение звена, 1/с^2.

Момент инерции I_s однородного стержня длиной l и массой m равен

.

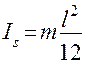Размерность момента инерци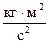и или 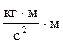, т.е. .

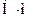Отметим частные случаи движения звеньев плоского механизма.

1. Звено движется поступательно с некоторым ускорением (рис..23а).

а	б	в

Рис. 23 Силы инерции и моменты пар инерции звеньев плоских механизмов

Так как угловое ускорение ε звена рано нулю, то момент пар сил инерции также равен нулю и все силы инерции сведутся к одной результирующей силе F_и, приложенной в центре тяжести S звена и направленной противоположно ускорению.

.

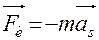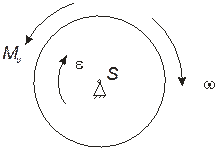
2. Звено вращается вокруг оси, проходящей через его центр тяжести S (рис..23б).

Поскольку ускорение центра тяжести равно нулю, сила инерции F_и также равна нулю. Если угловое ускорение ε звена не равна нулю, то силы инерции приводятся к паре с моментом M_и, равным

.

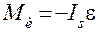При равномерном вращении (ω=const) сила инерции F_и и момент пар сил инерции M_и равны нулю.

3. Звено вращается вокруг оси O, не проходящей через центр тяжести (рис..23б).

Силы инерции сводятся к приложенной в центре тяжести S силе F_и, направленной противоположно полному ускорению a_s и к паре сил инерции с моментом M_и.

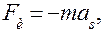(8)

,
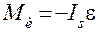где	Is	–	момент инерции звена относительно оси, проходящей через центр тяжести S.

4. Звено совершает сложное плоскопараллельное движение (рис..22).

В этом случае движение звена рассматривается как состоящее из переносного поступательного вместе с центром тяжести S и относительного вращательного вокруг центра тяжести S. Силы инерции приводятся к одной силе инерции F_и и одной паре сил M_и, которые определяются как в случае 3 в соответствии с уравнениями (8).

Дата добавления: 2014-01-05