Двигатель постоянного тока

В соответствии с принципом обратимости машина постоянного тока может работать как в качестве генератора, так и в качестве двигателя. Уравнение ЭДС для двигателя составлено на основании 2-го закона Кирхгофа с учетом направления ЭДС:

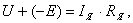
откуда

Ток в цепи якоря:

В соответствии о формулой Е_а = С_е Ф _n частота вращения определяется выражением:

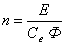
Подставим значение Е из уравнения U = Е - I_Я R_Я, получим:

т.е. частота вращения двигателя прямо пропорциональна подведенному напряжению и обратно пропорциональна магнитному потоку возбуждения.
Из этой формулы видно, что возможны пути регулирования частоты вращения двигателя постоянного тока:
1. Изменением напряжения сети U. Регулируя подаваемое напряжение Uсети можно менять частоту вращения.
2. Включением в цепь якоря добавочного сопротивлению (R'_Я = R_Я + R_ДОБ). Изменяя сопротивление R_ДОБ, меняют частоту вращения.
3. Изменением магнитного потока Ф. Машины с постоянными магнитами не регулируются. Машины с электромагнитами позволяют регулировать поток Ф путем изменения тока возбуждения I_B.
На рис. 7.5.1. показана схема включения в сеть двигателя постоянного тока.

По закону электромагнитной индукции при прохождении тока по обмотке якоря происходит взаимодействие ее проводников с магнитным полем полюсов. На каждый проводник обмотки будет действовать электромагнитная сила Р_эм = В_СРLI, пропорциональная магнитной индукции полюсов В, длине проводника L и току I, протекающему по проводнику.
Направление действия этой силы определяется правилом правой руки.
Не повторяя рассуждений, проведенных для генератора постоянного тока, запишем выражение для вращающего момента:

M=C_MФ I_Я

где C_M - коэффициент пропорциональности.
Вращающий момент у двигателей с независимым и параллельным возбуждением с увеличением нагрузки может как расти, так и уменьшаться, поскольку с ростом потребляемого тока I и размагничивания полюсов, уменьшается магнитный поток Ф.

Двигатели с последовательным возбуждением имеют отличные от вышеприведенных двигателей характеристики.
Из схемы, приведенной на рис. 7.2.1 в, видно, что магнитный поток в машине создается обмоткой возбуждения, включенной последовательно с обмоткой якоря. Следовательно, I_B = I_Я и выражение для вращающего момента будет иметь вид:

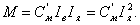
Последняя формула показывает, что чем больше нагрузка на двигатель, тем большим будет вращающий момент. Это обстоятельство делает двигатель с последовательным возбуждением незаменимым на электротранспорте (трамвае, троллейбусе и т.д.).
Реверсирование или изменение направления вращения двигателей постоянного тока может осуществляться изменением полярности тока либо в обмотке якоря, либо в обмотке возбуждения.

Дата добавления: 2014-01-05