Теорема Куна-Таккера

1. Если 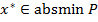– решение задачи выпуклого программирования, то найдется ненулевой вектор множителей Лагранжа , такой что для функции Лагранжа 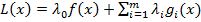выполняются условия:

а) принцип минимума для функции Лагранжа

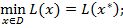
б) дополняющей нежесткости

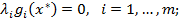
в) неотрицательности

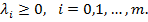
2. Если для допустимой точки 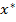выполнены условия а-в и 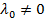, то .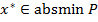

3. Если для допустимой точки 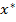выполнены условия а-в и множество допустимых элементов удовлетворяет условию Слейтера, то .

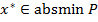Доказательство: Пусть 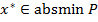. Не ограничивая общности, считаем, что 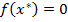. Положим

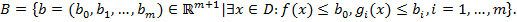
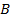– непустое выпуклое множество.

Действительно, 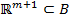, так как в определении можно положить .

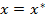Докажем выпуклость. Пусть 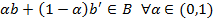. Так как 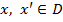, такие что

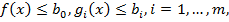
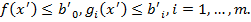
положим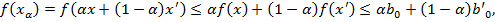

.

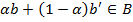Обозначим 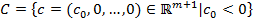– открытый луч в пространстве 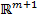. Ясно, что 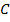– непустое выпуклое множество. Покажем, что 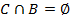. Действительно, если бы существовала точка 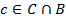, то ввиду определения множества 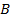отсюда следовало бы, что имеется элемент 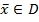, для которого выполняются неравенства 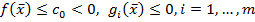. Но из этих неравенств следует, что для допустимой точки 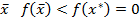, т.е. 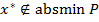. Получили противоречие с условием теоремы 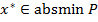. Следовательно, .

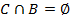По первой теореме отделимости множества 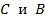можно отделить, т.е. существует вектор 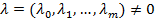, для которого

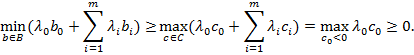
Таким образом,

(*)

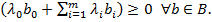1. Условие неотрицательности. Так как любой вектор с неотрицательными компонентами принадлежит 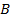, то 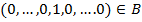, где 1 стоит на i -ом месте i= 0,… m. Подставив эту точку в (*) получим, что .

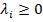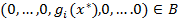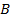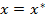Условие дополняющей нежесткости. Нетрудно видеть, что . Действительно, возьмем в определении точку , тогда 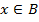и нужные неравенства выполняются. Подставив эту точку в (*), имеем 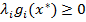. Если 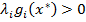, то, так как по уже доказанному условию неотрицательности 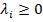, 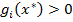– это противоречит условию допустимости точки 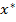. Значит, .

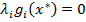Принцип максимума. Возьмем точку 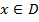, тогда точка 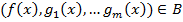. Отсюда по неравенству (*)

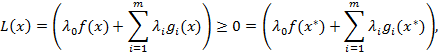
так как положили 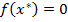и уже доказали условие дополнительной нежесткости .

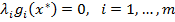2. Пусть для допустимой точки 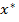выполнены условия а-в и 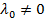. Положим 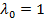. Тогда для любой допустимой точки 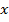будет выполняться неравенство

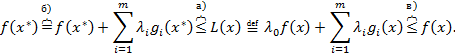
т.е. .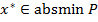

3. Пусть для допустимой точки 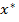выполнены условия а-в и множество допустимых значений удовлетворяет условию Слейтера. Предположим при этом, что 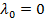. Так как 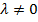, то в силу условия неотрицательности существует 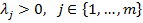. Следовательно,

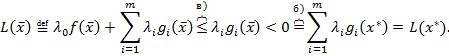
Но это неравенство противоречит условию а. Значит, наше предположение 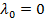не верно. Поэтому 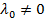, и по доказанному п. 2 .

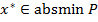Дата добавления: 2014-01-05