Симплекс-метод

Задача (P_k) называется невырожденной, если любая крайняя точка множества содержит ровно m положительных координат.

Пусть x – крайняя точка в невырожденной задаче с (для определенности) первыми m положительными координатами. Тогда вектор x можно представить в виде 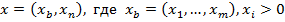– базисный вектор, 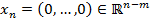– небазисный вектор.

Аналогично матрицу A можно представить в виде .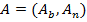

Правило решения задач по симплекс-методу

1. Привести задачу к канонической форме

2. Отыскать крайнюю точку 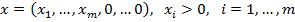, множества допустимых элементов .

3. Построить симлексную таблицу для начальной крайней точки x. Пояснения к построению таблицы:

– разложение векторов по базису 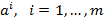. Ясно, что 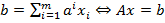. Т.е. разложением вектора 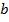является вектор 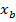ненулевых координат крайней точки .

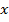Предположим, что вектора 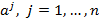имеют следующее разложение по базису . Тогда 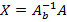, т.е. .

Очевидно, что при 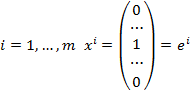. Если 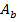– единичная матрица, то .

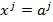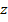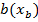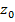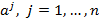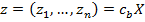В предпоследней строке в столбце под вектором запишем . Тогда – значение функционала в начальной крайней точке x. Под векторами , запишем , т.е. . Очевидно, что .

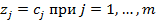В последней строке .

4. Исследовать симплексную таблицу.

а) Если , то крайняя точка x – решение задачи.

б) Если для некоторого , то значение задачи .

в) Пусть в строке 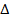имеются отрицательные числа, а соответствующие столбцы содержат положительные числа.

Предположим, что . Ясно, что 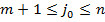. Столбец, соответствующий индексу 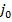называется разрешающим столбцом. Если 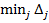достигается на нескольких значениях j, то в качестве разрешающего столбца выбираем столбец с любым таким индексом.

Обозначим . Эти значения 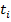ставим соответственно в последнем столбце симплексной таблицы.

Пусть 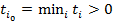. Строка вектора 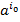называется разрешающей. Если достигается на нескольких значениях i, то в качестве разрешающей строки выбираем любую такую строку. Элемент 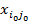называется разрешающим элементом симплексной таблицы.

Далее из числа базисных векторов исключаем вектор 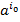, вместо него берем вектор 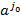. Значение функционала на новой крайней точке с новыми базисными векторами 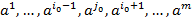возрастет на величину .

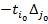5. Построить новую симплексную таблицу для нового базиса.

Способ построения новой таблицы по предыдущей (правило прямоугольника).

Ясно, что в разрешающем столбце 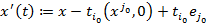. Докажем, что 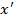является допустимым вектором. Как в п.б) выводим, что

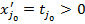
Таким образом, 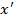является допустимым в задаче (P_k).

По построению у вектора 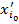. Значит, у вектора 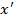является крайней точкой множества .

Заметим, что в новой симплексной таблице столбец 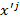строятся по указанному методу.

В старом базисе мы имели следующие разложения:

(*)

В частности, при .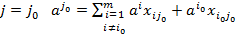

Так как 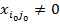, то из последнего уравнения получим

и подставим в соотношение (*). Получим разложение по базису :

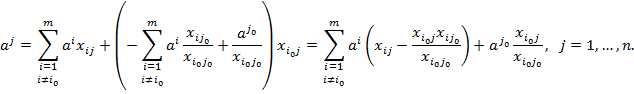
Таким образом,

Дата добавления: 2014-01-05