Преобразование координат

Координатный метод

Координатный метод был введен в XVII веке французскими математиками Р. Декартом и П. Ферма. На этом методе основывается аналитическая геометрия, которую можно считать фундаментом КГ. В современной КГ координатный метод широко используется.

Сначала рассмотрим общие вопросы преобразования координат. Пусть задана п-мерная система координат в базисе (k₁, k₂,.... k_n), которая описывает положение точки в пространстве с помощью числовых значений к_i. В КГ наиболее часто используются двумерная (n = 2) и трехмерная (n = 3) системы координат.

Если задать другую, N-мерную, систему координат в базисе (m₁, m₂,..., т) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует) можно записать в таком виде:

где f_i — функция пересчета i -й координаты, аргументами являются координаты в системе k_i,. Можно поставить и обратную задачу: по известным координатам (m₁, m₂,.... т) определить координаты (к₁, k₂,..., к_n). Решение обратной задачи запишем так:

где F_i — функции обратного преобразования.

В случае если размерности систем координат не совпадают (п ≠ N), осуществить однозначное преобразование координат чаще всего не удается. Например, по двумерным экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов.

Линейные преобразования наглядно записываются в матричной форме:

Здесь матрица коэффициентов (а_ij) умножается на матрицу-столбец (k_i), и в результате будем иметь матрицу-столбец (m_i).

Мы и дальше часто будем использовать умножение матриц, поэтому сделаем небольшой экскурс в матричную алгебру. Для двух матриц —

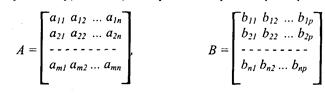
матрицы А размерами (т х п) и В — (n x p):

матричным произведением является матрица С = АВ размерами (m х р):

С = для которой элементы c_ij рассчитываются по формуле

Дата добавления: 2014-01-05