Устранение ступенчатого эффекта

Методы улучшения растровых изображений

Рассмотрим некоторые из существующих методов улучшения качества изображений, которые основываются на субъективном восприятии разрешающей способности и количества цветов. При одних и тех же значениях технических параметров устройства графического вывода можно создать иллюзию увеличения разрешающей способности или количества цветов. Причем, субъективное улучшение одной характеристики происходит за счет ухудшения другой.

В растровых системах при невысокой разрешающей способности (меньше 300 dpi) существует проблема ступенчатого эффекта (aliasing) — при большом шаге сетки растра пикселы линий образуют как бы ступени лестницы.

Рассмотрим это на примере отрезка прямой линии. Вообще говоря, растровое изображение объекта определяется алгоритмом закрашивания пикселов, соответствующих телу изображаемого объекта. Разные алгоритмы могут дать существенно отличающиеся варианты растрового изображения одного и того же объекта. Можно сформулировать условие корректного закрашивания следующим образом — если в контур изображаемого объекта попадает больше половины площади ячейки сетки растра, то соответствующий пиксел закрашивается цветом объекта (С), иначе — пиксел сохраняет цвет фона (Сф).

На рис. 3.11 показано растровое изображение толстой прямой линии, на которую для сравнения наложен идеальный контур исходной линии.

.

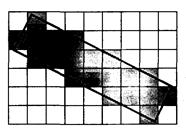
Рис. 3.11. Растровое изображение отрезка линии

Устранение ступенчатого эффекта называется на английском языке antialiasing. Для того чтобы растровое изображение линии выглядело более ровным, можно цвет угловых пикселов "ступенек лестницы" заменить определенным оттенком, промежуточным между цветом объекта и цветом фона. Будем вычислять цвет пропорционально части площади ячейки растра, покрываемой идеальным контуром объекта. Если площадь всей ячейки обозначить как S, а часть площади, покрываемой контуром, — Sx, то искомый цвет равняется

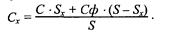
На рис. 3.12 показано сглаженное растровое изображение, построенное указанным выше методом.

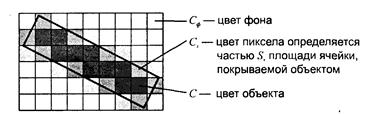
Рис. 3.12. Сглаживание

Методы визуализации сглаженных растровых изображений можно разделить на две группы. Первую группу составляют алгоритмы растеризации для отдельных примитивов — линий, фигур с заполнением. В ходе вывода последовательности примитивов для любого пиксела текущего примитива рассчитывается соответствующий цвет с учетом сглаживания.

Другую группу методов сглаживания составляют методы обработки уже существующего изображения. Для сглаживания растровых изображений часто используют алгоритмы цифровой фильтрации. Один из таких алгоритмов — локальная фильтрация. Она осуществляется путем взвешенного суммирования яркости пикселов, расположенных вокруг текущего обрабатываемого пиксела. Можно представить себе, что в ходе обработки изображения по растру скользит прямоугольное окно, которое выхватывает пикселы (рис. 3.13).

Для определения цвета текущего пиксела вычисляется некоторая функция, учитывающая значение цветов пикселов этого окна. Базовую операцию такого фильтра можно представить так:

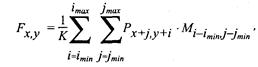
где Ρ — значение цвета текущего пиксела, F — новое значение цвета пиксела, К — нормирующий коэффициент, Μ — двумерный массив коэффициентов, который определяет свойства фильтра (обычно этот массив называют "маской").

Рис. 3.13. Окно локального цифрового фильтра

Размеры окна фильтра: 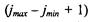— по горизонтали и (i_max – i_min +1) — по вертикали.

При 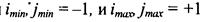имеем фильтр с окном 3x3, частоиспользуемый на практике.

Для обработки всего растра необходимо выполнить указанные выше вычисления для каждого пиксела. Если в ходе обработки новые значения цвета пикселов записываются в первоначальный растр и вовлекаются в вычисления для очередных пикселов, то такую фильтрацию называют ре курсивной. При нерекурсивной фильтрации в вычисления вовлекаются только прежние значения цвета пикселов. Нерекурсивность можно обеспечить, если новые значения записывать в отдельный массив. Рекурсивный фильтр может дать больший эффект сравнительно с нерекурсивным фильтром — изменение цвета одного пиксела может привести к изменениям пикселов всего изображения. Поведение нерекурсивного фильтра в этом смысле более предсказуемо.

На рис. 3.14 представлены результаты работы двух вариантов нерекурсивного сглаживающего фильтра, использующего окно (маску) 3х3.

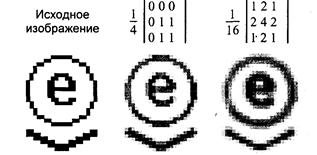
Рис. 3.14. Два сглаживающих фильтра

Значение нормирующего коэффициента здесь выбрано равным сумме элементов маски. Этим обеспечивается сохранение масштаба яркости преобразованного растра. Отметим, что маска — это не матрица, а массив коэффициентов, располагающихся соответственно пикселам окна. Средний фильтр можно задать и маской 2x2 — отбросить нулевые коэффициенты.

При сглаживании цветных изображений можно использовать модель RGB и производить фильтрацию по каждому компоненту.

С помощью локальной цифровой фильтрации можно выполнять довольно разнообразную обработку изображений — повышение резкости, выделение контуров и многое другое.

Дата добавления: 2014-01-05