Векторная полигональная модель

Для описания пространственных объектов здесь используются такие элементы: вершины, отрезки прямых (векторы), полилинии, полигоны, полигональные поверхности (рис. 7.2).

Элемент "вершина" (vertex) — главный элемент описания, все другие являются производ­ными. При использовании трехмерной декартовой системы координат вершины определяются как (x,y,z). Каждый объект однозначно определяется координатами собственных вершин.

Вершина может моделировать отдельный точечный объект, размер которого не имеет значения, а также может использоваться в качестве конечной точки для линейных объектов и полигонов. Двумя вершинами задается вектор.

Рис. 7.2. Элементы векторно-полигональной модели

Несколько векторов составляют полили­нию. Полилиния может моделировать отдельный линейный объект, толщина которого не учитывается, а также может представлять собой контур полигона.

Полигон моделирует площадный объект. Один полигон может описывать плоскую грань объемного объекта. Не­сколько граней составляют объемный объект в виде полигональной поверхности — много­гранник или незамкнутую поверхность (в литературе часто употребляется название "поли­гональная сетка").

Векторную полигональную модель можно считать наиболее распространенной в со­временных системах трехмерной КГ. Ее используют в системах автоматизированного про­ектирования, в компьютерных играх, в геоинформационных системах и т. п.

Рассмотрим структуры данных, которые используются в векторной полигональной мо­дели. В качестве примера объекта будет куб. Рассмотрим, как можно организовать описа­ние такого объекта в структурах данных.

Рис. 7.3. Первый способ описания

Первый способ. Сохраняем все грани в отдельности

Рис. 7.4. Отдельные грани

В компьютерной программе такой способ описания объекта можно реализовать разно­образно. Например, для каждой грани открывать в памяти отдельный массив. Можно все грани записывать в один массив-вектор (это уже лучше). А можно использовать классы (язык С++) как для описания отдельных граней, так и объектов в целом. Можно создавать структуры, которые объединяют тройки (x, у, z), или сохранять координаты в отдельности. Принципиально это мало что меняет — так или иначе в памяти необходимо сохранять ко­ординаты вершин граней плюс некоторую информацию в качестве накладных затрат.

Рассчитаем объем памяти, необходимый для описания куба указанным способом:

П₁ = 6 х 4 х 3 x Pв

где Pв — разрядность чисел, которые используются для пред­ставления координат вершин. Шесть граней здесь описываются 24 вершинами. Такое пред­ставление избыточно — каждая вершина записана трижды. Не учитывается то, что у граней есть общие вершины.

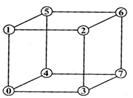
Рис. 7.5. Индексы вершин

Второй способ описания. Для этого варианта координаты восьми вершин сохраняются без повторов. Вершины пронумеро­ваны (рис. 7.5), а каждая грань представлена в виде списка ин­дексов вершин (рис. 7.6).

Рис. 7.6. Второй способ описаня

Оценим затраты памяти:

П2 = 8 x 3 x Pв +6 x 4 x Pиндекс

где Pв — разрядность координат, Pиндекс — разрядность индексов.

Третий способ. Пронумеруем также и ребра (рис. 7.7). Бу­дем сохранять грани в виде списка индексов ребер. Каждое ребро будет, в свою очередь, представлено списком индексов вершин. Этот способ в литературе иногда называют "линейно-узловой " моделью.

Оценим затраты памяти:

П₃ = 8 x 3 x Pв +12 x 2 x Pиндекс верш. +6 x4 x Риндекс ребер

где Pв - разрядность координат, Pиндекс верш. и Риндекс ребер - разрядность индексов вершин и ребер

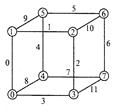
Рис. 7.7. Индексы вершин и ребер

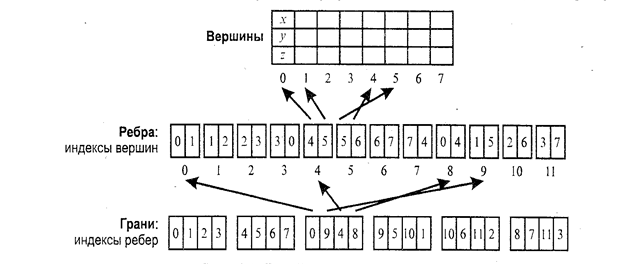
Рис. 7.8. Линейно-узловая модель

Дата добавления: 2014-01-05