Вычисление нормалей и углов отражения

Вычисление координат вектора нормали. Рассматривая модели отражения света, вы, наверное, обратили внимание на то, что нормаль к поверхности — важный элемент. Опре­деление вектора нормали к поверхности в заданной точке может быть выполнено разными способами. В значительной степени это определяется типом модели описания поверхности. Для поверхностей, заданных в аналитической форме, известны методы дифференциальной геометрии, которые основываются на вычислении частных производных функций описа­ния. Например, если поверхность задана параметрическими функциями

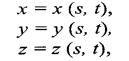
тогда координаты вектора нормали можно вычислить так:

В случае описания поверхности векторно-полигональной моделью для определения нормалей можно использовать методы векторной алгебры.

Пусть в пространстве задана некоторая многогранная поверхность. Рассмотрим одну ее плоскую грань, имеющую вид треугольника (рис. 8.4).

Для вычисления координат вектора нормали воспользуемся векторным произведением любых двух векторов, которые лежат в плоскости грани. Такими векторами могут служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного произведения были определены нами только для радиус-векторов. Чтобы перейти к радиус-векторам, вве­дем новую систему координат, центр которой совпадает с вершиной 1, а оси — параллель­ны осям бывшей системы. Координаты вершин в новой системе:

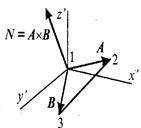
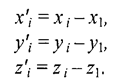
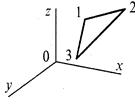
Рис. 8.4. Одна грань поверхности Радиус-векторы

Теперь назовем ребро (1-2) вектором А, а ребро (1-3) — векто­ром В, как показано на рис. 8.4. Таким образом, положение нор­мали к грани в пространстве будет описываться радиус-вектором N. Его координаты в системе (х', у', г') выразим формулами для векторного произведения

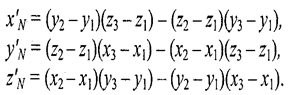
Плоская грань может быть изображена в разных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали, которое соответствует видимой стороне грани. Если плоская грань может быть видна с обратной стороны, то тогда в расчетах отраженного света необходимо выбирать для нормали обратный вектор, то есть (-N).

Если полигональная поверхность имеет не треугольные грани, а, например, плоские че­тырехугольные, то расчет нормали можно выполнять по любым трем вершинам грани.

Диффузное отражение. Рассчитаем косинус угла между вектором нормали и направле­нием на источник света. Это можно выполнить таким способом.

Сначала необходимо определить радиус-вектор, направленный на источник света. Обо­значим его как S. Потом для вычисления косинуса угла между радиус-векторами S и N вос­пользуемся формулами скалярного произведения векторов. Поскольку

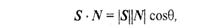
а также

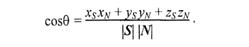то получим

Для упрощения вычислений целесообразно использовать векторы S и N единичной дли­ны, то есть |S|*|N| = 1.

Использование скалярного произведения здесь можно считать универсальным методом, который можно использовать для любого расположения точечного источника света. В от­дельных случаях можно рассчитать косинус угла падения по-иному. Например, если источ­ник света располагается на оси Z видовых координат в бесконечности позади камеры, тогда косинус угла нормали к грани с осью Z равняется отношению координаты г и длины ради­ус-вектора нормали

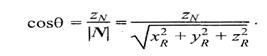
Зеркальное отражение. Будем считать, что задан радиус-вектор S, направленный на ис­точник света, а также известен радиус-вектор нормали N. Нужно найти косинус угла между отраженным лучом и направлением камеры.

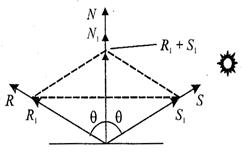Сначала необходимо вычислить радиус-вектор отраженного луча. Обозначим его как R. Выпол­ним некоторые геометрические построения, как показано на рис. 8.5.

Рис. 8.5. Векторы R1, S1 и N1 –единичной длины

Для решения нашей задачи сначала рассмот­рим единичные векторы R1, S1, и N1. Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно за­писать R1 + S1 = N¹, где N¹ — это вектор, который соответствует

диагонали ромба и совпадает по yаправлению с нормалью. Длина вектора N1 равняется 2cosq. Поскольку вектор N¹ по на­правлению совпадает с N1, то

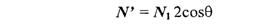или

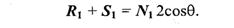
Отсюда находится единичный вектор отраженного луча:

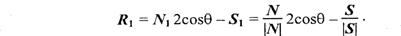
Найдем cosq. Для этого используем скалярное произведение векторов N и S:

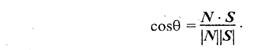
Подставим это значение в выражение для R₁:

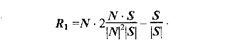
Полагая, что искомый вектор отраженного луча будет иметь такую же длину, что и вектор падающего луча, т.е. R = S R₁ , получим:

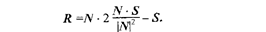
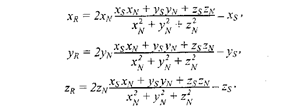Это решение в векторной форме. Запишем координаты вектора R:

Теперь осталось найти косинус угла между отраженным лучом и направлением камеры. Пусть K – радиус-вектор, направленный на камеру. Найдем искомый косинус угла:

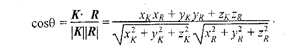
Для упрощения вычислений целесообразно задавать векторы S, N и R единичной длины (тогда и R будет единичным).

Дата добавления: 2014-01-05