Трассировка лучей

Методы трассировки лучей (Ray Tracing) на сегодняшний день считаются наиболее мо­щными и универсальными методами создания реалистичных изображений. Известно много примеров реализации алгоритмов трассировки для качественного отображения самых слож­ных трехмерных сцен. Можно отметить, что универсальность методов трассировки в значительной мере обусловлена тем, что в их основе лежат простые и ясные понятия, кото­рые отражают наш опыт восприятия окружающего мира.

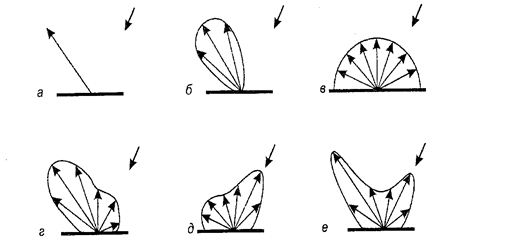
Рис. 8.12. Модели отражения: а – идеальное зеркало, б - неидеальное зеркало, в – диффузное, г – сумма диффузного и зеркального, д – обратное, е - сумма диффузного, зеркального и лбратного

Как мы видим окружающую реальность? Во-первых, нужно определиться с тем, что мы вообще способны видеть. Это изучается в специальных дисциплинах, а до некоторой степе­ни, это вопрос философский. Но здесь мы будем считать, что окружающие объекты обла­дают такими свойствами относительно света:

• излучают;

• отражают и поглощают;

• пропускают сквозь себя.

Рис. 8.13. Излучение – а – раномерно во все тороны, б - направленно

Каждое из этих свойств можно описать некоторым набором характеристик. Например, излучение можно охарактеризовать интенсивностью, направленностью, спектром. Излуче­ние может исходить от условно точечного источника (далекая звезда) или от источника рас­сеянного света (скажем, от расплавленной лавы, извергающейся из кратера вулкана). Рас­пространение излучения может осуществляться вдоль довольно узкого луча (сфокусиро­ванный луч лазера) или конусом (прожектор), или равномерно во все стороны (Солнце), или еще как-то. Свойство отражения (поглощение) можно описать характеристиками диффуз­ного рассеивания и зеркального отражения. Прозрачность можно описать ослаблением ин­тенсивности и преломлением.

Распределение световой энергии по возмож­ным направлениям световых лучей можно ото­бразить с помощью векторных диаграмм, в кото­рых длина векторов соответствует интенсивно­сти (рис. 8.12 – 8.14).

В предшествующих параграфах мы с вами уже ознакомились с видами отражения, которые упоминаются наиболее часто — зеркальным и диффузным. Реже в литературе поминается обратное зеркальное или антизеркальное от­ражение, в котором максимум интенсивности отражения соответствует направлению на источник. Обратное зеркальное отражение имеют некоторые виды растительности на по­верхности Земли, наблюдаемые с высоты рисовые поля.

Два крайних, идеализированных случая пре­ломления изображены на рис. 8.13.

Некоторые реальные объекты преломляют лучи намного более сложным образом, например, обле­деневшее стекло.

Один и тот же объект реальной действительно­сти может восприниматься как источник света, а может, при ином рассмотрении, считаться предме­том, только отражающим и пропускающим свет. Например, купол облачного неба в некоторой трехмерной сцене может моделироваться в виде протяженного (распределенного) источника света, а в других моделях это же небо выступа­ет как полупрозрачная среда, освещенная со стороны Солнца.

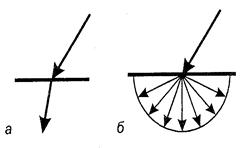
Рис. 8.14. Преломление а – идеальное, б - дифузное

В общем случае каждый объект описывается некоторым сочетанием вышеперечислен­ных трех свойств. В качестве упражнения попробуйте привести пример объекта, который обладает одновременно тремя указанными свойствами — сам излучает свет и, в то же вре­мя, отражает, а также пропускает свет от других источников. Вероятно, ваше воображение подскажет и другие примеры, нежели, скажем, раскаленное докрасна стекло.

Теперь рассмотрим то, как формируется изображение некоторой сцены, которая содер­жит несколько пространственных объектов. Будем считать, что из точек поверхности (объ­ема) излучаемых объектов выходят лучи света. Можно назвать такие лучи первичными — они освещают все другое.

Важным моментом является предположение, что световой луч в свободном пространстве распространяется вдоль прямой линии (хотя в специальных разде­лах физики изучаются также и причины возможного искривления). Но в геометрической оптике принято, что луч света распространяется прямолинейно до тех пор, пока не встре­тится отражающая поверхность или граница среды преломления. Так будем полагать и мы.

От источников излучения исходит по разным направлениям бесчисленное множество первич­ных лучей (даже луч лазера невозможно идеально сфокусировать — все равно свет будет распро­страняться не одной идеально тонкой линией, а конусом, пучком лучей). Некоторые лучи уходят в свободное пространство, а некоторые (их также бесчисленное множество) попадают на другие объекты. Если луч попадет в прозрачный объект, то, преломляясь, он идет дальше, при этом неко­торая часть световой энергии поглощается. Подобно этому, если на пути луча встречается зеркально отражающая поверхность, то он также изменяет направление, а часть световой энергии поглощается. Если объект зеркальный и одновременно прозрачный (например, обычное стекло), то будут уже два луча — в этом случае говорят, что луч расщепляется.

Можно сказать, что в результате воздействия на объекты первичных лучей возникают вторичные лучи. Бесчисленное множество вторичных лучей уходит в свободное пространство, но некоторые из них попадают на другие объекты. Так, многократно отражаясь и преломляясь, отдельные световые лучи приходят в точку наблюдения — глаз человека или оптическую систему камеры. Очевидно, что в точку наблюдения может попасть и часть первичных лучей непосредственно от источников излучения. Таким образом, изображение сцены формируется некоторым множеством световых лучей.

Цвет отдельных точек изображения определяется спектром и интенсивностью первич­ных лучей источников излучения, а также поглощением световой энергии в объектах, встретившихся на пути соответствующих лучей.

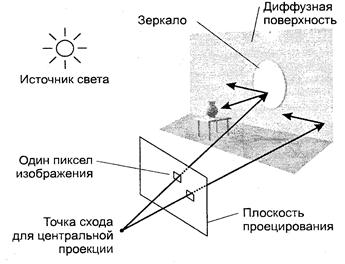
Рис. 8.15. Схема обратной трассировки лучей

Непосредственная реализация данной лучевой модели формирования изображения представляется затруднительной. Можно попробовать разработать алгоритм построения изображения указанным способом. В таком алгоритме необходимо предусмотреть перебор всех первичных лучей и определить, какие из них попадают в объекты и в камеру. Потом выполнить перебор всех вторичных лучей, и также учесть только те, которые попадают в объекты и в камеру. И так далее. Можно назвать такой метод прямой трассировкой лучей. Практическая ценность такого метода вызовет сомнение. В самом деле, как учитывать бес­конечное множество лучей, идущих во все стороны? Очевидно, что полный перебор беско­нечного числа лучей в принципе невозможен. Даже если каким-то образом свести это к ко­нечному числу операций (например, разделить всю сферу направлений на угловые секторы и оперировать уже не бесконечно тонкими линиями, а секторами), все равно остается глав­ный недостаток метода — много лишних операций, связанных с расчетом лучей, которые потом не используются. Так, во всяком случае, это представляется в настоящее время.

Метод обратной трассировки лучей позволяет значительно сократить перебор свето­вых лучей. Метод разработан в 80-х годах, основополагающими считаются работы Уитте-да и Кэя. Согласно этому методу отслеживание лучей осуществляется не от источ­ников света, а в обратном'направлении — от точки наблюдения. Так учитываются только те лучи, которые вносят вклад в формирование изображения.

Рассмотрим, как можно получить растровое изображение некоторой трехмерной сцены методом обратной трассировки. Предположим, что плоскость проецирования разбита на множество квадратиков — пикселов. Выберем центральную проекцию с центром схода на некотором расстоянии от плоскости проецирования. Проведем прямую линию из центра схода через середину квадратика (пиксела) плоскости проецирования (рис. 8.15). Это будет первичный луч обратной трассировки. Если прямая линия этого луча попадает в один или несколько объектов сцены, то выбираем ближайшую точку пересечения. Для определения цвета пиксела изображения нужно учитывать свойства объекта, а также то, какое световое излучение приходится на соответствующую точку объекта.

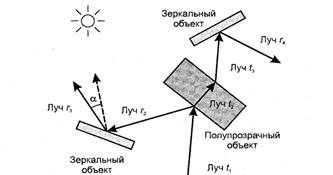
Рис. 8.16. Обратная трассировка для объектов, имеющих свойства зеркального отражения и преломления

Если объект зеркальный (хотя бы частично), то строим вторичный луч — луч падения, считая лучом отражения преды­дущий, первичный, трассируе­мый луч. Выше мы рассматри­вали зеркальное отражение и получили формулы для вектора отраженного луча по заданным векторам нормали и луча паде­ния. Но здесь нам известен век­тор отраженного луча, а как найти вектор падающего луча? Для этого можно использовать ту же формулу зеркального от­ражения, но определяя необхо­димый вектор луча падения как отраженный луч. То есть отра­жение наоборот.

Для идеального зеркала дос­таточно потом проследить лишь очередную точку пересечения вторичного луча с некоторым объектом. Что означает термин "идеальное зеркало"? Будем считать, что такое зеркало имеет идеально равную отполированную поверхность, поэтому одному отраженному лучу соответствует только один падающий луч. Зеркало может быть затемненным, то есть поглощать часть световой энергии, но все равно выполняется правило: один луч падает — один отражается. Можно рассматривать также "неидеальное зеркало". Это будет означать, что поверхность неровная. Направлению отраженного луча будут соот­ветствовать несколько падающих лучей (или наоборот, один падающий луч порождает не­сколько отраженных лучей), которые образуют некоторый конус, возможно, несимметрич­ный, с осью вдоль линии падающего луча идеального зеркала. Конус соответствует некото­рому закону распределения интенсивностей, простейший из которых описывается моделью Фонга — косинус угла, возведенный в некоторую степень. Неидеальное зеркало резко ус­ложняет трассировку — нужно проследить не один, а множество падающих лучей, учиты­вать взнос излучения от других видимых из данной точки объектов.

Если объект прозрачный, то необходимо построить новый луч, такой, который при пре­ломлении давал бы предшествующий трассируемый луч. Здесь также можно воспользо­ваться обратимостью, которая справедлива и для преломления. Для расчета вектора иско­мого луча можно применить рассмотренные выше формулы для вектора луча преломления, считая, что преломление происходит в обратном направлении (рис. 8.16).

Если объект обладает свойствами диффузного отражения и преломления, то, в общем случае, как и для неидеального зеркала, необходимо трассировать лучи, которые приходят от всех имеющихся объектов. Для диффузного отражения интенсивность отраженного све­та, как известно, пропорциональна косинусу угла между вектором луча от источника света и нормалью. Здесь источником света может выступать любой видимый из данной точки объект, способный передавать световую энергию.

Если выясняется, что текущий луч обратной трассировки не пересекает любой объект, а направляется в свободное пространство, то на этом трассировка для этого луча заканчива­ется.

Обратная трассировка лучей в том виде, в котором мы ее здесь рассмотрели, хотя и со­кращает перебор, но не позволяет избавиться от бесконечного числа анализируемых лучей. В самом деле, данный метод позволяет сразу получить для каждой точки изображения один первичный луч обратной трассировки. Однако вторичных лучей отражения уже может быть бесконечное число. Так, например, если объект может отражать свет от любого другого об­ъекта, и если эти другие объекты имеют довольно большие размеры, то какие именно точки излучающих объектов нужно учитывать для построения соответствующих лучей, например, при диффузном отражении? Очевидно, все точки.

При практической реализации метода обратной трассировки вводят ограничения. Неко­торые из них необходимы, чтобы можно было в принципе решить задачу синтеза изображе­ния, а некоторые ограничения позволяют значительно повысить быстродействие трассиров­ки. Примеры таких ограничений.

1. Среди всех типов объектов выделяются некоторые, которые назовем источниками све­та. Источники света могут только излучать свет, но не могут его отражать или прелом­лять (будем рассматривать только точечные источники света).

2. Свойства отражающих поверхностей описываются суммой двух компонентов — диф­фузного и зеркального.

3. В свою очередь, зеркальность также описывается двумя составляющими. Первая (reflection) учитывает отражение от других объектов, которые не являются источниками света. Строится только один зеркально отраженный луч r для дальнейшей трассировки. Вторая составляющая (Specular) означает световые блики от источников света. Для этого направляются лучи на все источники света и определяются углы, образованные этими лучами с зеркально отраженным лучом обратной трассировки (r). При зеркальном отра­жении цвет точки поверхности определяется цветом того, что отражается. В простейшем случае зеркало не имеет собственного цвета поверхности.

4. При диффузном отражении учитываются только лучи от источников света. Лучи от зеркально отражающих поверхностей игнорируются. Если луч, направленный на данный источник света, закрывается другим объектом, значит, данная точка объекта находится в тени. При диффузном отражении цвет освещенной точки поверхности определяется соб­ственным цветом поверхности и цветом источников света.

5. Для прозрачных (1гап5рагеп() объектов обычно не учитывается зависимость коэффици­ента преломления от длины волны. Иногда прозрачность вообще моделируют без пре­ломления, то есть направление преломленного луча I совпадает с направлением падаю­щего луча.

6. Для учета освещенности объектов светом, который рассеивается другими объектами, вводится фоновая составляющая (атbient).

7. Для завершения трассировки вводят некоторое предельное значение освещенности, ко­торое уже не должно вносить взнос в результирующий цвет, или ограничивают количе­ство итераций.

Согласно модели Уиттеда цвет некоторой точки объекта определяется суммарной интенсивностью

I(l) = KaIa(l)C(l) + KdId(l)C(l) + KsIs(l) + KrIr(l) + KtIt(l)

где λ - длина волны,

С (λ) - заданный исходный цвет точки объекта,

К_а, K_d, K_s, K_r и К_t — коэффициенты, учитывающие свойства конкретного объекта через параметры фонового подсвечивания, диффузного рассеивания, зеркальности, отражения и прозрачности,

I_a - интенсивность фонового подсвечивания,

I_d - интенсивность, учитываемая для диффузного рассеивания,

I_s - интенсивность, учитываемая для зеркальности,

I_r - интенсивность излучения, приходящего по отраженному лучу,

I_t - интенсивность излучения, приходящего по преломленному лучу.

Интенсивность фонового подсвечивания (1_а) для некоторого объекта обычно константа. Запишем формулы для других интенсивностей. Для диффузного отражения

I_d =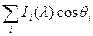

где I_i(λ) — интенсивность излучения i-ro источника света, θ_i — угол между нормалью к по­верхности объекта и направлением на i-vi источник света.

Для зеркальности:

I_d =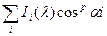

где р - показатель степени от единицы до нескольких сотен (согласно модели Фонга), α_i - угол между отраженным лучом (обратной трассировки) и направлением на г'-й источник света.

Интенсивности излучений проходящих по отраженному лучу (I_r), а так же по преломленному лучу (I_{t) ,} умножают на коэффициент, учитывающий ослабление интенсивности в зависимости от расстояния, пройденного лучом. Такой коэффициент записывается в виде е^-bd где d - пройденное расстояние, b – параметр ослабления, учитывающий свойства среды, в которой распространяется луч.

Для первичного луча необходимо задать направление, которое соответствует избранной проекции. Если проекция центральная, то первичные лучи расходятся из общей точки, для параллельной проекции первичные лучи — параллельные. Луч можно задать, например, ко­ординатами начальной и конечной точек отрезка, координатой начальной точки и направле­нием, или еще как-нибудь. Задание первичного луча однозначно определяет проекцию изображаемой сцены. При обратной трассировке лучей любые преобразования координат вообще не обязательны. Проекция получается автоматически — в том числе, не только плоская, но и, например, цилиндрическая или сферическая. Это одно из проявлений универсальности метода трассировки.

В ходе трассировки лучей необходимо определять точки пересечения прямой линии лу­ча с объектами. Способ определения точки пересечения зависит от того, кокой это объект, и каким образом он представлен в определенной графической системе. Так, например, для объектов, представленных в виде многогранников и полигональных сеток, можно использо­вать известные методы определения точки пересечения прямой и плоскости, рассмотренные в аналитической геометрии. Однако, если ставится задача определения пересечения лу­ча с гранью, то необходимо еще, чтобы найденная точка пересечения лежала внутри конту­ра грани.

Известно несколько способов проверки произвольной точки на принадлежность полиго­ну. Рассмотрим две разновидности, в сущности, одного и того же метода (рис. 8.17).

Первый способ. Находятся все точки пересечения контура горизонталью, которая соответствует координате Y заданной точки. Точки пересечения сортируются по возрастанию значений координат Х. Пары точек пересечения образуют отрезки. Если точка, которая проверяется, принадлежит одному из отрезков (для этого сравниваются координаты Х заданной точки и концов отрезков), то она – внутренняя.

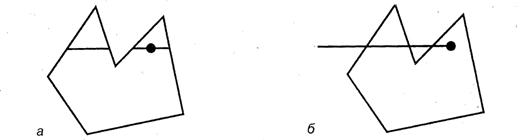
Рис. 8.17. Точка – внутренняя, если: а - точка принадлежит секущему отрезку, б – число пересечений нечетное

Второй способ. Определяется точка, лежащая на одной горизонтали с испытуемой точкой, причем требуется, чтобы она лежала вне контура полигона. Найденная внешняя точка и испытуемая являются концами горизонтального отрезка. Определяются точки пересечения данного отрезка с контуром полигона. Если количество пересечений нечетное, это значит, что испытуемая точка – внутренняя.

Если луч пересекает несколько объектов, то выбирается ближайшая точка по направлению текущего луча.

Сделаем общие выводы о относительно метода обратной трассировки лучей.

Дата добавления: 2014-01-05