Модель оценки капитальных активов

В принципе существует четкий критерий, позволяющий финансистам определить, заслуживает некоторый инвестиционный проект внимания или нет. Заслуживающие внимания инвестиционные проекты увеличивают доход акционеров фирмы.

Например, пусть котировка акций некоторой компании в настоящий момент составляет $50. На следующий год менеджерам фирмы придется принять решение об осуществлении масштабных инвестиций, и результат этого решения станет известен финансовым кругам вскоре после того, как решение будет принято. Менеджеры уверены, что если они откажутся от этой инвестиционной возможности, то компания будет в состоянии выплатить дивиденд в размере $5 на акцию, цена акции на рынке через год будет равна $53, итого стоимость акции для держателя составит $58. Если инвестиционный проект будет одобрен, то компания сможет выплатить дивиденд только в сумме $3 на акцию (так как ликвидные активы и капитализированная прибыль понадобятся для финансирования инвестиций), но цена акции в конце года составит $57, так как рынок оценит потенциальную прибыльность нового инвестиционного проекта.

В итоге получится стоимость акций $60. Не обращая внимания на дополнительные серьезные сложности, связанные с налогообложением, можно сказать, что в случае, если компания примет данный инвестиционный проект, доходы акционеров в расчете на каждую акцию будут на $2 больше, чем если она от него откажется.

На практике этот критерий не так уж легко применять. Основная трудность заключается в том, чтобы предсказать, каким именно образом инвестиции повлияют на цену акций компании.

При современном состоянии человеческого знания предложить полностью удовлетворительные методы составления подобных прогнозов невозможно. Однако мы уверены, что можно предложить такие методы, которые окажутся полезными для менеджеров.

Задачу можно разбить на две части: 1) определение основных факторов, оказывающих влияние на цену акций; 2) определение взаимосвязи между инвестиционными проектами и этими факторами. Рассмотрим теорию цен акций, известную под названием "модель оценки капитальных активов" (Capital Assets Pricing Model — САРМ). Многие основополагающие принципы этой теории интуитивно располагают к себе и известны уже давно. Некоторые факторы, влияющие на цены акций и ценность реальных инвестиционных проектов, можно измерить количественно.

В основе теории лежат следующие идеи: большинство инвесторов осторожны (не любят рисковать). При прочих равных условиях большинство инвесторов предпочитают высокие доходы низким. Следовательно, если только можно уменьшить риск, не уменьшая при этом ожидаемого дохода, инвесторы сделают попытку поступить именно так. Предположим, что среднеквадратическое отклонение доходности портфеля ценных бумаг можно считать разумно обоснованной мерой риска. Таким образом, существует стимул использовать диверсификацию для уменьшения среднеквадратического отклонения всего портфеля. Например, если два вида ценных бумаг характеризуются одинаковым ожидаемым уровнем доходности и независимы друг от друга, то можно показать, что риск портфеля, состоящего из ценных бумаг обоих видов, взятых в некоторой пропорции, будет более низким, чем риск портфеля, состоящего из ценных бумаг только одного вида.

До тех пор пока доходности различны, а ценные бумаги не слишком сильно коррелируют друг с другом, осторожные инвесторы могут уменьшить свой суммарный риск, диверсифицируя портфели. Однако в той мере, в какой доходности различных ценных бумаг не коррелируют и, таким образом, колеблются "в унисон", диверсификация не приводит к полному устранению риска.

Полезно было бы разделить риск на две части: 1) риск, который может быть устранен с помощью диверсификации, — он называется " несистематическим", 2) риск, который, несмотря ни на что, присущ даже эффективному портфелю (т. е. портфелю, который не подвержен диверсифицируемому несистематическому риску) — такой риск называется систематическим. Систематический риск показывает, как доходность инвестиционного портфеля коррелирует со среднерыночной.

Если затраты на диверсификацию относительно невелики, то инвесторы не захотят платить за ценные бумаги более высокую цену только потому, что данные активы несут сравнительно небольшую нагрузку диверсифицируемого риска (ведь его можно устранить путем диверсификации). Аналогично ценные бумаги, которые характеризуются высоким диверсифицируемым риском, не слишком сильно упадут в цене.

Согласно этой теории, в той мере, в которой котировки ценных бумаг определяются деятельностью инвесторов, которые могут диверсифицировать свои портфели с минимальными затратами, котировки установятся таким образом, что разницы ожидаемых уровней доходности будут отражать лишь разницу в размере систематического риска ценных бумаг.

Связь с моделью предпочтительного состояния. Модель САРМ можно рассматривать как частный случай модели предпочтительного состояния. Например, в "чистой" модели предпочтительного состояния активы характеризуются денежными потоками, которые они генерируют в каждом из возможных событий. Чтобы определить стоимость активов, нужно также знать коэффициенты текущей стоимости с поправкой на риск (RAPVF) для каждого состояния. Если предположить, что метод САРМ верен (или достаточно точен, чтобы его можно было применять на практике), то все, что нам нужно знать о каких бы то ни было активах, можно свести к двум параметрам: ожидаемому доходу, который будет получен в конце периода в результате владения активами, и их коэффициенту "бета". Богатство в конце периода состоит из денежных потоков, генерируемых активами в течение периода, и конечной стоимости самих активов. "Бета"- коэффициент, который рассмотрен далее в этой главе, показывает, в какой степени доход, накопленный к концу периода в результате владения активами, коррелирует с доходом, накопленным к концу периода в результате владения типичным для всей экономики видом активов. Далее речь будет идти об обобщенных концепциях САРМ, таких, как только что упомянутые. Будет показана также связь между обобщенными показателями и моделью предпочтительного состояния.

Исходные предпосылки. Чтобы понять метод САРМ и его ограничения, необходимо уяснить его исходные предпосылки. Эта модель рассчитана на один период, никаких предположений относительно изменения риска и доходности с течением времени нет. Предполагается, что инвестора интересует только ожидаемая доходность и среднеквадратическое отклонение или дисперсия исходов — доходов от портфеля. В этом недостаток теории, так как она игнорирует другую важную для большинства видов распределений вероятностей информацию, которую инвестор мог бы считать весьма существенной. Однако математического ожидания и дисперсии и в самом деле совершенно достаточно, чтобы знать все необходимые параметры нормального распределения вероятностей.

Предполагается, что только перспектива высокой доходности может заставить любого из инвесторов рисковать (т.е. инвесторы осторожны, не склонны к риску). Действия отдельного инвестора никак не отражаются на уровне цен. Инвесторы принимают цены такими, какими их устанавливает рынок (price-takers). Инвестор имеет возможность вложить деньги под процент, равный ставке по безрисковому вложению (rf), и в общем случае мы предполагаем, что он может брать взаем под тот же процент (от этого условия можно с легкостью отказаться). Инвесторы могут продавать ценные бумаги, которые им не принадлежат, т.е. они могут брать взаймы ценные бумаги с целью их продажи (это называется "продажа без покрытия на срок", или "короткая позиция" — short-sale). Все инвесторы имеют одно и то же мнение по поводу ожидаемой доходности и дисперсии всех ценных бумаг (их ожидания однородны, гомогенны), и все они полностью диверсифицируют свои вложения.

Количество ценных бумаг, которые можно купить, фиксировано и делимо (можно купить ценные бумаги на любую сумму в долларах). С заключением сделки не связаны никакие расходы и налоги.

Многие из этих допущений можно опустить и тем самым получить модель, более похожую на обычную модель САРМ. Мы выбрали именно такой набор исходных предположений для упрощения модели.

Введение в анализ портфеля. Модель оценки капитальных активов предполагает, что инвесторы принимают такие решения, которые касаются портфелей ценных бумаг в целом. Характеристики отдельно взятой ценной бумаги затрагивают инвестора только опосредованно, через их влияние на весь инвестиционный портфель. Перед тем как продолжить объяснение САРМ, дадим краткое описание принципов теории портфеля.

Пусть ri(s) — будущая доходность ценной бумаги типа i при условии, что возникнет событие s, и пусть р (s) — вероятность события s. Чтобы измерить последствия включения ценной бумаги i в портфель (или изменения доли ценной бумаги i в портфеле, если она там уже есть), необходимо знать ожидаемую доходность ценной бумаги i, дисперсию доходности и ее ковариацию с доходностью других ценных бумаг.

Ожидаемая доходность ценной бумаги i, обозначаемая Е(ri), определяется как средневзвешенная по всем вероятностям доходность при каждом из возможных событий

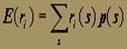
Дисперсия доходности, обозначаемая var(ri):

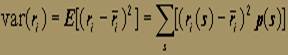
Среднеквадратическое отклонение, обозначаемое через s i, — это квадратный корень из дисперсии.

Ковариация доходностей ценных бумаг, обозначаемая cov(ri, rj) или s ij, это математическое ожидание произведения линейного отклонения доходностей ценных бумаг i и j от их математических ожиданий:

Ковариация показывает, как колеблются доходности двух ценных бумаг при различных условиях. Если при заданном состоянии s обе ценные бумаги характеризуются доходностью выше среднего или если доходность обеих бумаг ниже среднего, произведение линейных отклонений будет положительным. И наоборот, если в некоторых условиях доходность по одной ценной бумаге выше среднего, а по другой — ниже среднего, то произведение линейных отклонений будет отрицательным. Ковариация может быть положительной, отрицательной или нулевой, она зависит от относительной частоты возникновения этих состояний и размера отклонений. Для любых двух ценных бумаг положительная ковариация встречается значительно чаще, чем отрицательная. Коэффициент корреляции определяется как

Коэффициент корреляции может принимать значения от - 1 до +1.

Формирование портфеля. Портфели состоят из отдельных ценных бумаг или групп ценных бумаг, некоторым образом коррелирующих между собой. Пусть r1 и r2 — доходности двух ценных бумаг, а коэффициент корреляции между ними r. Если r = - 1, то ценные бумаги r1 и r2 находятся в отрицательной линейной зависимости, т.е. при увеличении r1 уменьшается r2 на точно известную величину. Если r >0, то корреляция положительная, но знание r1 не позволяет нам предсказать точную величину r2. Если r1 и r2 не коррелированы, то r = 0.

На рис. 3 по вертикальной оси отложена ожидаемая доходность ценных бумаг или портфеля, а по горизонтальной — среднеквадратическое отклонение доходности. Точка А соответствует ценной бумаге 1, точка В — ценной бумаге 2. Мы хотим узнать, что произойдет, если сформируем портфель, состоящий из обеих ценных бумаг, причем доля ценной бумаги 1 будет равна х1, а доля ценной бумаги 2 — х2, причем чтобы х1 + х2 = 1.

Для любого портфеля, состоящего из двух ценных бумаг, в котором доля инвестиций в ценную бумагу 1 равна х1, а доля инвестиций в ценную бумагу 2 — x2, причем x1 + x2 =1, выполняется:

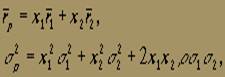
где 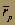— ожидаемая доходность портфеля, 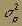- дисперсия доходности портфеля.

На рис. 6 показана ситуация, когда доходности активов А и В находятся в линейной зависимости (r = 1).

Если мы находимся в точке А, то это значит, что мы инвестировали 100% своих средств в активы вида А. По мере замены активов вида А на активы вида В мы движемся по прямой до точки В. Все комбинации активов А и В лежат на отрезке, соединяющем точки А и В.

0жидаемая доходность портфеля будет равна средневзвешенной между:

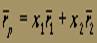
где х1 - доля инвестиций в актив 1, x2 - доля инвестиций в актив 2.

Среднеквадратическое отклонение доходности портфеля также равно средневзвешенной доходности активов:

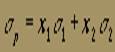
Рис. 6. Линейная зависимость между доходностями (r1 и r2) двух ценных бумаг А и В

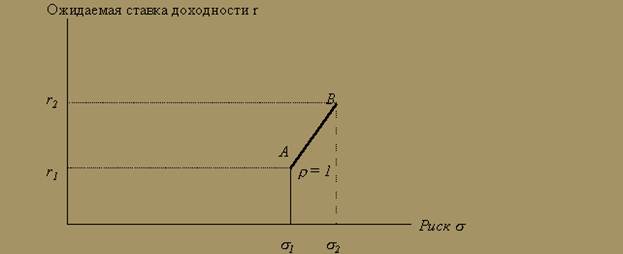
Такое упрощенное выражение для среднеквадратического отклонения можно использовать только при условии, что r =1.

Если коэффициент корреляции равен - 1, то активы связаны отрицательной линейной зависимостью. Рис. 7 показывает, что когда r = - 1, можно составить такой портфель, риск которого будет нулевым. Если портфель на 100% состоит из активов вида В, то мы находимся в точке В. По мере того как мы заменяем часть активов В на А, и риск, и ожидаемая доходность снижаются до тех пор, пока не достигнута точка С и риск портфеля не стал равным нулю. Если в портфель включается все больше активов типа А, инвестор катится вниз по отрезку СА. Риск увеличивается, ожидаемая доходность падает.

Любая точка отрезка СА доминирована одной или несколькими точками на отрезке СВ (т.е. во всех отношениях хуже их). Ни один инвестор не захочет иметь такое количество активов типа А, при котором его портфель находится на отрезке СА.

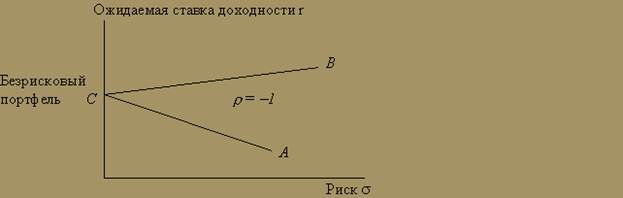
Рис. 7 Отрицательная линейная зависимость

Коэффициент корреляции может принимать значения от - 1 до +1. Рис.8 показывает область возможных портфелей при различной величине r. Если r = 0, то область допустимых портфелей — это кривая, проходящая внутри треугольника АВС. Если сначала все наши инвестиции состоят только из В, замена части активов В на активы А уменьшит риск. Если r < 0, то потенциал снижения риска еще выше. Это не удивительно: ведь риск А меньше, чем риск В.

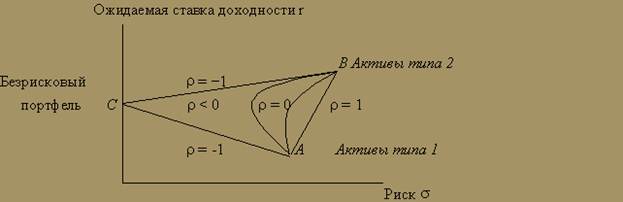
Рис.8. Две ценные бумаги и разные значения коэффициента корреляции r

Однако предположим, что сначала наш портфель полностью состоит из А, а затем мы добавили в него активы типа В, риск которых больше, чем риск А, и доходность выше, чем у А. Если r < 1, то существуют такие комбинации А и В, что доходность всего портфеля в целом выше, чем у А, а дисперсия ниже, чем у А. Поэтому любой инвестор, для которого полезность портфеля зависит только от ожидаемой доходности и дисперсии, предпочтет именно такой портфель. Это замечательный результат. Хотя ожидаемая доходность портфеля всегда не более чем средневзвешенная ожидаемых доходностей входящих в него ценных бумаг, дисперсия доходности всего портфеля может оказаться меньше, чем средняя из дисперсий его компонентов. Вот почему выгодна диверсификация.

В формировании портфеля область допустимых значений включает в себя все портфели, которые только можно сконструировать из доступных ценных бумаг. Если все доступные ценные бумаги рискованные (с ненулевой дисперсией), то область допустимых значений будет расположена справа от вертикальной оси или на оси (если коэффициент корреляции равен - 1, существует комбинация, расположенная на вертикальной оси). Если сделки с ценными бумагами без покрытия на срок не допускаются, то корреляция, равная в точности - 1, при обычных условиях на рынке акций будет невозможна.

Инвесторы. Осторожный инвестор хочет, чтобы ожидаемая доходность увеличивалась при увеличении риска (риск определен как дисперсия исходов).

Метод САРМ основан на предположении, что инвесторы, максимизирующие прибыль, 1) осторожны; 2) измеряют риск инвестиционного портфеля как дисперсию доходности инвестиционного портфеля и 3) их кривые безразличия (все комбинации ожидаемых доходностей и дисперсий, которые имеют одинаковую полезность для инвестора) имеют вид, показанный на рис. 9. По определению, любая точка на кривой безразличия U1 одинаково желательна для инвестора; следовательно, так как в точке В ожидаемая доходность выше, а риск такой же, как и в точке А, осторожный инвестор предпочтет точку В точке А. Наконец, точка В лежит на кривой безразличия U1, а все точки кривой U1 более предпочтительны, нежели точки кривой U0. Точка В предпочтительнее по сравнению с точкой С, так как ее ожидаемая доходность такая же, а риск меньше.

Анализ портфеля, состоящего из ценных бумаг, свободных от риска. До сих пор мы указывали, что инвестор, имеющий некоторые ожидания, должен определить для себя набор эффективных портфелей и затем выбрать из них тот, который лежит на кривой безразличия с наивысшей полезностью. Наши наблюдения касались только индивидуальных портфелей. У нас нет сведений о том, каким образом на рынке происходит обмен ожидаемой доходности на риск.

Рис.9. Кривая безразличия для двух инвесторов

Граница эффективности. На рис.10 показаны три портфеля. Ожидаемая доходность отложена по оси Y, а среднеквадратическое отклонение доходности — по оси X. На основе данных рис.10 заключаем, что:

1. портфель 2 предпочтительнее портфеля 1 (одинаковый риск и более высокая средняя доходность);

2. портфель 3 предпочтительнее портфеля 1 (одинаковая ожидаемая доходность при меньшем риске).

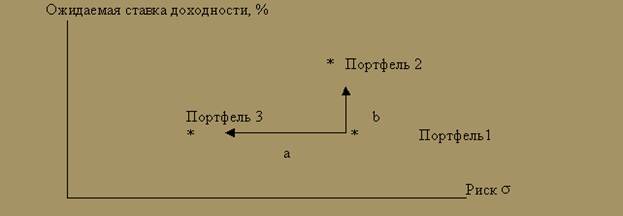
Рис. 10. Выбор портфелей

Любой портфель, расположенный в области, ограниченной векторами а и b, предпочтительнее, чем портфель 1. Полезность увеличивается, если двигаться вверх, налево или по диагонали вверх и налево. Если сравнивать портфели 2 и 3, то мы не сможем сделать окончательный выбор между ними. Доходность портфеля 2 выше, но и риск больше. Выбор будет зависеть от предпочтений инвесторов.

Если предположим, что существует ценная бумага, свободная от риска, и разовьем теорию портфеля дальше так, чтобы она охватывала и такую ситуацию, мы сможем глубже понять проблему. Правительственные облигации, которые инвесторы держат до момента погашения, по сути своей являются именно таким надежным активом. Таким образом, каждому инвестору доступна ценная бумага, свободная от риска. Здесь слова "свободная от риска" указывают только на отсутствие риска неуплаты, но не относятся к другим типам риска.

Рассмотрим свободную от риска ценную бумагу, процент по которой совпадает со стоимостью денег во времени (например, доходность казначейского векселя США за один период). Если приобретены два портфеля, один — состоящий только из ценных бумаг, свободных от риска, а другой — из более рискованных ценных бумаг, имеющих хождение на рынке (с параметрами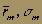), ожидаемая средняя доходность и среднеквадратическое отклонение различных портфелей будут расположены на прямой, проходящей через точки rf и М, как показано на рис. 11. Эта линия прямая потому, что коэффициент корреляции доходности ценной бумаги, свободной от риска, и доходности любой другой рискованной или свободной от риска ценной бумаги всегда равен нулю. Точка М — это точка касания прямой, проходящей через rf, с границей эффективности, определенной без учета безопасных активов. Хотя существуют и другие портфели, состоящие из комбинации эффективных портфелей и безрисковых активов (другие точки на границе эффективности ЕЕ), ни один из них не является столь же желательным, как портфели, расположенные на линии rf М. Линия rf М называется линией рынка капитала (capital market line).

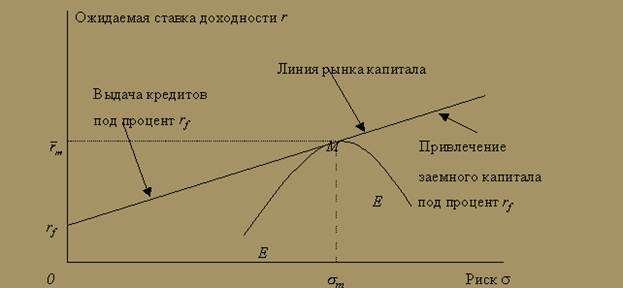
Рис.11. Линия рынка капитала и граница эффективности

Если инвестиционный портфель на 100% адекватен портфелю в точке М, то доходность вложений инвестора будет равна rm, а риск s m. Если часть активов портфеля М заменить на безопасные ценные бумаги, то отрезок rf М определяет область допустимых комбинаций ожидаемой доходности и риска.

Если инвестор пополняет инвестиционные ресурсы путем привлечения заемного капитала под процент, равный rf, и вкладывает полученные деньги в портфель М, то на луче, продолжающем отрезок rf М вправо, расположены все возможные комбинации ожидаемой доходности и риска. Так как капитал взят под процент rf и инвестирован под процент rm, где rm > rf, заем увеличивает ожидаемую прибыль, но и риск портфеля тоже растет.

Выберем точку на кривой ЕЕ, отличную от М. Заметьте, что при том же риске можно добиться и более высокой ожидаемой ставки доходности, если комбинировать портфель М и вложения в ценные бумаги, свободные от риска, находясь при этом на линии rf М. Линия rf М предлагает ряд инвестиционных возможностей, каждая из которых по крайней мере столь же желанна, как и любая точка на границе эффективности (как и любой набор инвестиционных возможностей, за исключением вложений в активы, свободные от риска).

Различные инвесторы (с разной степенью осторожности, с разным отношением к риску) будут держать оптимальные портфели, которые находятся в различных точках линии рынка капитала, но все оптимальные портфели будут состоять из комбинации активов, свободных от риска, и портфеля М, который называется рыночным портфелем (market portfolio).

Процесс выбора оптимального портфеля состоит из двух этапов. На первом этапе находят рыночный портфель — точку М. Если ожидания всех инвесторов совпадают, то все инвесторы будут держать часть одного и того же рыночного портфеля. Второй этап — нахождение оптимальной точки на линии rf M. Это оптимальная комбинация рыночного портфеля М и свободных от риска активов. Эти два этапа основаны на теореме о разделении (separation theorem), которую впервые предложил Тобин (Tobin).

Рыночный портфель состоит из всех видов рискованных активов, взятых в пропорции, соответствующей их доле на рынке. Общая цель всех инвесторов — достичь максимальной диверсификации, и они стремятся включить в свой портфель ценные бумаги всех видов, какие только есть. В понятие "ценная бумага" здесь включаются обыкновенные акции и все остальные ценные бумаги, которые имеют хождение на рынке. Таким образом, варранты, конвертируемые облигации, привилегированные акции тоже будут включены в портфель.

Принимая решение о размещении своих капиталов в активы, инвесторы не пытаются предсказать будущее изменение стоимости каждой отдельно взятой ценной бумаги, но используют уже готовые рыночные оценки. Таким образом, если доля обыкновенных акций компании Х в общем объеме всех акций на рынке составляет 0.35%, то акции Х должны составлять 0.35% той части инвестиционного портфеля, которая состоит из акций. Инвестор буквально покупает "кусочек рынка капитала". Получившийся в результате набор инвестиций будем называть рыночным портфелем.

САРМ предполагает, что вследствие высокой диверсифицированности рыночного портфеля и осторожности большинства инвесторов цены на ценные бумаги, входящие в рыночный портфель, находятся на таком уровне, что инвестор не может добиться более высокой доходности при том же или более низком уровне риска от каких бы то ни было иных инвестиций. Однако уровень риска рыночного портфеля может быть слишком высоким или слишком низким для конкретного инвестора. Инвесторы могут снизить рискованность своих вложений, продолжая инвестировать в рыночный портфель и дополнительно покупая активы, свободные от риска.

Вне зависимости от места расположения оптимального портфеля на графике каждый инвестор (кроме тех, что находятся на левой границе отрезка) компенсирует риск таким уровнем доходности, который соответствует углу наклона прямой, т.е. наклон кривой безразличия инвестора в точке касания с линией эффективного портфеля равен углу наклона прямой. Такой предельный уровень доходности, представляющий собой компромисс между риском и доходом, равен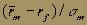. Такое компромиссное решение доступно каждому инвестору.

Если инвестор может брать в долг под процент rf и согласен подвергать себя риску, большему, чем s m, то состояние его описывается движением вверх по лучу, продолжающему отрезок rf М. Использует ли инвестор заемный капитал (движение вправо от точки М) или вкладывает капитал в ценные бумаги, свободные от риска (движение влево от точки М), — зависит от его склонности к риску. Но все инвесторы будут держать рыночный портфель за исключением тех, что купят только активы, свободные от риска.

При выборе портфеля были использованы два критерия: ожидаемая доходность и среднеквадратическое отклонение портфеля. Рассматривая риск конкретной ценной бумаги, в качестве меры риска мы выберем ковариацию доходности по этой ценной бумаге и доходности рыночного портфеля.

Линия рынка капитала. Пусть rf представляет собой процент, который можно заработать на государственных ценных бумагах со сроком погашения через 1 период. Для инвестора, горизонт планирования которого равен одному периоду, приобретение государственных ценных бумаг сроком на один период не будет связано с риском невозврата капитала. Назовем такие государственные ценные бумаги "безрисковыми активами" (default-free asset), так как мы рассматриваем исключительно риск неуплаты. Теперь рассмотрим возможные портфели, которые можно было бы составить, комбинируя рыночный портфель с такими государственными ценными бумагами. Пусть наш воображаемый инвестор вложил долю a своих активов в рыночный портфель и долю (1 - a) - в государственные ценные бумаги. Пусть a > 0. Обозначим через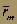, ожидаемую доходность на каждый вложенный в рыночный портфель доллар. Аналогично пусть s m обозначает среднеквадратическое отклонение доходности rm, рыночного портфеля. Тогда ожидаемая доходность инвестиционного портфеля 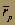задана уравнением:

(1)

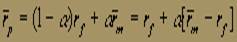
а среднеквадратическое отклонение — выражением:

(2)

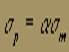
Решив второе уравнение относительно a и подставив полученное выражение в формулу (1), соотношение ожидаемой доходности портфеля и его среднеквадратическое отклонение можно переписать так:

(3)

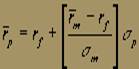
Графическое представление уравнения (3) дано на рис.12. Линия AD — это линия рынка капитала.

Если инвестор выбирает a = 0, все его средства будут вложены в государственные ценные бумаги и ожидаемая доходность составит rf, а s p = 0. Это соответствует точке А на рис.9. Если инвестор выберет a = 1, то весь его капитал будет вложен в рыночный портфель и ожидаемая доходность будет равна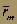, а s p = s m. Это соответствует точке С на рис.9. Инвестор мог бы также оказаться в любой точке отрезка АС, выбирая соответствующие a в интервале между 0 и 1. Точки справа от С на линии рынка капитала соответствуют величине a > 1.Чтобы достичь одной из этих точек, у инвестора должна быть возможность брать взаймы под процент, равный rf. Пусть дела обстоят именно таким образом и инвестор хочет, чтобы уровень риска соответствовал s p = 2s m. Инвестор может купить на два доллара ценных бумаг в расчете на каждый доллар собственного капитала. Необходимый для этого капитал можно взять в долг. В результате инвестор купит рыночный портфель, приносящий доходность rf, оплатив лишь 50% его стоимости из своего кармана. Ожидаемую доходность для инвестора можно найти из уравнения (1) при a = 2. Аналогично среднеквадратическое отклонение портфеля получится, если подставить a = 2 в уравнение (2). Так как оба уравнения выполняются, выполняется и уравнение (3).

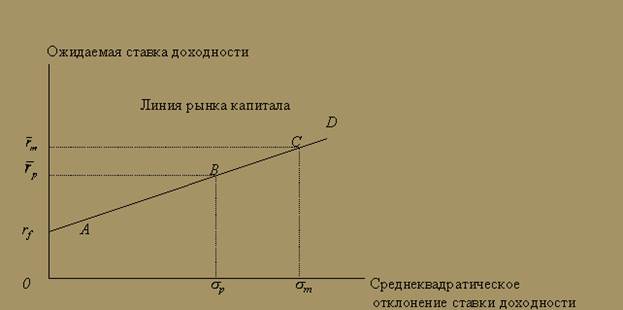
Рис.12. Линия рынка капитала

Линия рынка капитала применима только для особой категории портфелей: для таких, которые состоят из комбинации рыночного портфеля и активов, свободных от риска.

Ожидаемая доходность ценных бумаг. Пусть инвестор держит рыночный портфель. Поскольку рынок находится в состоянии равновесия, то при добавлении в этот портфель малой доли новой ценной бумаги i ожидаемое соотношение между риском и доходностью должно соответствовать соотношению риска и доходности на рынке в настоящий момент. Можно показать, что необходимое условие для этого заключается в том, чтобы ожидаемая доходность i была равна

(4)

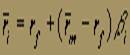
где - ожидаемая равновесная ставка доходности ценной бумаги i;

rf - ставка доходности по безрисковым вложениям;

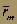- ожидаемая среднерыночная ставка доходности;

b i - коэффициент "бета" ценной бумаги i (мера риска):

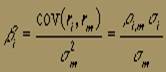
Слагаемое - это корректировка на риск по сравнению с доходностью ценной бумаги rf, свободной от риска.

Коэффициент "бета" измеряет величину систематического риска, т.е. риска, возникающего в результате колебаний доходности на всем рынке ценных бумаг. В модели САРМ нет никакой корректировки на риск отдельной фирмы (несистематический), так как предполагается, что диверсифицированный риск стремится к нулю при очень большом количестве различных видов инвестиций (несистематические компоненты независимы).

"Бета" - коэффициент ценной бумаги, показывает, как доходность ценной бумаги коррелирует со средней рыночной доходностью: это показатель меры систематического риска ценной бумаги.

Линия характеристик ценных бумаг. Избыточная доходность рыночного портфеля по сравнению с инвестициями в абсолютно надежные ценные бумаги равна rm - rf. Избыточная доходность инвестиций в ценные бумаги типа i по сравнению со средним уровнем равна ri - rf. Если избыточную доходность ценной бумаги i отложить по одной оси, а избыточную среднерыночную доходность — по другой, то получим график характеристик ценной бумаги (рис. 13). Такой график можно начертить для любой ценной бумаги или любого портфеля ценных бумаг. Угол наклона прямой равен b i, - коэффициенту ценной бумаги i, а отрезок, отсекаемый линией на вертикальной оси, равен a i.

Коэффициент a ценной бумаги - это избыточная доходность ценной бумаги по сравнению с доходностью ценной бумаги, свободной от риска, в случае, когда доходность рыночного портфеля равна доходности по ценным бумагам, свободным от риска (т.е. избыточная доходность на рынке нулевая). Когда избыточная доходность на рынке равна 0, мы вправе ожидать, что каждая ценная бумага в состоянии рыночного равновесия также будет иметь нулевую избыточную доходность (a = 0). В то время как средневзвешенная (a -коэффициентов всех ценных бумаг равна 0, a некоторых ценных бумаг положительна, а некоторых — отрицательна, в зависимости от фактически наблюдаемой ставки доходности.

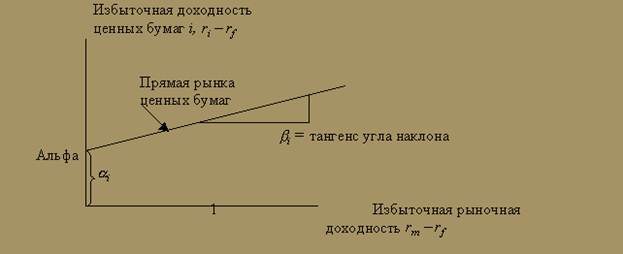
Рис.13. Линия характеристик ценной бумаги

Если рынок считает, что те условия, которые привели к тому, что а оказалась положительной, в будущем сохранятся, то ценная бумага становится привлекательной. Ее будут покупать и цена её вырастет, а доходность упадет, так что ожидаемый коэффициент a окажется равным 0. Так как рынок несовершенен (да и прогнозы не идеальны), не удивительно, что когда через некоторое время начинают чертить график фактической доходности, оказывается, что a -коэффициент ценной бумаги не равен в точности 0. Если мы считаем, что рынок находится в состоянии равновесия, то наиболее вероятная оценка уровня a -коэффициента ценной бумаги равна 0, но если фактическая a, вычисленная на основе графика избыточной доходности, будет равна 0, то это окажется большим сюрпризом.

Поскольку САРМ пренебрегает важными факторами, которые инвесторы на практике принимают во внимание, можно ожидать, что в результате воздействия этих неучтенных факторов a -коэффициенты всех ценных бумаг (или классы ценных бумаг) будут либо положительными, либо отрицательными. Например, обыкновенные акции энергетической компании, строящей АЭС, могут иметь отрицательный a -коэффициент, так как САРМ не учитывает особые виды риска, связанные со строительством АЭС, а рынок обязательно примет их во внимание.

Иногда считают, что коэффициент b подходит для измерения риска акции. Коэффициент сравнивает корреляцию рыночной доходности и доходности конкретной акции (r i, m), среднеквадратическое отклонение акции (s i) со среднеквадратическим отклонением рыночного портфеля (s m). b коэффициент портфеля равен средневзвешенной b -коэффициентов его компонентов:

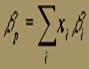
Дата добавления: 2014-01-05