Модели материала

Основными конструкционными материалами в машиностроении являются сплавы чёрных и цветных металлов. Используются также различные неорганические и органические материалы (полимеры, пластмассы, керамика). В последнее время нашли применения композиционные материалы, состоящие из высокопрочных нитей стекла, бора, углерода и связующего полимера.

Металлы имеют поликристаллическое (зернистое) строение. Но инженерные модели материала наделяют его следующими свойствами: однородность, сплошность, упругость, изотропность.

Однородность понимается в том смысле, что все неоднородные структурные дискретные элементы заменяются «осредненной» непрерывной средой. Свойства не зависят от величины выделенного из тела объёма.

Сплошность понимается в том смысле, что материал заполняет весь объем тела без пустот, раковин и прочих дефектов. Хотя эти дефекты вполне возможны в реальных деталях.

Упругость – это способность тела восстанавливать свои первоначальные размеры после снятия нагрузки.

Изотропность – это независимость механических свойств от направления нагрузки. Материалы, не обладающие этим свойством, называются анизотропными (древесина, композиты на основе стеклоткани).

В подавляющем большинстве случаев такая модель вполне адекватно отражает свойства реальных конструкционных материалов. Однако иногда такая модель становится недостаточной и приходится принимать более сложную модель: материал наделяют свойствами пластичности и ползучести. Пластичностью называется свойство тела сохранять после прекращения действия нагрузки полученную при нагружении деформацию (например, изгиб медной проволоки). Ползучестью называется свойство тела увеличивать деформацию при постоянных внешних нагрузках (например, осадка фундамента или ослабление затяжки болтов вследствие их удлинения со временем).

1.2.2. Модели формы

Основными моделями формы в моделях прочностной надёжности являются: стержни, пластинки, оболочки, пространственные тела (массивы).

Стержнем (или брусом) называется тело, поперечные размеры которого малы по сравнению с его длиной (рис.1.1).

Образование стержня можно представить как результат движения вдоль прямой или пространственной кривой (оси стержня) плоской фигуры (поперечного сечения стержня). Поперечное сечение стержня может быть переменным по длине. При движении вдоль оси оно может поворачиваться и тогда стержень называется закрученным. Стержневой модели соответствует колоссальное количество реальных деталей и конструкций: колонны зданий, подкрановые балки, мосты, телебашня, валы турбин, двигателей внутреннего сгорания, редукторов, электродвигателей, лопатки компрессоров, паровых и газовых турбин (закрученные стержни переменного сечения) и т.д.

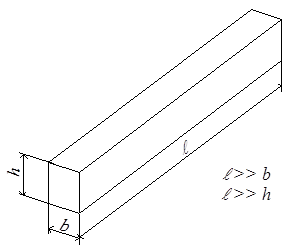
Рис. 1.1

Пластиной называется тело, ограниченное двумя плоскими или слабоизогнутыми поверхностями (рис.1.2). Толщина пластины много меньше двух других размеров. Схеме пластины соответствуют плиты междуэтажных перекрытий, диски турбин и т.д.

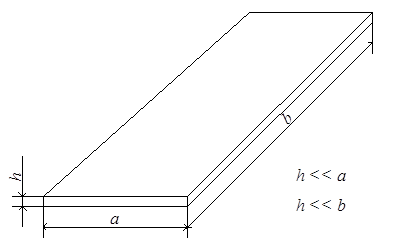
Рис. 1.2

Оболочкой называется тело, ограниченное двумя близкими криволинейными поверхностями. Расстояние между поверхностями – толщина оболочки – мало по сравнению с радиусами кривизны поверхностей (рис.1.3). Оболочечной моделью описывается столь же большее количество конструкций, что и стержневой. Это трубопроводы, сосуды для хранения жидкостей и газов, корпуса химических аппаратов, кузова автомобилей и железнодорожных вагонов, корпуса самолётов и ракет, перекрытия концертных залов и стадионов и т.д.

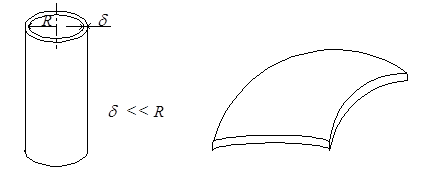
Замкнутая цилиндрическая оболочка Незамкнутая оболочка

Рис.1.3

Массивом называется тело, у которого все размеры одного порядка. Это могут быть элементы деталей машин (проушины, головки болтов, стержни с выточками или отверстиями). Этой модели соответствует значительно меньшее количество конструкций, чем стержневой или оболочечной (рис.1.4).

Рис.1.4. Плотина

Модели нагружения имеют существенное значение для расчётов на прочность, поэтому рассмотрим их отдельно.

1.3. Классификация сил (модели нагружения)

При рассмотрении любой детали или сооружения взаимодействие с окружающими ее элементами и воздействие внешней среды характеризуется внешними силами. Классификация их представлена на рис.1.5.

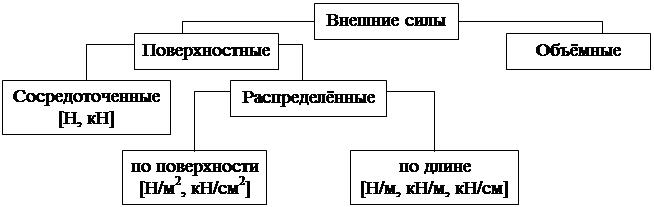Рис.1.5

1кгс = 9,81Н» 10Н; 1Н/м² = 1Па;

1тс = 9,8кН» 10кН; 10⁶Па = 1МПа.

Сосредоточенные силы – силы, действующие на небольших участках поверхности деталей (например, давление колеса на рельсы, давление моста на опору).

Распределённые силы – силы, приложенные к значительным участкам поверхности (например, давление жидкости или газа на стенки сосуда).

Объёмные или массовые силы – силы, приложенные к каждой частице материала (например, силы тяжести или силы инерции).

Важным моментом при разработке модели нагружения является учёт характера изменения внешних сил по времени. Классификация на рис.1.6.

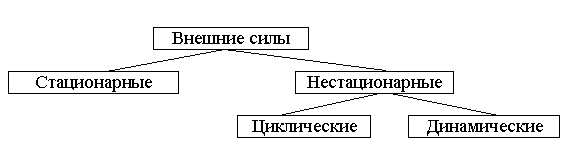
Рис.1.6

Стационарные или статические силы нагружают конструкцию медленно, постепенно возрастая от нуля до своего конечного значения. По достижении конечного значения не меняются. Ускорения элементов конструкций равны нулю.

Циклические или повторно – переменные нагрузки многократно меняют свою величину и направление по периодическому закону. Такие нагрузки испытывают вращающиеся валы машин.

Динамические нагрузки меняют свою величину в течение малого промежутка времени и сопровождаются значительными ускорениями, например, ударное нагружение, возникающее вследствие резкой остановки вращающегося массивного вала машины.

а б

Деталь Отсечённая часть детали

Рис.1.7

Детали находятся в равновесии под воздействием приложенных к ним внешних сил (рис.1.7,а). Реакции опор также относятся к внешним силам. Взаимодействие между частями рассматриваемой детали характеризуется внутренними силами. Чтобы обнаружить внутренние силы, необходимо провести плоскость, которая рассечёт деталь на две части и рассмотреть равновесие любой из них (рис.1.7,б)

Внутренние силы в сечении П представляют собой силы взаимодействия между частицами материала. Из условий равновесия (1.1.) отсечённой части тела можно определить составляющие главного вектора и главного момента внутренних сил, действующих в сечении П. В этом состоит сущность метода сечения – одного из важных методов сопротивления материалов.

∑х = 0, ∑у = 0, ∑z = 0, ∑M_x = 0, ∑M_y = 0, ∑M_z = 0. (1.1)

Составляющие (компоненты) внутренних сил имеют следующие названия:

N_x – продольная сила;

Q_y и Q_z – поперечные силы;

M_x – крутящий момент;

M_y и M_z – изгибающие моменты.

Распределение внутренних усилий по сечению заранее неизвестно, определение его составляет одну из главных задач сопротивления материалов.

1.4. Напряжения

Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. Интенсивность внутренних сил измеряется напряжением.

Пусть на малую площадку ∆F, расположенную в окрестностях точки А сечения П, действует сила ∆P (рис.1.8,а).

а б

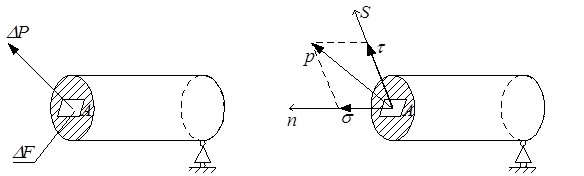
Сила в точке А Напряжения в точке А

Рис.1.8

Напряжение p в точке А рассматриваемого сечения определяется по формуле

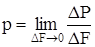. (1.2)

Вектор напряжения р совпадает с вектором усилия ∆Р. Как всякий вектор он может быть представлен нормальной (по отношению к площадке) составляющей σ и касательной составляющей τ (рис.1.8,б). Экспериментальными исследованиями установлено, что влияние нормальных и касательных напряжений на прочность различно, и поэтому в дальнейшем окажется необходимым всегда раздельно рассматривать составляющие вектора напряжений.

Итак, напряжение – это величина внутренней силы, приходящейся на единицу площади сечения в данной точке: σ – нормальное напряжение, τ – касательное напряжение, p – полное напряжение. Напряжение имеет размерность

.

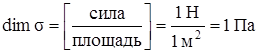Так как паскаль – очень маленькая величина, практические расчёты ведут в мегапаскалях или в килоньютонах на квадратный сантиметр: 10⁶ Па = 1 МПа, 10 МПа = 1 кН/см².

Напряжения в разных точках сечения могут быть различными. Величина напряжения меняется не только от точки к точке, но зависит и от ориентации площадки. Каждой площадке будет соответствовать определенное значение составляющих напряжений. Совокупность всех этих напряжений характеризует напряжённое состояние в точке.

1.5. Общие принципы расчёта на прочность

Целью расчёта является выяснение вопроса – удовлетворяет ли конструкция (деталь) требованиям надёжности, которые к ней предъявляются.

Надёжностью называется свойство изделия выполнять заданные функции, сохраняя свои эксплуатационные показатели в определённых пределах в течение требуемого промежутка времени или наработки,

Прочностной надёжностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.

В машиностроении в качестве параметра работоспособности изделий, как правило, используют напряжение. Поэтому метод расчёта на прочность называется расчётом по допускаемым напряжениям. Порядок расчёта следующий:

1.Определение внешних нагрузок, составление расчётной схемы.

2.Определение внутренних усилий и характера их изменения. Нахождение положения опасного сечения.

3.Определение величины и характера распределения напряжений в опасном сечении. Нахождение опасной точки и определение величины наибольшего напряжения σ_max или, в случае сложного напряжённого состояния, величины наибольшего расчётного напряжения σ_расч.

4.Определение величины допускаемого напряжения [σ] по формуле

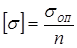, (1.3)

где σ₀ – опасное напряжение, соответствующее наступлению предельного состояния для данного материала, находится при лабораторных испытаниях;

n – коэффициент запаса прочности, n > 1.

5.Проверка условия прочности

σ_max ≤ [σ]. (1.4)

При определении допускаемого напряжения [σ] по формуле (1.3) очень важно правильно выбрать модель разрушения и обоснованно назначить запас прочности. Модель разрушения зависит от материала и условий нагружения детали. Может быть статическое разрушение, длительное статическое разрушение, усталостное разрушение, малоцикловое разрушение.

Глава 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ – СЖАТИЕ ПРЯМОГО БРУСА

2.1. Усилия и напряжения в поперечном сечении бруса

Растяжение и сжатие весьма часто встречаются в элементах строительных конструкций и машин.

Если внутренние силы в поперечном сечении стержня сводятся только к одному силовому фактору – продольной силе N, а все остальные внутренние силы равны нулю, то имеет место центральное растяжение или сжатие.

Внешние силы, вызывающие растяжение или сжатие, приложенные к концевым или промежуточным сечениям стержня, должны быть также направлены по его оси или приводиться к равнодействующей, направленной по этой оси.

Рассмотрим растянутый стержень (рис.2.1). Передача сил Р на этот стержень может быть осуществлена различными способами: можно, например, отогнуть концы стержня и захватить его за образовавшуюся петлю, можно изготовить стержень с бортиками и передать усилия через выступ, можно нарезать резьбу, можно сделать отверстие и в отверстие вставить палец, словом, вариантов можно предложить много. Всем этим, отличающимся друг от друга конструкциям, может быть поставлена в соответствие одна и та же расчётная схема (рис.2.2). Это возможно благодаря справедливости принципа Сен-Венана, названному по имени предложившего его французского учёного, сыгравшего большую роль в создании сопротивления материалов и теории упругости в середине XIX века.

Рис.2.1

Принцип Сен-Венана утверждает следующее: особенности приложения внешних сил сказываются на расстоянии, не превышающем характерный размер поперечного сечения. Напряжения и деформации в стержне на достаточном удалении от мест захвата (равном характерному размеру поперечного сечения – диаметру d) будут одинаковы, если одинаковы приложенные силы. Применение принципа Сен-Венана позволяет существенно расширить общность основных расчётных формул сопротивления материалов, поскольку освобождает от необходимости учитывать конкретные особенности местного распределения сил.

Для определения продольных сил применяется метод сечений, который заключается в том, что стержень мысленно пересекается плоскостью, перпендикулярной оси стержня, на две части. Продольная сила N равна сумме проекций на ось стержня сил, действующих по одну сторону от сечения. Сила N считается положительной, если она вызывает растяжение (направлена от сечения), и отрицательной, если она вызывает сжатие (направлена к сечению).

Рассмотрим расчётную схему стержня (рис.2.2). Стержень рассекаем сечением m-n и рассматриваем равновесие левой отсечённой части. Целесообразно неизвестную продольную силу N принимать положительной (растягивающей). Если при решении уравнения статики сила N получится со знаком “–“, то её направление надо поменять на противоположное и учитывать в дальнейшем расчёте, что стержень сжат. В нашем случае (рис.2.2.) получим N = P, т.е. стержень растянут: ∑x = 0, N – P = 0, N = P.

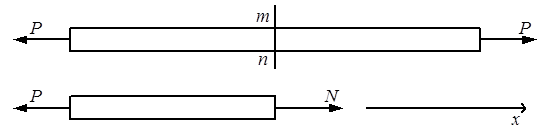
Рис.2.2.

В более сложных случаях нагружения стержня имеет смысл строить график изменения продольных сил по длине, называемый эпюрой продольных сил. На рис.2.3 изображен брус, находящийся под действием внешних сил, направленных вдоль оси. Показана эпюра продольных сил.

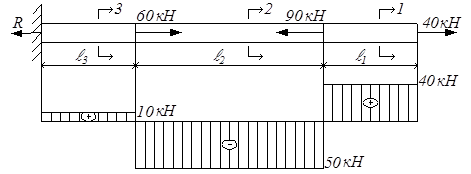
Рис.2.3

При построении эпюры N рассматривали равновесие отсечённых частей на каждом из участков ℓ₁, ℓ₂, ℓ₃ (рис.2.4).

∑х = 0: 40 – N1 = 0, N1 = 40 кН;   ∑х = 0: 40 – 90 – N2 = 0, N2 = – 50 кН;   ∑х = 0: 40 – 90 + 60 – N3 = 0, N3 = 10 кН.

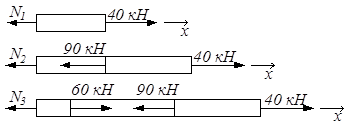
Рис.2.4

Из рис.2.4 следует, что мы все время рассматривали равновесие правой отсечённой части. Это связано с тем обстоятельством, что мы не определили реакцию опоры R, которая относится к внешним силам. Если бы сначала нашли R из уравнения статики, можно было бы рассматривать равновесие и левой отсечённой части. Построив эпюру N, получили R = 10 кH (растяжение).

С помощью построенной эпюры легко установить значение N, необходимое для расчёта на прочность. Так, в нашем примере получили½N_max½ = 50кН. Это значение не совпадает ни с одной из внешних сил.

Продольная сила N, возникающая в поперечном сечении бруса, представляет собой равнодействующую внутренних нормальных сил, распределённых по площади поперечного сечения и связана с возникающими в этом сечении нормальными напряжениями зависимостью:

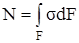, (2.1)

где σ – нормальное напряжение в произвольной точке поперечного сечения, принадлежащей элементарной площадке dF;

F – площадь поперечного сечения бруса.

Однако из формулы (2.1) нельзя найти закон распределения нормальных напряжений σ по площади поперечного сечения. Опыты показывают, что если нанести на поверхность бруса систему линий перпендикулярных оси бруса (рис.2.5), то после нагружения поперечные линии a-a, b-b, c-c, d-d переместятся параллельно самим себе.

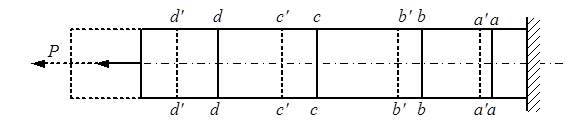
Рис 2.5.

Каждую такую линию можно рассматривать как след плоскости поперечного сечения бруса, – это позволяет считать, что поперечные сечения бруса, плоские до его нагружения, остаются плоскими и при действии нагрузки. Выполняется гипотеза плоских сечений, впервые предложенная голландским учёным Д. Бернулли и широко применяемая в задачах сопротивления материалов: удлинения и напряжения во всех точках поперечного сечения бруса равны между собой, что позволяет в выражении (2.1) вывести величину σ за знак интеграла. Таким образом,

,

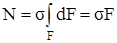откуда

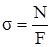. (2.2)

Итак, в поперечных сечениях бруса при его растяжении (или сжатии) возникают равномерно распределённые нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.

2.2. Условие прочности

Для решения вопроса о прочности, в соответствии с принятым методом расчёта на прочность по допускаемым на­пряжениям и условием прочности (1.4), запишем это условие применительно к растянутому (сжатому) стержню.

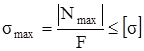, (2.3)

где |N_max| – максимальная по абсолютному значению продольная сила;

F – пло­щадь поперечного сечения стержня;

[σ] – допускаемое напряжение.

При реше­нии задач сопротивления материалов [σ] всегда задано. При расчётах машин или конструкций Нормы расчёта дают указания по поводу назначения или расчёта [σ]. Формула (2.3) применима для стержня из материала, имею­щего одинаковую прочность на растяжение и на сжатие (например, для стали). Но если материал по-разному сопротивляется растяжению и сжатию (напри­мер, чугун) для расчёта на прочность необходимо учитывать знак продольной силы и записывать два условия прочности

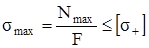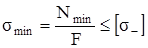, , (2.4)

где N_max – наибольшая (растягивающая) продольная сила;

N_min – наименьшая (сжимающая) продольная сила;

[σ₊] и [σ_-] – допускаемые напряжения на растяжение и на сжатие соответственно.

Значение N, входящее в условие прочности, определяется предварительно по эпюре N (рис.2.3.) или из расчёта статического равновесия конструкции.

Рассмотрим пример. Необходимо определить размеры поперечного сечения стержней кронштейна, удерживающего нагрузку P = 100 кН (рис.2.6).

Стержень №1: стальной, круглый, [σ] = 160 МПа; стержень №2: деревянный, квадратный, [σ] = 12 МПа.

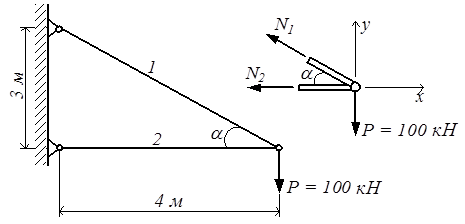
Рис.2.6

Сначала найдём усилия в стержнях. Для такой системы можно записать два уравнения статики:

∑ х = 0: – N₂ – N₁cos α = 0,

∑ y = 0: – P + N₁sin α = 0.

.

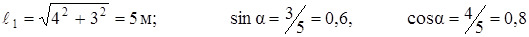Из уравнения ∑ y = 0 найдём .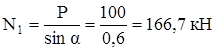

Из уравнения ∑ х = 0 найдём N₂ = – N₁cos α = – 166,7 ∙ 0,8 = – 133,3 кН.

Из условия прочности 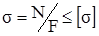найдём площади поперечного сечения стержней

, .

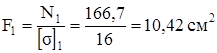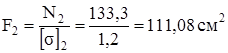При расчётах прочности величину допускаемого напряжения, заданную в МПа, перевели в кН/см²: 160 МПа = 16 кН/см² и 12 МПа = 1,2 кН/см². Теперь осталось определить размеры поперечных сечений.

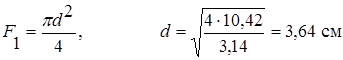
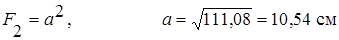
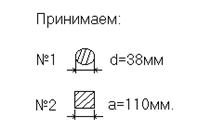
2.3. Деформации. Закон Гука

Рассмотрим деформации, возникающие при растяжении и сжатии стержней. При растяжении длина стержня увеличивается, а поперечные размеры сокра­щаются. При сжатии, наоборот, длина стержня уменьшается, а поперечные размеры увеличиваются. На рис.2.7 пунктиром показан деформированный вид растянутого стержня.

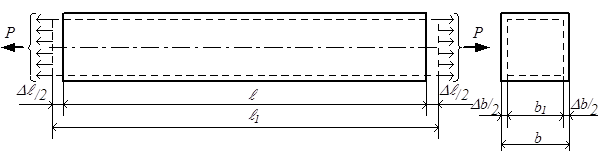
Рис.2.7

ℓ – длина стержня до приложения нагрузки;

ℓ₁ – длина стержня после приложения нагрузки;

b – поперечный размер до приложения нагрузки;

b₁ – поперечный размер после приложения нагрузки.

Абсолютная продольная деформация ∆ℓ = ℓ₁ – ℓ.

Абсолютная поперечная деформация ∆b = b₁ – b.

Значение относительной линейной деформации ε можно определить как отношение абсолютного удлинения ∆ℓ к первоначальной длине бруса ℓ

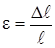. (2.5)

Аналогично находятся поперечные деформации

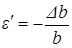. (2.6)

При растяжении поперечные размеры уменьшаются: ε > 0, ε′ < 0; при сжатии: ε < 0, ε′ > 0. Опыт показывает, что при упругих деформациях поперечная всегда прямо пропорциональна продольной.

ε′ = – νε. (2.7)

Коэффициент пропорциональности ν называется коэффициентом Пуассона или коэффициентом поперечной деформации. Он представляет собой абсолютную величину отношения поперечной деформации к продольной при осевом растяжении

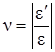. (2.8)

Назван по имени французского учёного, впервые предложившего его в начале XIX века. Коэффициент Пуассона есть величина постоянная для материала в пределах упругих деформаций (т.е. деформаций, исчезающих после снятия нагрузки). Для различных материалов коэффициент Пуассона изменяется в пределах 0 ≤ ν ≤ 0,5: для стали ν = 0,28…0,32; для резины ν = 0,5; для пробки ν = 0.

Между напряжениями и упругими деформациями существует зависимость, известная под названием закон Гука:

σ = Еε. (2.9)

Коэффициент пропорциональности Е между напряжением и деформацией называется модулем нормальной упругости или модулем Юнга. Размерность Е такая же, как и у напряжения. Так же, как и ν, Е – упругая постоянная материала. Чем больше значение Е, тем меньше, при прочих равных условиях, продольная деформация. Для стали Е = (2...2,2)10⁵ МПа или Е = (2...2,2)10⁴ кН/см².

Подставляя в формулу (2.9) значение σ по формуле (2.2) и ε по формуле (2.5), получим выражение для абсолютной деформации

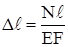. (2.10)

Произведение EF называется жёсткостью бруса при растяжении и сжатии.

Формулы (2.9) и (2.10) – это разные формы записи закона Гука, предложенного в середине XVII века. Современная форма записи этого фундаментального закона физики появилась гораздо позже – в начале XIX века.

Формула (2.10) справедлива лишь в пределах тех участков, где сила N и жёсткость EF постоянны. Для ступенчатого стержня и стержня, нагруженного несколькими силами, удлинения подсчитываются по участкам с постоянными N и F и результаты суммируются алгебраически

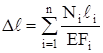. (2.11)

Если эти величины изменяются по непрерывному закону, ∆ℓ вычисляется по формуле

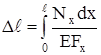. (2.12)

В ряде случаев для обеспечения нормальной работы машин и сооружений размеры их деталей должны быть выбраны так, чтобы кроме условия прочности обеспечивалось условие жёсткости

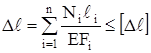, (2.13)

где ∆ℓ – изменение размеров детали;

[∆ℓ] – допускаемая величина этого изменения.

Подчёркиваем, что расчет на жёсткость всегда дополняет расчёт на прочность.

2.4. Расчёт стержня с учетом собственного веса

Простейшим примером задачи о растяжении стержня с переменными по длине параметрами является задача о растяжении призматического стержня под действием собственного веса (рис.2.8,а). Продольная сила N_x в поперечном сечении этого бруса (на расстоянии x от его нижнего конца) равна силе тяжести нижележащей части бруса (рис.2.8,б), т.е.

N_x = γFx, (2.14)

где γ – удельный вес материала стержня.

. (2.15)

Продольная сила и напряжения меняются по линейному закону, достигая максимума в заделке. Осевое перемещение произвольного сечения равно удлинению вышерасположенной части бруса. Поэтому определить его нужно по формуле (2.12), интегрирование вести от текущего значения х до х = ℓ:

.

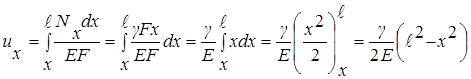Получили выражение для произвольного сечения стержня

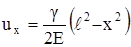. (2.16)

При х = 0 перемещение наибольшее, оно равно удлинению стержня

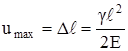. (2.17)

На рис.2.8,в,г,д приведены графики N_x, σ_х и u_x

а б в г д

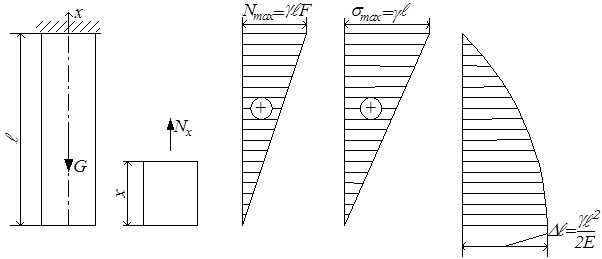
Рис.2.8

Умножим числитель и знаменатель формулы (2.17) на F и получим:

.

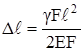Выражение γFℓ равно собственному весу стержня G. Поэтому

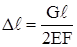. (2.18)

Формула (2.18) может быть сразу получена из (2.10)., если помнить, что равнодействующая собственного веса G должна быть приложена в центре тяжести стержня и поэтому она вызывает удлинение только верхней половины стержня (рис.2.8,а).

Если стержни, кроме собственного веса, нагружены ещё сосредоточенными продольными силами, то напряжения и деформации определяют на основе принципа независимости действия сил отдельно от сосредоточенных сил и от собственного веса, после чего результаты складывают.

Принцип независимости действия сил вытекает из линейной деформируемости упругих тел. Суть его заключается в том, что любая величина (напряжение, перемещение, деформация) от действия группы сил может быть получена как сумма величин, найденных от каждой силы в отдельности.

2.5. Статически неопределимые системы

Мы рассмотрели два примера, в которых внутренние усилия в стержнях определялись из уравнений статики. Это были статически определимые системы.

Статически определимыми называются системы, у которых число неизвестных реакций (число внутренних силовых факторов) равно числу уравнений статики.

Рассмотренные конструкции легко можно переделать – с целью повышения прочности установить дополнительную опору или дополнительный стержень (рис.2.9).

а б

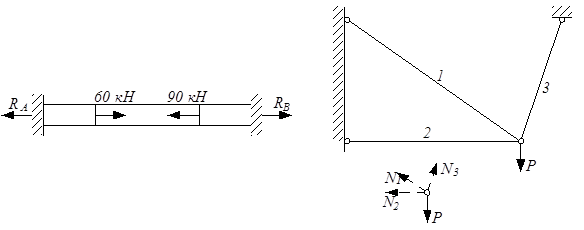
Рис.2.9

При этом увеличивается число неизвестных усилий, а число уравнений статики остается неизменным. Так, для стержня на рис.2.9,а невозможно найти две неизвестных опорных реакции R_A и R_В (и, соответственно, продольную силу N на каждом из трёх участков) из единственного уравнения статики ∑ х = 0. А для кронштейна на рис.2.9,б невозможно найти усилия в стержнях N₁, N₂ и N₃ из двух уравнений статики. Конструкции стали статически неопределимыми.

Статически неопределимыми называются системы, у которых число неизвестных реакций (число внутренних силовых факторов) превышает число уравнений статики. Разность между числом неизвестных усилий и числом независимых уравнений статики называется степенью статической неопределимости. Её можно найти из таких соображений: степень статической неопределимости равна числу “лишних” связей – связей, которые можно удалить из конструкций без ущерба для статического равновесия. Например, абсолютно жёсткий брус АВ закреплен на шарнирной опоре А и удерживается четырьмя тягами (рис.2.10). Равновесие бруса АВ не будет нарушено, если из четырех тяг удалить три. Если же удалить все четыре, конструкция превратится в механизм – брус АВ упадёт. Поэтому степень статической неопределённости этой системы равна трём. Для системы, показанной на рис.2.9, степень статической неопределимости равна единице. Степень статической неопределимости ничем не ограничена.

Рис.2.10

Недостающие для определения усилий уравнения могут быть получены из рассмотрения деформации системы.

Статически неопределимые конструкции, элементы которых работают на растяжение и сжатие, будем рассчитывать, придерживаясь следующего порядка.

1. Статическая сторона задачи. Составляем уравнения равновесия отсечённых элементов конструкций, содержащие неизвестные усилия.

2. Геометрическая сторона задачи. Рассматривая систему в деформированном состоянии, устанавливаем связи между деформациями или перемещениями отдельных элементов конструкции. Полученные уравнения называются уравнениями совместности деформаций.

3. Физическая сторона задачи. На основании закона Гука выражаем деформации элементов конструкций через действующие в них неизвестные усилия. В случае изменения температуры к деформациям, вызванным усилиями, добавляются температурные деформации.

4. Синтез. Решая совместно статические и геометрические уравнения, выраженные через физические, находим неизвестные усилия.

5. Расчёт на прочность. Из условия прочности стержней, в зависимости от поставленной задачи, находим площади поперечного сечения стержней или действующие напряжения для проверки прочности, или грузоподъёмность конструкции.

Рассмотрим примеры расчёта простых статически неопределимых конструкций.

2.5.1. Расчёт на действие нагрузки

Подобрать площади поперечного сечения стержней трёхстержневой фермы, изображённой на рис.2.11,а.

а б

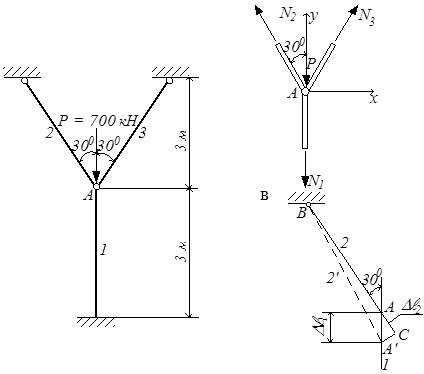
Рис.2.11

Поскольку при расчёте статически неопределимых конструкций используются уравнения совместности деформаций, выражаемые по закону Гука через жёсткость EF, а значения F нам неизвестны, необходимо заранее задавать соотношение площадей рассчитываемых стержней. Исходные данные – в табл.2.1.

Таблица 2.1.

Стержень	Площадь поперечного сечения F	Модуль Юнга E, кН/см^2	Допускаемое напряжение [σ], кН/см^2
	F1	10^4
	2F1	2·10^4

Определим длины стержней:

ℓ₁ = 3 м, ℓ₂ = ℓ₃ = 3/cos 30⁰ = 3/0,866 = 3,46 м ® ℓ₂ = 3,46 м.

Решаем задачу в соответствии с записанным выше порядком расчёта.

1. Условия равновесия узла А (рис.2.11,б) выражаются двумя уравнениями статики:

∑ х = 0: N₃sin 30⁰ – N₂sin 30⁰ = 0 ® N₃ = N₂,

∑ у = 0: N₁ + P – N₂cos 30⁰ – N₃cos 30⁰ = 0.

В результате остается одно второе уравнение, содержащее два неизвестных усилия:

N₁ + P – 2N₂cos 30⁰ = 0. (a)

Таким образом, конструкция один раз статически неопределима.

2. Так как система симметрична относительно оси среднего стержня и боковые стержни растягиваются одинаковыми силами, то узел A опустится по вертикали на величину деформации первого стержня ∆ℓ₁ и займёт положение A′ (рис.2.11,в). Стержни 2 и 3 удлиняются, на рисунке показан только второй стержень ВА и его новое положение ВА′. Удлинение бокового стержня получим, если из точки В радиусом, равным ВА′, проведём дугу и сделаем засечку на старом положении стержня ВА. Вследствие малости упругих удлинений по сравнению с длинами стержней можно дугу заменить перпендикуляром А′С, опущенным на линию АВ: АС = ∆ℓ₂. При построении картины деформированного состояния пользуемся принципом «Стержень растянулся (или сжался) и повернулся». В данном случае стержень 2 растянулся, точка A перешла в точку C, и повернулся, точка C перешла в точку A₁. Из рисунка:

∆ℓ₂ = ∆ℓ₁cos 30⁰. (б)

Уравнение (б) есть уравнение совместности деформаций.

3. Удлинения стержней выразим по закону Гука через действующие в них усилия:

.

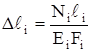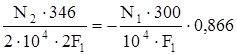® 86,5 N₂ = – 259,8 N₁ ® N₁ = – 0,33N₂. (в)

Деформация 1-го стержня записана со знаком ''–'' т.к. она – укорочение.

4. Необходимо решить совместно уравнение статики (а) и уравнение совместности деформаций, выраженное через усилия (в):

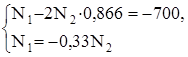
В результате решения системы уравнений получим:

N₁ = – 112,1 кН, N₂ = 339,5 кН.

5. Найдём площади поперечного сечения стержней из условия прочности :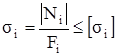

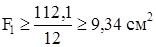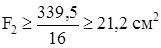, . (г)

Так как кроме условий (г) должно еще выполняться первоначально заданное соотношение F₂ = 2F₁, окончательно принимаем: F₁ = 10,6 см², F₂ = 21,2 см². При этом напряжение во втором стержне будет равно допускаемому, а в первом оно будет меньше допускаемого

.

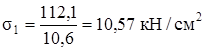Отметим, что в статически неопределимых конструкциях невозможно получить равнопрочность всех элементов – всегда есть недогруженные стержни.

2.5.2. Температурные напряжения

В элементах статически неопределимых конструкций при изменении температуры возникают усилия (напряжения). Статически определимые конструкции при изменении температуры деформируются свободно: если нагреть стержень на ∆Т градусов, то он удлинится (рис.2.12) на величину ∆ℓ_Т.

Рис.2.12

∆ℓ_Т = α ∙ ∆Т ∙ ℓ, (2.19)

где α – коэффициент линейного расширения, размерность – 1/ град.

Превратим стержень, показанный на рис.2.12, в статический неопределимый. Для этого справа установим жёсткую опору (рис.2.13).

Рис.2.13

Теперь при нагревании жёсткие опоры препятствуют удлинению стержня, в результате чего возникают реакции, направленные вдоль оси. Уравнение статики:

∑ х = 0: R_B – R_A = 0 ® R_B = R_A = R.

Уравнение совместности деформаций:

∆ℓ = ∆ℓ_Т + ∆ℓ_N = 0.

Записываем физическое уравнение, помня о том, что обе составляющие имеют знак “ + “, т.к. продольная сила N = R – растягивающая и от нагревания стержень должен удлиняться:

.

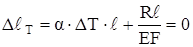Получаем формулу для напряжения в стержне при равномерном по длине нагреве

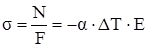. (2.20)

Теперь вернёмся к ферме, показанной на рис.2.11, и определим напряжения, возникающие в её стержнях, при равномерном нагреве одного из них. Внешняя сила Р при этом отсутствует. Исходные данные – в табл.2.2. Узел А – на рис.2.11,б, Р = 0.

Таблица 2.2.

Стержень	Площадь поперечного сечения F, см^2	Коэффициент линейного расширения α, 1/град	Изменение температуры ∆Т^0,С
	10,6	225·10^-7	+40
	21,2
1.	∑ х = 0: N3sin 30^0 – N2sin 30^0 = 0 ® N3 = N2, ∑ у = 0: N1 – 2N2cos 30^0 = 0.	(а)

2. Схема деформации – на рис.2.11,в, уравнение совместности деформации остается то же самое

∆ℓ₂ = ∆ℓ₁ ∙ cos 30⁰. (б)

3. Физическая сторона задачи:

,

.

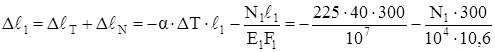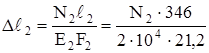В первом уравнении поставим знаки “–“, т.к. на схеме деформации системы первый стержень укорачивается. Теперь выражения для ∆ℓ подставляем в уравнение совместности деформаций (б):

.

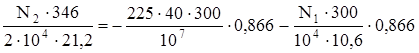Получили 8,16N₂ + 24,5N₁ = – 2338,2. (в)

4. Синтез. Решаем систему уравнений (а) и (в):

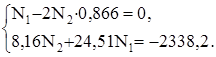
Получаем N₁ = – 80 кН, N₂ = – 46,26 кН.

5. Расчёт на прочность:

, .

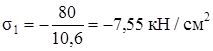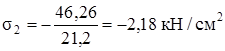Напряжения меньше допускаемых (см. табл.2.1), прочность обеспечена.

2.5.3. Монтажные напряжения

Свободная сборка статически неопределимых конструкций возможна при точном изготовлении их элементов. При отклонении размеров элементов от номинальных сборку можно осуществить с приложением усилий, вызывающих деформации элементов, поэтому в них после монтажа системы будут напряжения, называемые начальными или монтажными. В статически определимых конструкциях неточность размеров элементов не требует применения усилий при монтаже, и в элементах не возникают начальные напряжения.

Снова рассмотрим трёхстержневую статически неопределимую ферму и определим монтажные напряжения при условии, что длина первого стержня оказалась короче номинальной на величину δ (рис.2.14 и табл.2.3).

а б

Рис.2.14

Таблица 2.3

Стержень	Площадь поперечного сечения F, см^2	Модуль Юнга E, кН/см^2	Неточность изготовления δ, см
	10,6	10^4	-0,3
	21,2	2·10^4

Если величина δ незначительна по сравнению с длинами стержней, то приложив определенные усилия, можно все три стержня соединить в узле, который займёт положение А′ (рис.2.14,б). Очевидно, при этом все стержни будут растянуты, поэтому схема сил на рис. 2.11, б (Р = 0).

1. Статическая сторона этой задачи совпадает со статической стороной задачи о температурных напряжениях. Уравнения статики те же самые:

∑х = 0: N3sin 30 – N2sin30 = 0, N3= N2, ∑y = 0: N1 – 2N2cos30 = 0.

(а)

2. Геометрическая сторона задачи. Из приведённой на рис.2.14,б схемы деформации следует уравнение совместности деформаций

∆ℓ₂ = (δ – ∆ℓ₁) ∙ cos 30. (б)

3. Физическая сторона задачи. По закону Гука

,

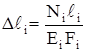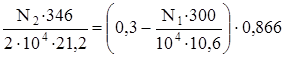Þ 8,16 N₂ = 2598 – 24,51 N₁. (в)

Следует отметить, что при записи уравнения совместности деформаций величину δ необходимо подставлять со знаком “+ “, т.к. знак “ - “ в таблице исходных данных – это лишь условное обозначение того обстоятельства, что длина стержня короче номинальной. В схеме деформации на рис.2.14,б и соответственно в уравнении совместности деформаций (б) это обстоятельство учтено.

4. Синтез. Решаем систему уравнений (а) и (б):

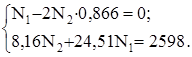
Получаем N₁ = 88,81 кН, N₂ = 51,33 кН.

5. Расчёт на прочность

, .

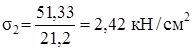Напряжения меньше допускаемых (см. табл.2.1), прочность обеспечена.

На основании рассмотренных примеров можно отметить следующие особенности статически неопределимых конструкций, которыми они отличаются от статически определимых:

1. Распределение усилий между элементами статически неопределимых конструкций зависит от жёсткостей этих элементов. Если увеличить жёсткость какого- либо из них, то он примет на себя большее усилие.

2. В статически неопределимых конструкциях при изменении температуры её элементов по сравнению с температурой, при которой осуществлялась сборка конструкций, возникают усилия и напряжения.

3. В элементах статически неопределимых конструкций могут существовать усилия и напряжения при отсутствии внешней нагрузки. Эти усилия и напряжения, называемые начальными (монтажными), появляются при сборке конструкции. Начальные напряжения или создаются с определённой целью (например, затяжка болтов, прессовая посадка, предварительно напряжённый железобетон), или возникают вследствие неточного изготовления отдельных элементов конструкций.

4. В статически неопределимых конструкциях во всех элементах одновременно нельзя получить напряжения, равные допускаемым.

2.6. Механические характеристики материалов

Для оценки прочностной надёжности конструкций необходимо изучить поведение материала в служебных условиях. В соответствии с принятой моделью материала (моделью сплошной среды) мы отказываемся от изучения внутренней микроструктуры материала (поведения кристаллической решетки, развития дислокаций и т.д.) и будем использовать феноменологический (описательный) подход. Такой подход означает, что, не вдаваясь в сущность внутренних процессов, явление (феномен) изучается по его внешним проявлениям. Феноменологический подход определяет необходимость экспериментального изучения механических свойств материалов.

Испытание материалов – это обширная специальная отрасль техники, использующая широкий спектр машин и приборов. Ограничимся лишь кратким описанием некоторых наиболее распространённых видов механи­ческих испытаний.

Испытание, как правило, заключается в изучении поведения образца в процессе деформирования его возрастающей нагрузкой до момента разру­шения. Материалы при этом ведут себя по-разному: одни к моменту разру­шения образца претерпевают значительные деформации, не исчезающие и после разрушения – это пластичные материалы (малоугле­родистая сталь, медь, латунь, алюминиевые и титановые сплавы), другие к моменту разрушения претерпевают весьма малые деформации – это хрупкие материалы (стекло, чугун, инструментальная сталь, неко­торые пластмассы).

2.6.1. Испытание на растяжение малоуглеродистой (мягкой) стали

Основной вид испытания металлов, дающий наиболее полную информацию о механических свойствах, испытание на растяжение. Для него необходимо изготовить стандартные образцы, чаще всего их делают цилиндрическими (рис.2.15). В цилиндрических образцах должно быть выдержано соотношение между расчётной длиной образца ℓ₀ и диаметром d₀: у длинных образцов ℓ₀ = 10d₀ (рис.2.15,а), у коротких ℓ₀ = 5d₀ (рис.2.15,б).

а б

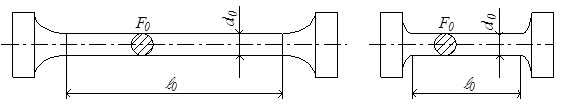
Рис. 2.15

Для испытаний на растяжение применяют разрывные машины, позволяющие в процессе испытания записать диаграмму в координатах “нагрузка – абсолютное удлинение”. Характер диаграммы растяжения зависит от свойств испытуемого материала и от скорости деформирования. Типичный вид такой диаграммы для малоуглеродистой стали при статическом приложении нагрузки изображен на рис. 2.16.

Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца:

ОА – справедлив закон Гука;

АВ – появились остаточные (пластические) деформации;

ВС – пластические деформации растут;

СД – площадка текучести (рост деформации происходит при постоянной нагрузке);

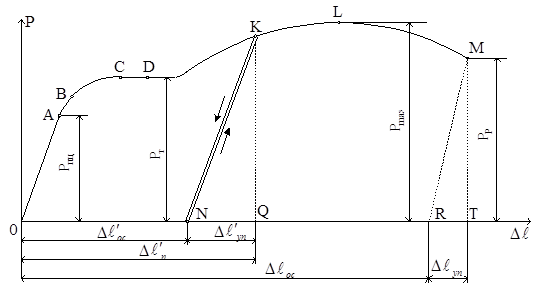
Рис.2.16

ДК – участок упрочнения (материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации и воспринимает возрастающее до некоторого предела усилие);

Точка K – испытание остановили и произвели разгрузку образца;

KN – линия разгрузки;

NKL – линия повторного нагружения образца (KL – участок упрочнения);

LM – участок падения нагрузки, в этот момент на образце появляется так называемая шейка - местное сужение;

Точка M – разрыв образца;

После разрыва образец имеет вид, примерно показанный на рис.2.17. Обломки можно сложить и измерить длину после испытания ℓ₁, а также диаметр шейки d₁.

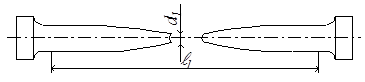
Рис.2.17

В результате обработки диаграммы растяжения и измерений образца получаем ряд механических характеристик, которые можно разделить на две группы – характеристики прочности и характеристики пластичности.

Дата добавления: 2014-01-05