Диаграммы напряжений

Разгрузка и повторное нагружение

При описании диаграммы растяжения было указано, что в точке К испыта­ние остановили и произвели разгрузку образца. Процесс разгрузки описы­вался прямой KN (рис.2.16), параллельной прямолинейному участку OA диаграммы. Это означает, что удлинение образца ∆ℓ′_П, полученное до на­чала разгрузки, полностью не исчезает. Исчезнувшая часть удлинения на диаграмме изображается отрезком NQ, оставшаяся – отрезком ОN. Следовательно, полное удлинение образца за пределом упругости состоит из двух частей – упругой и остаточной (пластической):

∆ℓ′_П = ∆ℓ′_уп + ∆ℓ′_ос.

Так будет вплоть до разрыва образца. После разрыва упругая составляющая полного удлинения (отрезок ∆ℓ_уп) исчезает. Остаточное удлинение изображается отрезком ∆ℓ_ос. Если же прекратить нагружение и разгрузить образец в пределах участка OB, то процесс разгрузки изобразится линией, совпадающей с линией нагрузки – деформация чисто упругая.

При повторном нагружении образца длиною ℓ₀ + ∆ℓ′_ос линия нагружения практически совпадает с линией разгрузки NK. Предел пропорциональности повысился и стал равным тому напряжению, от которого производилась разгрузка. Далее прямая NK перешла в кривую KL без площадки текучести. Часть диаграммы, расположенная левее линии NK, оказалась отрезанной, т.е. начало координат переместилось в точку N. Таким образом, в результате вытяжки за предел текучести, образец изменил свои механические свойства:

1). повысился предел пропорциональности;

2). исчезла площадка текучести;

3). уменьшилось относительное удлинение после разрыва.

Такое изменение свойств называется наклёпом.

При наклёпе повышаются упругие свойства и понижается пластичность. В некоторых случаях (например, при механической обработке) явление наклёпа нежелательно и его устраняют термообработкой. В других случаях его создают искусственно для улучшения упругости деталей или конструкций (обработка дробью рессор или вытяжка тросов грузоподъёмных машин).

Чтобы получить диаграмму, характеризующую механические свойства материала, первичную диаграмму растяжения в координатах Р – ∆ℓ перестраивают в координатах σ – ε. Так как ординаты σ = Р/F и абсциссы ε = ∆ℓ/ℓ получают делением на постоянные, диаграмма имеет такой же вид, как и первоначальная (рис. 2.18,а).

а б

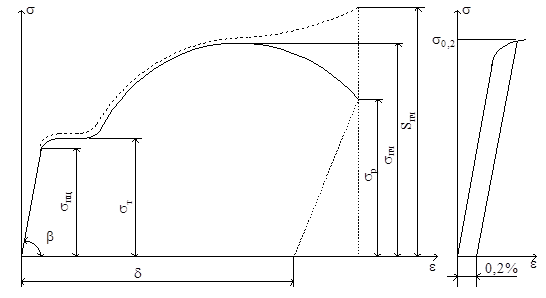
Рис.2.18

Из диаграммы σ – ε видно, что

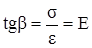, (2.28)

т.е. модуль нормальной упругости равен тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс.

По диаграмме напряжений удобно определять так называемый условный предел текучести. Дело в том, что большинство конструкционных материалов не имеет площадки текучести – прямая линия плавно переходит в кривую. В этом случае за величину предела текучести (условного) принимается напряжение, при котором относительное остаточное удлинение равно 0,2%. На рис. 2.18,б показано, как определяется величина условного предела текучести σ_0,2. Предел текучести σ_т, определяемый при наличии площадки текучести, часто называют физическим.

Нисходящий участок диаграммы носит условный характер, поскольку действительная площадь поперечного сечения образца после образования шейки значительно меньше первоначальной площади, по которой определяются координаты диаграммы. Можно получить истинное напряжение, если величину силы в каждый момент времени P_t делить на действительную площадь поперечного сечения в этот же момент времени F_t:

. (2.29)

На рис. 2.18,а, этим напряжениям соответствует штриховая линия. До предела прочности S и σ практически совпадают. В момент разрыва истинное напряжение значительно превышает и предел прочности σ_пч и тем более напряжение в момент разрыва σ_р. Выразим площадь шейки F₁ через ψ и найдем S_р.

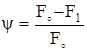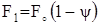Þ Þ .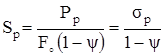

Для пластичной стали ψ = 50 – 65%. Если принять ψ = 50% = 0,5, то получим S_р = 2σ_р, т.е. истинное напряжение наибольшее в момент разрыва, что вполне логично.

2.6.2. Испытание на сжатие различных материалов

Испытание на сжатие дает меньше информации о свойствах материала, чем испытание на растяжение. Тем не менее, оно совершенно необходимо для характеристики механических свойств материала. Осуществляется на образцах в виде цилиндров, высота которых не более 1,5 диаметра, или на образцах в виде кубиков.

Рассмотрим диаграммы сжатия стали и чугуна. Для наглядности изобразим их на одном рисунке с диаграммами растяжения этих материалов (рис.2.19). В первой четверти – диаграммы растяжения, а в третьей – сжатия.

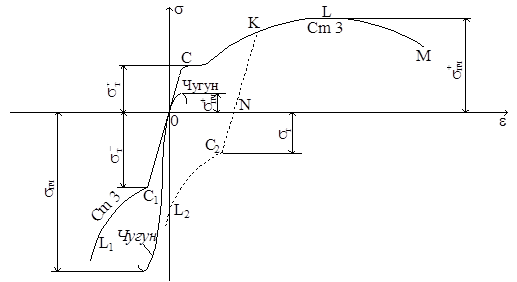
Рис.2.19

В начале загружения диаграмма сжатия стали – наклонная прямая с таким же наклоном, как и при растяжении. Потом диаграмма переходит в участок текучести (площадка текучести выражена не так отчетливо, как при растяжении). Далее кривая слегка изгибается и не обрывается, т.к. стальной образец не разрушается, а только сплющивается. Модуль упругости стали Е при сжатии и растяжении одинаков. Также одинаковы и предел текучести σ_т⁺ = σ_т^-. Предел прочности при сжатии получить невозможно, как и невозможно получить характеристики пластичности.

Диаграммы растяжения и сжатия чугуна по форме похожи: искривляются с самого начала и по достижении максимальной нагрузки обрываются. Однако на сжатие чугун работает лучше, чем на растяжение (σ_пч^- = 5 σ_пч⁺). Предел прочности σ_пч – это единственная механическая характеристика чугуна, получаемая при испытании на сжатие.

Трение, возникающее во время испытания между плитами машины и торцами образца, оказывает существенное влияние на результаты испытания и на характер разрушения. Цилиндрический стальной образец принимает бочкообразную форму (рис. 2.20,а), в чугунном кубике возникают трещины под углом 45⁰ к направлению нагрузки. Если исключить влияние трения, смазав торцы образца парафином, трещины возникнут по направлению нагрузки и наибольшая сила будет меньше (рис.2.20,б и в). Большинство хрупких материалов (бетон, камень) разрушается при сжатии так же, как чугун, и имеет аналогичную диаграмму сжатия.

а б в г д

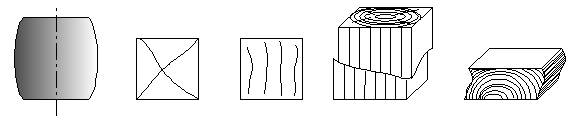
Рис.2.20

Представляет интерес испытание древесины – анизотропного, т.е. обладающего различной прочностью в зависимости от направления силы по отношению к направлению волокон, материала. Анизотропными являются и все более широко применяемые стеклопластики. При сжатии вдоль волокон древесина значительно прочнее, чем при сжатии поперек волокон (кривые 1 и 2 на рис.2.21). Кривая 1 похожа на кривые сжатия хрупких материалов. Разрушение происходит вследствие сдвига одной части кубика относительно другой (рис.2.20,г). При сжатии поперек волокон древесина не разрушается, а прессуется (рис. 2.20,д).

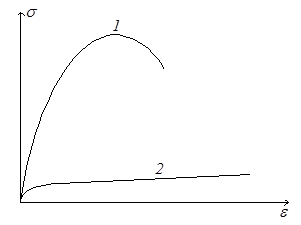
Рис.2.21

При испытании на растяжение стального образца мы обнаружили изменение механических свойств в результате вытяжки до появления заметных остаточных деформаций – наклёп. Посмотрим, как ведет себя образец после наклёпа при испытании на сжатие. На рис.2.19 диаграмма показана пунктиром. Сжатие идет по кривой NC₂L₂, которая располагается выше диаграммы сжатия образца, не подвергавшегося наклёпу OC₁L₁, и почти параллельно последней. После наклёпа растяжением пределы пропорциональности и текучести при сжатии уменьшаются. Это явление называется эффектом Баушингера по имени учёного, впервые его описавшего.

2.6.3. Определение твёрдости

Очень распространённым механико-технологическим испытанием является определение твёрдости. Это обусловлено быстротой и простотой таких испытаний и ценностью получаемой информации: твёрдость характеризует состояние поверхности детали до и после технологической обработки (закалки, азотирования и т.п.), по ней можно косвенно судить о величине предела прочности.

Твёрдостью материала называется способность оказывать сопротивление механическому проникновению в него другого, более твёрдого тела. Величины, характеризующие твёрдость, называют числами твёрдости. Определяемые разными методами, они различны по величине и по размерности и всегда сопровождаются указанием способа их определения.

Наиболее распространённый метод – по Бринеллю. Испытание заключается в том, что в образец вдавливают стальной закалённый шарик диаметра D (рис.2.22,а). Шарик выдерживается некоторое время под нагрузкой P, в результате чего на поверхности остается отпечаток (лунка) диаметром d. Отношение нагрузки в кН к площади поверхности отпечатка в см² называется числом твёрдости по Бринелю

. (2.30)

Для определения числа твёрдости по Бринелю используют специальные испытательные приборы, диаметр отпечатка измеряется портативным микроскопом. Обычно HB не считают по формуле (2.30), а находят из таблиц.

а б

Рис.2.22

Пользуясь числом твёрдости HB, можно без разрушения образца получить приближённое значение предела прочности некоторых металлов, т.к. существует линейная связь между σ_пч и HB: σ_пч = k ∙ HB (для малоуглеродистой стали k = 0,36, для высокопрочной стали k = 0,33, для чугуна k = 0,15, для алюминиевых сплавов k = 0,38, для титановых сплавов k = 0,3).

Весьма удобен и широко распространён метод определения твердости по Роквеллу. В этом способе в качестве индентора, вдавливаемого в образец, используется алмазный конус с углом при вершине 120 градусов и радиусом закругления 0,2 мм, или стальной шарик диаметром 1,5875 мм (1/16 дюйма). Испытание происходит по схеме, приведённой на рис. 2.22,б. Сначала конус вдавливается предварительной нагрузкой P₀ = 100 H, которая не снимается до конца испытания. При этой нагрузке конус погружается на глубину h₀. Затем на конус подается полная нагрузка P = P₀ + P₁ (два варианта: A – P₁ = 500 H и C – P₁ = 1400 H), при этом глубина вдавливания увеличивается. После снятия основной нагрузки P₁ остается глубина h₁. Глубина отпечатка, полученная за счёт основной нагрузки P₁, равная h = h₁ – h₀, характеризует твердость по Роквеллу. Число твёрдости определяется по формуле

, (2.31)

где 0,002 – цена деления шкалы индикатора твердомера.

Существуют и другие методы определения твёрдости (по Виккерсу, по Шору, микротвёрдость), которые здесь не рассматриваются.

2.6.4. Сравнение свойств различных материалов

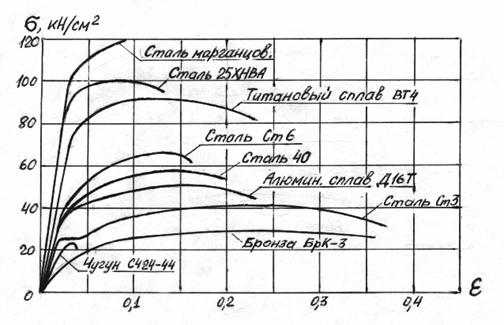Мы уже подробно рассмотрели свойства пластичного и хрупкого материалов – малоуглеродистой стали и серого чугуна - при растяжении и сжатии. Продолжим это сравнение – рассмотрим диаграммы растяжения некоторых металлов (рис.2.23).

Рис.2.23

Все показанные на рисунке стали –40, Ст6, 25ХНВА, марганцовистая – имеют гораздо более высокие характеристики прочности, чем малоуглеродистая сталь Ст3. Площадка текучести у высокопрочных сталей отсутствует, относительное удлинение при разрыве δ значительно меньше. За повышение прочности приходится платить понижением пластичности. Хорошей пластичностью обладают алюминиевый и титановый сплавы. При этом прочность алюминиевого сплава выше, чем у Ст3, а удельный вес почти в три раза меньше. А титановый сплав имеет прочность на уровне высокопрочной легированной стали при почти в два раза меньшем удельным весе. В табл.2.4 приведены механические характеристики некоторых современных материалов.

Таблица 2.4

Материал	Марка	Предел текучести, σт	Предел прочности, σпч	Относит. удлинение при разрыве, δ5	Относит сужение при разрыве, ψ	Удельный вес, γ	Модуль Юнга, E
		кН/см^2	кН/см^2	%	%	Н/см^3	кН/см^2
Сталь углеродистая горячекатаная	Ст3		34-42			0,0785	2·10^4
Сталь углеродистая горячекатаная	СТ6		60-72			0,0785	2·10^4
Сталь углеродистая качественная						0,0785	2·10^4
Сталь легированная хромникельвольфрамовая	25ХНВА					0,082	2,1·10^4
Сталь легированная кремнехроммарганцовистая	35ХГСА					0,09	2,1·10^4
Чугун	СЧ24-44	-		-	-	0,072	1,5·10^4
Алюминиевый сплав	Д16Т				-	0,028	0,7·10^4
Бронза кремнистая	БрК-3	-			-	0,085	1,1·10^4
Титановый сплав	ВТ4				-	0,045
Стеклопластик	СВАМ	-			-	0,019	0,4·10^4
Углепластик	КЕВЛАР			-	-	0,017	3·10^4

В последних двух строчках таблицы приведены характеристики полимерных композиционных материалов, отличающихся малым весом и высокой прочностью. Особо выдающимися свойствами отличаются композиты на основе суперпрочных углеродных волокон – прочность их примерно в два раза выше прочности самой лучшей легированной стали и на порядок – малоуглеродистой стали. Они жестче стали в полтора раза и легче почти в пять раз. Применяются, конечно, в военной технике – авиа- и ракетостроении. В последние годы начинают применяться и в гражданских областях – автомобилестроении (кузова, тормозные диски, выхлопные трубы гоночных и дорогих спортивных машин), судостроении (корпуса катеров и малых судов), медицине (инвалидные коляски, детали протезов), машиностроении для спорта (рамы и колеса гоночных велосипедов и другой спортивный инвентарь). Широкому применению этого материала пока препятствует его высокая стоимость и низкая технологичность.

Резюмируя все вышесказанное о механических свойствах различных материалов, можно сформулировать основные особенности свойств пластичных и хрупких материалов.

1. Хрупкие материалы, в отличие от пластичных, разрушаются при незначительных остаточных деформациях.

2. Пластичные материалы одинаково сопротивляются растяжению и сжатию, хрупкие – хорошо сжатию и плохо растяжению.

3. Пластичные материалы хорошо сопротивляются ударным нагрузкам, хрупкие – плохо.

4. Хрупкие материалы очень чувствительные к так называемой концентрациинапряжений (локальным всплескам напряжений вблизи мест резкого изменения формы деталей). На прочность деталей из пластичного материала концентрация напряжений влияет в гораздо меньшей степени. Более подробно об этом – чуть ниже.

5. Хрупкие материалы не поддаются технологической обработке, связанной с пластической деформацией – штамповке, ковке, волочению и т.п.

Деление материалов на пластичные и хрупкие носит условный характер, так как при некоторых условиях хрупкие материалы получают пластические свойства (например, при большом всестороннем сжатии) и, наоборот, пластичные материалы приобретают хрупкие свойства (например, мягкая сталь при низкой температуре). Поэтому правильнее говорить не о пластичном и хрупком материалах, а об их пластическом и хрупком разрушении.

2.7. Допускаемые напряжения

Как уже указывалось, детали машин и других конструкций должны удовлетворять условиям прочности (2.3) и жёсткости (2.13). Величина допускаемых напряжений устанавливается в зависимости от материала (его механических характеристик), вида деформации, характера действия нагрузок, условий работы конструкций и тяжести последствий, которые могут наступить в случае разрушения:

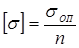, (2.32)

где σ_ОП – напряжение, соответствующее наступлению опасного состояния для данного материала; n – коэффициент запаса прочности, n > 1.

Для деталей, выполненных из пластичного материала, опасное состояние характеризуется появлением больших остаточных деформаций, поэтому опасное напряжение равно пределу текучести σ_оп = σ_т.

Для деталей, изготовленных из хрупкого материала, опасное состояние характеризуется появлением трещин, поэтому опасное напряжение равно пределу прочности σ_оп = σ_пч.

Все перечисленные выше условия работы деталей учитываются коэффициентом запаса прочности. При любых условиях имеют место некоторые общие факторы, учитываемые коэффициентом запаса прочности:

1. Неоднородность материала, следовательно, разброс механических характеристик;

2. Неточность задания величин и характера внешних нагрузок;

3. Приближённость расчётных схем и методов расчёта.

На основании данных длительной практики конструирования, расчёта и эксплуатации машин и сооружений величина коэффициента запаса прочности для стали принимается равной 1,4 – 1,6. Для хрупких материалов при статической нагрузке принимают запас прочности 2,5 – 3,0. Итак, для пластичных материалов:

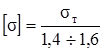. (2.33)

Для хрупких материалов

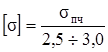. (2.34)

При сравнении свойств пластичных и хрупких материалов отмечалось, что на прочность влияет концентрация напряжений. Теоретические и экспериментальные исследования показали, что равномерное распределение напряжений по площади поперечного сечения растянутого (сжатого) стержня в соответствии с формулой (2.2) нарушается вблизи мест резкого изменения формы и размера поперечного сечения – отверстий, галтелей, выкружек и др. Около этих мест возникают локальные всплески напряжений – концентрация напряжений.

Для примера рассмотрим концентрацию напряжений в растягиваемой полосе с малым отверстием. Отверстие считается малым, если выполняется условие d ≤ b/5 (рис.2.27,а). При наличии концентрации напряжение определяется по формуле:

σ_max = α_σ∙ σ_nom. (2.35)

где α_σ – коэффициент концентраций напряжений, определяемый методами теории упругости или экспериментально на моделях;

σ_nom – номинальное напряжение, т.е. напряжение, вычисленное для данной детали при отсутствии концентрации напряжений.

Для рассматриваемого случая (α_σ = 3 и σ_nom = N/F) эта задача является в известном смысле классической задачей о концентрации напряжений и называется по имени решившего её в конце XIX века учёного задачей Кирша.

Рассмотрим, как поведет себя полоса с отверстием по мере увеличения нагрузки. В пластичном материале максимальное напряжение у отверстия станет равным пределу текучести (рис.2.27,б). Концентрация напряжений всегда очень быстро затухает, поэтому уже на небольшом удалении от отверстия напряжение гораздо меньше. Увеличим нагрузку (рис.2.27,в): напряжение у отверстия не увеличивается, т.к. пластичный материал имеет довольно протяжённую площадку текучести, уже на некотором удалении от отверстия напряжение становится равным пределу текучести.

а б в г

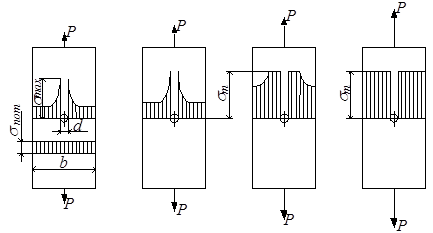
Рис.2.27

Дальнейшее увеличение нагрузки (рис.2.27,г) приводит к распространению текучести на все ослабленное сечение – наступает опасное (предельное) состояние. Причем, это предельное состояние совершенно не отличается от такового для полосы без отверстия. Вывод – пластичный материал (мягкая малоуглеродистая сталь) не чувствителен к концентрации напряжений при статической нагрузке.

В хрупком материале распределение напряжений в начале нагружения не отличается от такового в пластичном материале (рис.2.27,а). Нагрузка растёт до тех пор, пока напряжение на границе отверстия не станет равным пределу прочности. И хотя на небольшом удалении от отверстия напряжение гораздо меньше, это состояние является опасным (предельным), т.к. на поверхности отверстия появились трещины. Эти трещины растут очень быстро при постоянной нагрузке и наступает момент разрушения полосы. Вывод – хрупкий материал очень чувствителен к концентрации напряжений. Поэтому коэффициент запаса прочности принимается равным n = 3,0 – 9,0.

При циклических и динамических напряжениях пластичные стали чувствительны к концентрации напряжений. Ориентировочные величины основных допускаемых напряжений на растяжение и сжатие при статической нагрузке приведены в табл.2.5.

Таблица 2.5

Материал	Допускаемое напряжение, МПа
растяжение	сжатие
Сталь Ст3
Сталь машиностроительная углеродистая	160-250
Сталь машиностроительная легированная	200-400 и выше
Чугун серый в отливках	28-80	120-150
Латунь	70-140
Алюминиевый сплав	80-150
Сосна вдоль волокон	7-10	10-12
Кирпичная кладка	до 0,2	0,6-2,5
Бетон	0,1-0,7	1-9

2.8. Потенциальная энергия упругой деформации

Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругой деформации. При этом точка приложения внешней силы перемещается, потенциальная энергия положения груза убывает на величину, которая численно равна работе, совершённой внешней силой. Таким образом, потенциальная энергия упругой деформации U равна работе внешней силы А. Найдём величину А (рис.2.28).

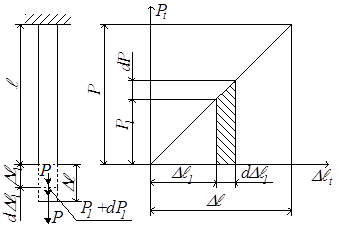
Рис.2.28

Внешняя сила P_t растёт от нуля до конечного значения Р. Соответственно и деформация ∆ℓ_t растёт от нуля до конечного значения ∆ℓ. Пусть некоторой растягивающей силе P₁ соответствует деформация ∆ℓ₁. Дадим силе бесконечно малое приращение dP₁, при этом деформация получит приращение d∆ℓ₁. Очевидно, работа внешней силы на этом перемещении

dA = (P₁ + dP₁)d∆ℓ₁ ≈ P₁∙ d∆ℓ₁,

dA равна площади заштрихованной фигуры.

,

.

Теперь найдём работу внешней силы:

.

Итак, потенциальная энергия упругой деформации

. (2.36)

Если поделить U на объём образца Fℓ, получим удельную потенциальную энергию упругой деформации

. (2.37)

Потенциальная энергия деформации накапливается в обратимой форме – в процессе разгрузки тела она освобождается, превращаясь снова в энергию внешних сил и совершая работу. Таким образом, упругое тело – это аккумулятор энергии.

Глава 3. НАПРЯЖЁННОЕ И ДЕФОРМИРОВАННОЕ

СОСТОЯНИЕ В ТОЧКЕ. ТЕОРИИ ПРОЧНОСТИ

3.1. Компоненты напряжений. Виды напряжённых состояний

Центральное растяжение или сжатие бруса является самым простым видом деформации тела, когда напряжение во всех его точках одинаково (однородное напряжённое состояние). В произвольным образом нагруженном теле (рис.3.1,а) напряжение меняется от точки к точке и поэтому в произвольном сечении m-n этого тела напряжения распределены неравномерно. В этом случае при изучении распределения напряжений в окрестности произвольной точки K рассматриваемого сечения m-n мысленно вырезают бесконечно малый параллелепипед (рис.3.1,б). Ввиду его малости можно считать, что по граням напряжения распределены равномерно. На рис.3.1,в показаны напряжения, действующие по граням бесконечно малого параллелепипеда.

а б в

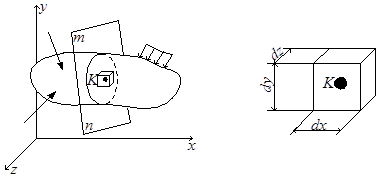
Рис.3.1

σ_х – нормальное напряжение, действующее по направлению оси x; положительное при растяжении, отрицательное при сжатии;

τ_ху – касательное напряжение, действующее по площадке с нормалью х (первый индекс) в направлении оси у (второй индекс); положительно, если стремится развернуть элемент по часовой стрелке (глядя со стороны положительного направления оси).

На рис.3.1,в нормальные напряжения σ_х, σ_у и σ_z положительные, касательные напряжения τ_ху < 0, τ_ух > 0. Под действием приложенных к нему напряжений элемент должен находиться в равновесии, следовательно, для него можно записать уравнения статики. Покажем напряжения, дающие момент относительно оси OZ (рис.3.2) и запишем соответствующее уравнение статики:

∑ M_oz = 0: ; (3.1)

τ_ух = τ_ху..

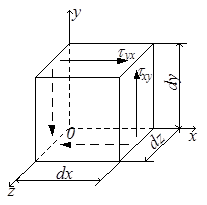
Рис.3.2

Учитывая правило знаков, перепишем формулу (3.1)

– τ_ху = τ_ух, – τ_zx = τ_xz, – τ _zy = τ_yz. (3.2)

Формула (3.2) выражает закон парности касательных напряжений: на любых взаимно перпендикулярных площадках касательные напряжения с одноимёнными индексами равны по величине и вращают элемент в противоположные стороны.

Таким образом, шесть независимых компонентов напряжений σ_х, σ_у, σ_z, τ_ху, τ_ух, τ_zx – характеризуют напряжённое состояние в точке.

Напряжённым состоянием в точке называется совокупность напряжений, действующих по всевозможным площадкам, проведённым через эту точку.

При повороте бесконечно малого параллелепипеда меняются компоненты напряжённого состояния. Всегда можно найти такое его положение, что по граням (площадкам) параллелепипеда будут действовать только нормальные напряжения. Такие площадки называются главными, а нормальные напряжения, по ним действующие, называются главными нормальными напряжениями (рис.3.3).

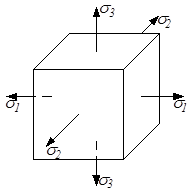
Рис.3.3

Это положение доказывается в теории упругости. Главные нормальные напряжения принято обозначать цифровыми индексами по следующему правилу: σ₁ > σ₂ > σ₃. Соблюдение этого правила важно с точки зрения расчёта на прочность. Например: три главных напряжения имеют значения 120 МПа, – 50МПа и – 30 МПа; их надо записать σ₁ = 120 МПа, σ₂ = – 30 МПа и σ₃ = – 50 МПа.

Напряжённое состояние в точке классифицируется на три вида: линейное (одноосное), плоское (двухосное) и объёмное (трёхосное) в зависимости от того, испытывает ли параллелепипед растяжение (сжатие) в одном, двух или трёх взаимно перпендикулярных направлениях (рис.3.4).

а б в

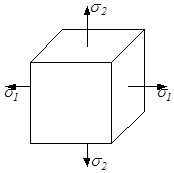
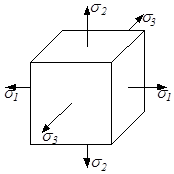
Рис.3.4

3.2. Линейное напряжённое состояние

Линейное напряжённое состояние имеет место в стержнях, испытывающих растяжение или сжатие, а также в некоторых точках стержня, работающего на изгиб. Рассмотрим растяжение стержня. Как указывалось в главе 2, в поперечных сечениях, удалённых от точек приложения внешних сил, нормальные напряжения распределены равномерно и равны (рис.3.5,а)

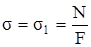. (3.3)

Эти напряжения являются главными, т.к. касательные напряжения в поперечном сечении равны нулю. Напряжённое состояние при растяжении является однородным, поэтому размеры выделяемых элементов не играют никакой роли. Определим напряжения, действующие по наклонной площадке. Наклон площадки определяется острым углом α между направлением оси стержня и нормалью n_α к площадке. Условимся считать угол α положительным, если он отсчитывается против часовой стрелки (рис.3.5,а). Элемент, находящийся в линейном напряжённом состоянии, изображаем в виде плоской фигуры, помня, однако, что в действительности он имеет вид, показанный на рис.3.4,а.

Рассмотрим равновесие нижней части стержня, отсечённой наклонной площадкой (рис.3.5,б). По наклонной площадке, площадь которой равна F_α, равномерно распределены напряжения p_α, параллельные осевой силе N = P, следовательно, результирующая этих напряжений

p_αF_α = N.

Отсюда найдём p_α, подсчитав предварительно ,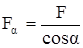

.

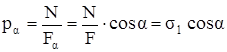Проектируя p_α на нормаль n_α и на плоскость сечения, получим выражения для нормальных и касательных напряжений по наклонной площадке:

σ_α = p_αcos α, τ_α = p_αsin α

или

σ_α = σ₁cos²α. (3.4)

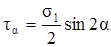. (3.5)

а б в

Рис.3.5

Как видно из формул (3.4) и (3.5), при α = 0 ® τ_α = 0 и σ_α = σ₁, при α = π/2 ® σ_α = 0 и τ_α = 0. Таким образом, при растяжении действительно имеет место линейное напряжённое состояние: σ₁ = N/F, σ₂ = σ₃ = 0. При сжатии σ₃ = – N/F, σ₁ = σ₂ = 0.

Из выражения (3.5) видно, что касательные напряжения достигают своей наибольшей величины при α = ± 45⁰, причём

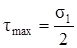. (3.6)

Определим теперь напряжения, действующие по площадке, перпендикулярной заданной наклонной, α₁ = α + 90⁰ (рис.3.5,в):

σ_α1 = σ₁ ∙ cos² (α + 90) = σ₁sin² α,

.

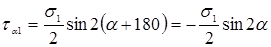Итак

σ_α+90 = σ₁sin² α. (3.7)

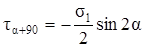. (3.8)

3.3. Плоское напряжённое состояние

Плоское напряжённое состояние встречается в деталях машин и в строительных конструкциях очень часто. Например, это стержень при кручении (рис.3.6,а) и изгибе (рис.3.6,б), тонкостенный сосуд под действием внутреннего давления (рис.3.6,в).

а б в

Рис.3.6

Плоское напряжённое состояние также имеет место в тонкой пластине, нагруженной силами, параллельными её плоскости и равномерно распределёнными по толщине (рис.3.7): σ_х ≠ 0, σ_у ≠ 0, τ_ху ≠ 0, σ_z = τ_zx = τ_zy = 0.

Рассмотрим два аспекта задачи о плоском напряжённом состоянии: найдём напряжения, действующие по наклонной площадке (прямая задача), и найдём величины и направления главных напряжений (обратная задача).

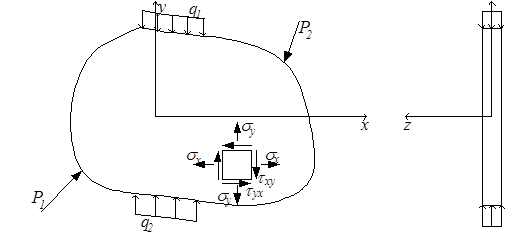
Рис.3.7

3.3.1. Прямая задача

Дано: напряжения σ_х, σ_у, τ_ху, угол α > 0 (рис.3.8,а).

Определить: напряжения σ_α и τ_α (рис.3.8,б).

Рассмотрим равновесие элемента abc. При записи уравнений статики будем определять силу как произведение напряжения на площадь соответствующей грани:

площадь наклонной грани bc = dF;

площадь прямой грани ab = dF ∙ cos α;

площадь прямой грани ac = dF ∙ sin α.

а б в

Рис.3.8

Теперь запишем уравнения проекций всех сил, действующих на элемент abc, на нормаль к наклонной площадке и на ось, совпадающую с этой площадкой (рис.3.8,в).

∑n = 0: σ_αdF – σ_x dF cos α ∙ cos α – σ_у dF sin α ∙ sin α + τ_xу dF cos α ∙ sin α + τ_ух dF sin α ∙ cos α = 0,

∑t = 0: τ_αdF + σ_у dF sin α ∙ cos α + τ_уx dF sin α ∙ sin α – τ_xу dF cos α ∙ cos α – σ_х dF cos α ∙ sin α = 0.

После несложных преобразований и сокращения на dF получаем следующие выражения:

σ_α = σ_х cos²α + σ_y sin²α – τ_xy sin 2α, (3.9)

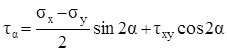. (3.10)

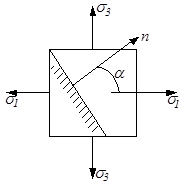Рис.3.9

Если исходные площадки являются главными (рис.3.9), то формулы (3.9) и (3.10) упрощаются: σα = σ1cos^2α + σ2sin^2, (3.11) 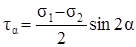. (3.12) Из формулы (3.12) следует, что наибольшее касательное напряжение

действует по площадке, наклонённой под углом 45⁰ к главным площадкам:

. (3.13)

Преобразуем формулу (3.9), используя выражение для тригонометрических функций

и .

Получим

. (3.14)

Теперь определим напряжения, действующие по площадке, перпендикулярной к заданной: α₁ = α + 90⁰. Воспользуемся формулой (3.14), учитывая, что cos 2α₁ = – cos 2α и sin 2α₁ = – sin 2α. Получим

. (3.15)

Сложим (3.14) и (3.15), чтобы найти сумму нормальных напряжений, действующих по взаимно перпендикулярным площадкам.

Получим

σ_α + σ_{α + 90} = σ_х + σ_у = const, (3.16)

т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам инвариантна по отношению к наклону этих площадок.

3.3.2. Обратная задача

Дано: напряжения σ_х, σ_у, τ_ху (рис.3.8,а).

Определить: положение главных площадок и величины главных напряжений σ₁ и σ₂.

По определению на главных площадках τ_α = 0. Из формулы (3.10) найдём угол α₀ между осью х и одним из главных напряжений.

,

. (3.17)

Величины главных напряжений можно найти по формулам (3.14) и (3.15), подставив в них α₀. Удобнее иметь формулы для главных напряжений, не зависящие от углов и тригонометрических функций. Для вывода используем зависимости косинуса и синуса двойного угла от тангенса

, .

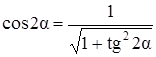Подставим их в формулу (3.14):

. (*)

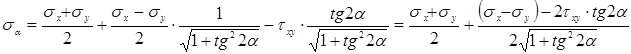Теперь в выражение (*) подставим tg 2α₀ по формуле (3.17) и получим значение большего главного напряжения

.

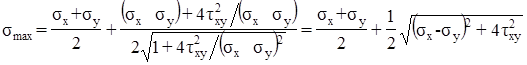Второе главное напряжение получим, используя формулу (3.15). В результате выражение для главных напряжений при плоском напряжённом состоянии имеет следующий вид:

. (3.18)

Для определения σ_max после первого слагаемого ставим «+», а для определения σ_min ставим «–». Следует обратить внимание на то, что если одно из главных напряжений, вычисленных по формуле (3.18), окажется отрицательным, то их следует обозначить σ₁ и σ₃. Если же оба главных напряжений окажутся отрицательными, то σ₂ и σ₃; оба положительными, то σ₁ и σ₂.

Главные напряжения обладают свойством экстремальности – одно из них наибольшее, другое – наименьшее из всех возможных в данной точке тела (помним о том, что сумма нормальных напряжений на взаимно перпендикулярных площадках постоянна). Для доказательства исследуем на экстремум функцию σ_α (формула 3.9). Продифференцируем её и приравняем производную нулю.

®

® – 2τ_xy cos 2α = (σ_x – σ_y)sin 2α ® .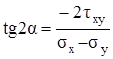

Площадки, характеризуемые этими углами, являются главными в соответствии с формулой (3.17).

3.4. Объёмное напряжённое состояние. Общие понятия

Объёмное напряжённое состояние встречается реже, чем плоское. Пример – толстостенный сосуд давления (рис.3.10). Подробным образом изучают объёмное напряжённое состояние в курсе теории упругости, в сопротивлении материалов – только основные понятия.

Рис.3.10

Рассмотрим объёмное напряжённое состояние, заданное главными напряжениями (рис.3.11).

Рис.3.11

Напряжения, действующие по наклонной площадке с нормалью n, находятся по формулам

σ_α = σ₁cos²α₁ + σ₂cos²α₂ + σ₃cos²α₃, (3.19)

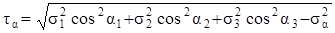. (3.20)

Эти формулы приведены без вывода. В них α₁, α₂, α₃ – углы, которые образуют нормаль к площадке n с осями x, y, z соответственно.

Если наклонная площадка параллельна одному из главных напряжений, то напряжения, по ней действующие, не зависят от этого главного напряжения. Они определяются по формулам плоского напряженного состояния в зависимости от двух других главным напряжений. Учитывая, что главные напряжения экстремальные, т.е. σ₁ = σ_max и σ₃ = σ_min, легко найти наибольшее касательное напряжение. Очевидно, оно действует по площадке, параллельной σ₂ и наклоненной под углом 45⁰ к σ₁ и σ₃ (рис.3.12). Определяется формулой (3.13)

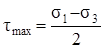. (3.21)

Рис.3.12

Известный интерес, особенно при изучении пластических деформаций, представляют напряжения, действующие по площадке, равнонаклонённой ко всем главным направлениям. Такая площадка называется октаэдрической, поскольку она параллельна грани октаэдра, который может быть образован из куба. Нормаль к этой площадке образует равные углы с главными направлениями:

α₁ = α₂ = α₃ = α.

Учитывая, что всегда

cos²α₁ + cos²α₂ + cos²α₃ = 1_,

Получаем

cos²α = ⅓.

Тогда из формул (3.19) и (3.20) находим

, (3.22)

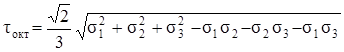. (3.23)

При изучении вопросов прочности деформация бесконечно малого элемента разделяется на деформацию изменения объёма и деформацию искажения формы. Оказывается, что σ_окт «ответственно» за изменение объёма, а τ_окт – за изменение формы.

Напряжение σ_окт представляет собой среднее напряжение для данного объемного напряженного состояния, σ_окт = σ_ср

3.5.Деформации при объёмном напряжённом состоянии.

Закон Гука

3.5.1. Обобщённый закон Гука

Исследуя деформации и рассматривая вопросы прочности при объёмном и плоском напряжённом состояниях, будем в соответствии с основными гипотезами предполагать, что материал следует закону Гука, а деформации малы.

Изучая центральное растяжение (сжатие) прямого бруса, мы выяснили, что при линейном напряжённом состоянии бесконечно малый элемент испытывает продольную и поперечную деформации, связанные с напряжением формулами (2.9) и (2.7);

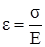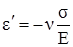, . (3.24)

Напомним, что Е – модуль нормальной упругости и ν - коэффициент Пуассона – упругие постоянные материала.

Рассмотрим деформацию элемента, находящегося в объёмном напряжённом состоянии (рис.3.13,а). Определим относительные деформации в главных направлениях ε₁, ε₂ и ε₃. Применяя принцип суперпозиции, можно записать

ε₁ = ε₁₁ + ε₁₂ + ε₁₃.

где ε₁₁ – относительное удлинение в направлении σ₁, вызванное действием только σ₁ (рис. 3.13,б);

ε₁₂ – удлинение в том же направлении, вызванное действием только σ₂ (рис. 3.13,в);

ε₁₃ – удлинение в том же направлении, вызванное действием только σ₃ (рис. 3.13,г).

Поскольку направление σ₁ для самого напряжения σ₁ является продольным, а для напряжений σ₂ и σ₃ – поперечным, то по формулам (3.24) находим

, , .

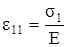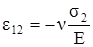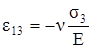Сложив эти величины, будем иметь

.

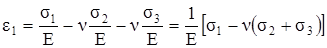а б в

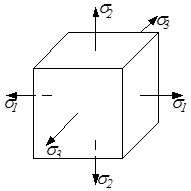
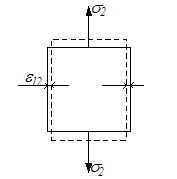
г

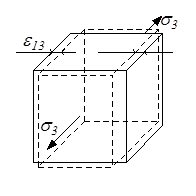
Рис.3.13

Аналогично получим выражения и для двух других главных удлинений. В результате

(3.25)

Формулы (3.25) носят название обобщённого закона Гука для изотропного тела. Заметим, что сжимающие напряжения подставляют в эти формулы со знаком минус. Из формул (3.25) легко можно получить закон Гука для плоского напряжённого состояния. Например, для случая σ₂ = 0

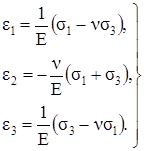(3.26)

Подчеркнём, что равенство нулю напряжения σ₂ не означает, что ε₂ также равно нулю. Например, при растяжении пластинки в её плоскости по второй формуле (3.26) можно определить уменьшение толщины пластинки.

Выражения (3.25) справедливы не только для главных деформаций, но и для относительных линейных деформаций по любым трём взаимно перпендикулярным направлениям, поскольку при малых деформациях влияние сдвига от действия касательных напряжений на линейную деформацию представляет собой величину второго порядка малости. Иными словами, индексы «1», «2» и «3» могут быть заменены на индексы х, у и z.

3.5.2. Относительная объёмная деформация

Установим связь между относительным изменением объёма элементарного параллелепипеда и главными напряжениями. До деформации размеры сторон были dx, dy и dz (рис.3.14,а). После деформации эти размеры стали dx + ∆dx, dy + ∆dy и dz + ∆dz (рис.3.14,б).

а б

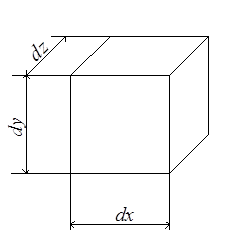
Рис.3.14

Начальный объём параллелепипеда V₀ = dx∙dy∙dz. Объём после деформации V₁ = (dx + ∆dx)(dy + ∆dy)(dz + ∆dz).

Найдём абсолютное изменение объёма параллелепипед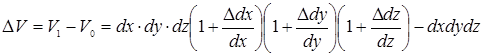а:

. (а)

В скобках выражения (а) содержатся относительные удлинения

, , .

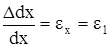Произведя в выражении (а) перемножение величин, стоящих в скобках, получим

∆V = V₀ ∙ (1 + ε₁ + ε₂ + ε₃ + ε₁ε₂ + ε₂ε₃ + ε₁ε₃ + ε₁ε₂ε₃) – V₀.

Учитывая малость относительных деформаций, произведением их можно пренебречь. Тогда относительное изменение объёма

. (3.27)

Выразив главные удлинения через главные напряжения при помощи формул обобщённого закона Гука (3.25), получим:

. (3.28)

Формулу (3.28) перепишем в несколько ином виде, с учётом (3.22)

σ₁ + σ₂ + σ₃ = 3σ_окт = 3σ_ср.

Тогда

(3.29)

или

σ_ср = K ∙ θ, (3.30)

где

. (3.31)

Величина К называется модулем объёмной деформации. Формула (3.30) представляет собой компактную, отличную от (3.25), формулу записи обобщённого закона Гука. Она удобна ещё и тем, что совпадает по структуре с законом Гука при линейном напряжённом состоянии (σ = Еε).

Из формулы (3.28) видно, что при деформации тела, материал которого имеет коэффициент Пуассона ν = 0,5 (например, резина или сталь в пластичном состоянии) объём тела не меняется. Материал ведёт себя как несжимаемая жидкость.

Из формулы (3.28) также следует, что коэффициент Пуассона не может быть больше 0,5. Действительно, при равномерном всестороннем сжатии (гидростатическом давлении) σ_ср = – р. И если материал будет иметь ν > 0,5, тело увеличит свой объём, что невозможно. Опыты подтверждают это положение: в природе не существует материала с коэффициентом Пуассона, большим 0,5.

3.6. Потенциальная энергия упругой деформации

Как отмечалось выше (см. п. 2.8), в процессе упругой деформации в теле накапливается потенциальная энергия, равная работе внешних сил. При осевом растяжении (линейном напряжённом состоянии) удельная потенциальная энергия (т.е. энергия, приходящаяся на единицу объёма) определяется по формуле (2.37)

.

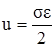В общем случае объёмного напряженного состояния

. (3.32)

Подставив значения ε по формуле (3.25), получим

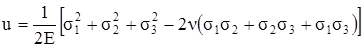. (3.33)

Экспериментальные исследования показали, что прочность материала зависит не только от величины компонентов напряжений, но и от характера напряжённого состояния. Так, большинство твёрдых тел противостоит без разрушения действию очень большого всестороннего давления – при этом изменяется объём бесконечно малого элемента. И наоборот, те же тела разрушаются при сравнительно невысоких напряжениях, если эти напряжения изменяют форму элемента. Поэтому полную потенциальную энергию упругой деформации, определяемую по формуле (3.33), представляют в виде суммы двух составляющих:

u = u₀ + u_ф, (3.34)

где u₀ – удельная потенциальная энергия изменения объёма, т.е. энергия, накапливаемая за счёт изменения объёма;

u_ф – удельная потенциальная энергия формоизменения, т.е. энергия, накапливаемая вследствие изменения формы элемента.

Для определения этих составляющих заданное напряжённое состояние представим в виде суммы двух напряжённых состояний (рис.3.15): изменяющего объём элементарного кубика (гидростатическое растяжение одинаковыми средними напряжениями) и изменяющего форму кубика.

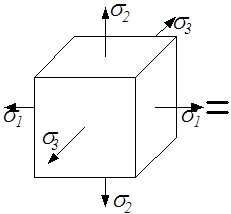
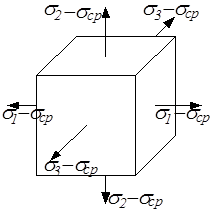
Рис. 3.15

Чтобы найти u₀, в формулу (3.33) подставим σ₁ = σ₂ = σ₃ = σ_ср и получим:

. (3.35)

Подставив в (3.35) значение σ_ср = (σ₁ + σ₂ + σ₃)/3, получим окончательное выражение для удельной потенциальной энергии изменения объёма

. (3.36)

Удельную потенциальную энергию формоизменения найдём простым вычитанием:

u_ф = u – u₀.

Необходимо из (3.33) вычесть (3.36):

(3.37)

Итак, удельная потенциальная энергия формоизменения определяется по формуле

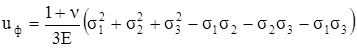. (3.38)

Из (3.38) легко получить выражения для u_ф при плоском напряжённом состоянии (σ₂ = 0)

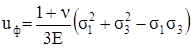, (3.39)

и при линейном напряжённом состоянии (σ₂ = σ₃ = 0)

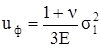. (3.40)

3.7. Теории прочности

3.7.1. Задачи теорий прочности

Важнейшей задачей инженерного расчёта является оценка прочности детали по известному напряжённому состоянию, т.е. по известным главным напряжениям в точках тела.

Материал детали может находиться в различных состояниях. При малых внешних нагрузках материал находится в упругом состоянии. При увеличении внешних сил с определённого момента появляются заметные остаточные деформации и, следовательно, материал переходит в пластическое состояние. При дальнейшем увеличении внешних сил появляются трещины и наступает состояние разрушения. Механическое состояние зависит в первую очередь от напряжённого состояния, а также от ряда других факторов – температуры, времени нагружения и прочих второстепенных факторов.

Предельным (опасным) считается такое напряжённое состояние, при котором происходит качественное изменение свойств материала: переход из упругого состояния в пластическое или переход из упругого в состояние разрушения. Опасные напряжения находятся экспериментально - в процессе лабораторных испытаний материала. Наиболее просто задача определения опасных напряжений решается при стандартных испытаниях на растяжение или сжатие: для пластичного материала это предел текучести σ₀ = σ_т, для хрупкого – предел прочности σ_оп = σ_пч. Образцы при этом находятся в линейном напряжённом состоянии (см. п. 2.6.1 и 2.6.2). Не намного сложнее определить опасные напряжения в частном случае плоского напряжённого состояния – при чистом сдвиге. Чистый сдвиг – это такое напряжённое состояние, при котором по некоторым взаимно перпендикулярным площадкам действуют только касательные напряжения. При испытании на кручение тонкостенной трубы нетрудно установить величины опасных напряжений по характерным точкам диаграммы.

Если следовать по указанному пути, то для каждого напряжённого состояния, определяемого тремя величинами главных напряжений, и для каждого материала необходимо иметь соответствующие диаграммы испытаний с числовыми характеристиками предельных точек. Однако такой путь является абсолютно неприемлемым в силу неисчерпаемости типов напряжённых состояний, а также в связи с техническими трудностями постановки соответствующих испытаний.

Поэтому необходимо создать такую методику расчёта, которая позволяла бы оценить степень опасности любого сложного напряжённого состояния, основываясь на результатах опытов при простом растяжении или сжатии. Эта задача решается с помощью так называемых теорий прочности (точнее, теорий предельных напряжённых состояний).

Для этого вводят гипотезу о преимущественном влиянии на прочность того или иного фактора – критерий прочности. Считают, что наступление предельного состояния при объёмном напряжённом состоянии произойдёт тогда, когда величина критерия прочности достигнет предельного значения. Предельное же значение этого критерия, "ответственного" за наступление опасного состояния, находят на основании простых стандартных опытов на растяжение – сжатие (кручение).

Таким образом, введение критерия прочности позволяет сопоставить данное сложное напряжённое состояние (плоское или объёмное) с простым линейным, и установить при этом такое расчётное (эквивалентное) напряжение, которое в обоих случаях даёт одинаковый коэффициент запаса прочности.

3.7.2. Классические теории прочности

Первая (I) теория прочности – теория наибольших нормальных напряжений. Наиболее простая теория прочности, ведущая своё начало от Галилея. Критерием прочности, "ответственным" за наступление опасного состояния является наибольшее из трёх главных напряжений.

Условие нарушения прочности имеет вид

σ₁ = σ_оп⁺ = σ_т, σ₃ = σ_оп^- = σ_пч. (3.41)

Если правую часть выражений (3.41) поделить на коэффициент запаса, получим условие прочности:

σ^I_расч = σ₁ ≤ [σ₊], σ^I_расч = |σ₃| ≤ [σ_-]. (3.42)

Первая теория прочности из трёх главных напряжений учитывает лишь одно- наибольшее, полагая, что два других не влияют на прочность. Это явный недостаток этой теории.

Опытная проверка показывает, что I-я теория прочности не отражает переход материала в пластическое состояние и даёт удовлетворительные результаты лишь для весьма хрупких материалов.

Вторая (II) теория прочности – теория наибольших линейных деформаций. Идею второй теории прочности впервые высказал Мариотт: критерием прочности, "ответственным" за наступление опасного состояния, является наибольшая по абсолютной величине относительная линейная деформация.

Условие разрушения следующее:

|ε_max| = ε_оп, (3.43)

а условие прочности

. (3.44)

Используя обобщённый закон Гука (3.25), выразим условие прочности (3.44) в напряжениях. Пусть наибольшее относительное удлинение будет ε₁. Тогд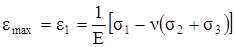а

. (а)

При простом растяжении, приняв в качестве допускаемого напряжения [σ], мы тем самым для наибольшего относительного удлинения допускаем величину

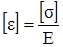. (б)

Подставив (а) и (б) в условие прочности (3.44) и, сократив на E, получим окончательное выражение для условия прочности по II - й теории прочности

σ^II_расч = σ₁ – ν (σ₂ + σ₃) ≤ [σ]. (3.45)

В отличие от I-й теории прочности учитываются все три главных напряжения. Однако, опытная проверка указывает на согласующиеся результаты лишь для хрупких материалов.

Третья (III) теория прочности – теория наибольших касательных напряжений. В этой теории, предложенной Кулоном в 1773 году, в качестве фактора, "ответственного" за наступление опасного состояния, принято наибольшее касательное напряжение.

Условия разрушения и прочности имеют вид

τ_max = τ_оп. (3.46)

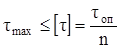. (3.47)

Так как согласно (3.21)

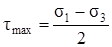, а ,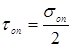

то условия разрушения и прочности (3.46) и (3.47) можно выразить через главные напряжения:

σ₁ – σ₃ = σ_оп, (3.48)

σ^III_расч = σ₁ – σ₃ ≤ [σ]. (3.49)

Третья теория прочности хорошо подтверждается опытами для материалов, одинаково работающих на растяжение и сжатие. Она предназначена для прогнозирования предельного состояния в форме течения, т.е. для пластичных материалов. Недостаток третьей теории заключается в том, что она не учитывает среднего по величине главного напряжения σ₂, которое, как показывают опыты, оказывает некоторое влияние (хотя во многих случаях и незначительное) на прочность материала. Условие прочности в форме (3.49) нашло широкое применение в инженерной практике.

Четвёртая (IV) теория прочности – энергетическая. В основу этой теории, предложенной Мизесом в 1913 году, положен постулат о том, что причиной наступления предельного состояния в форме течения является удельная потенциальная энергия изменения формы, а не напряжения или деформации. Следовательно, математической моделью энергетической теории является следующее условие

u_ф = u_оп. (3.50)

Подставляя в (3.50) значения u_ф при объёмном напряжённом состоянии по формуле (3.38) и при линейном напряжённом состоянии по формуле (3.40), получим условие наступления предельного состояния

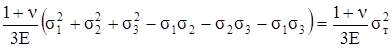, (3.51)

где σ_т – предел текучести.

Сокращая на множитель с упругими постоянными и записывая в правой части допу

Дата добавления: 2014-01-05