И в перпендикулярном направлении

Модули нормальной упругости в направлении оси волокна

Рассмотрим, как рассчитать модули упругости армированных КМ по известным упругим характеристикам и объемным концентрациям его компонентов. Остановимся на простейшем случае КМ – параллельно уложенные в одном направлении армирующие элементы, связанные между собой матричными прослойками (рис. 2.1). Пластины (монослои) таких материалов – основа для получения различных слоистых КМ, а по известным характеристикам однонаправленных композиций можно рассчитывать свойства композиций с различной ориентацией волокон в смежных слоях. Поэтому в дальнейшем основное внимание будем уделять свойствам однонаправленных КМ. Такие материалы трансверсально изотропны.

Основные допущения, применяемые в расчете, сводятся к тому, что и волокна и матрица – изотропные упругие материалы, которые при нагружении КМ деформируются совместно (это обеспечивается наличием между ними жесткой связи).

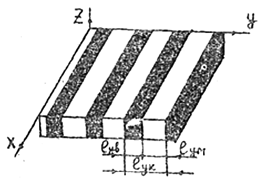
Рис. 2.1. Схематическое изображение структуры однонаправленных КМ (черные области – волокна, белые – матрица)

Нагрузим рассматриваемую пластину силой Р_х. При этом относительная деформация e_хк композиции в направлении оси х в силу совместимости деформаций матрицы и волокна будет равна деформации матрицы e_хм и волокон e_хв:

(2.1)

Сумма сил, действующих на матрицу Р_хм и на волокно Р_хв, равна общей силе Р_х:

(2.2)

Воспользовавшись тем, что силу можно представить как произведение напряжения на площадь поперечного сечения, равенство (2.2) перепишем в виде

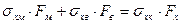(2.3)

где:

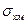,и – растягивающие напряжения в матрице, волокне и всей композиции в направлении оси х соответственно:

,и 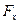– поперечные сечения матрицы, волокна и КМ, соответственно.

Разделив обе части равенства (2.3) на F_к, получим

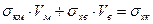(2.4)

где:

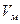,– объемная доля матрицы и волокна в КМ соответственно;

; ; .

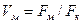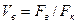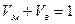Закон Гука для одноосного напряженного состояния позволяет записать:

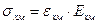; ; (2.5)

Здесь 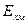,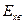и 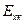– модули Юнга матрицы, волокна и композиции в направлении х соответственно. Поскольку материалы матрицы и волокон приняты изотропными, то в дальнейшем индексы направления у характеристик этих материалов будем опускать и использовать только индексы м и в.

Если вместо напряжений в уравнение (2.4) подставить их выражения из уравнения (2.5) и воспользоваться условием (2.1), то можно получить выражение для определения модуля нормальной упругости в направление оси волокон Е_хк:

(2.6)

Это выражение позволяет определить модуль нормальной упругости однонаправленного армированного КМ в направлении армирования по известным концентрациям и модулям упругости матрицы и волокон.

Рассмотрим поведение модели (рис. 2.1) при нагружении ее силой, перпендикулярной к оси волокон. В этом случае напряжения в каждом из компонентов будут одинаковыми:

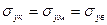(2.7)

а абсолютная деформация D_ук всей композиции будет равна сумме абсолютных деформаций матрицы D_ум и волокон D_ув:

(2.8)

Абсолютная деформация связана с относительной соотношением

где:

l – длина деформируемого элемента.

Из уравнения (2.8) получаем

(2.9)

где:

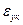,и 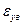– относительные деформации композиции, матрицы и волокна в направлении оси у соответственно;

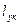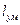,и 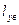– длина рассматриваемого элемента КМ, суммарная длина матричных прослоек и волокон в направлении у соответственно.

Если для упрощения принять, что сечения волокон прямоугольные, то

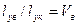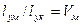, (2.10)

Разделив обе части уравнения (2.9) на l_ук с учетом зависимостей (2.10) получим

(2.11)

Согласно закону Гука, (относительная деформация равна частному от деления напряжений на модуль упругости). С учетом равенства (2.7) получим:

(2.12)

Дата добавления: 2014-01-05