Влияние ориентации волокон на прочность КМ

В технике обычно использую анизотропные КМ с определенной симметрией свойств. При изучении их физико-механических характеристик реальный, как правило, весьма неоднородный материал представляют в виде идеализированной сплошной однородной среды с симметрией строения и свойств. Наиболее часто важные ориентированные КМ удается представить как ортотропные или как трансверсально изотропные среды.

Рассмотрим прочность однонаправленного КМ при воздействии растягивающих напряжений σ, приложенных под углом θ к направлению волокон (рис. 2.8). В зависимости от величины θ возможны три механизма разрушения КМ.

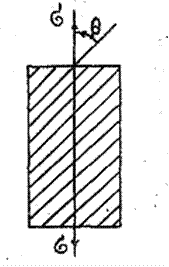
Рис. 2.8. Схема погружения однонаправленных КМ под углом θ к оси волокон

1. При малых θ материал разрушается в результате разрыва волокон от нормальных напряжений в результате течения матрицы параллельно волокнам. Если прочностью матрицы пренебречь, то нормальные напряжения σ_н в волокнах определятся как отношение силы Р_н, действующей в направлении θ (Р_н = σ·F·cos θ, где F – площадь сечения, перпендикулярного к направлению действия внешнего напряжения θ), к площади Р_н сечения, перпендикулярного к оси волокон (F_н = F/соs θ), откуда

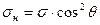(2.25)

Предел прочности σ_в КМ в рассматриваемом случае можно рассчитать из уравнения (2.25), если положить σ_н = σ_вв, где σ_вв – предел прочности волокон:

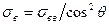(2.26)

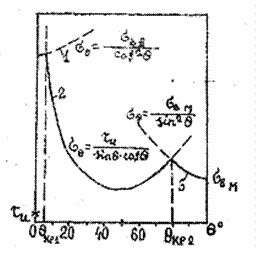
Рис. 2.9. Зависимость предела прочности однонаправленного КМ от ориентации волокон по уравнениям: 1 – (2.26); 2 – (2.27); 3 – (2.28)

Если углы θ малы (рис. 2.9 кривая 1), с ростом θ прочность может увеличиваться. Эксперименты показывают, что эти углы не превышают нескольких градусов.

2. Начиная с критического значения θ_кр1 прочность КМ определяется вторым механизмом – разрушением матрицы или границы раздела волокно-матрица в результате сдвига по плоскостям, параллельным волокнам. Сдвиговые напряжения τ на этих плоскостях определяются соотношением τ = σ·cosθ·sinθ, а прочность σ_в КМ формулой:

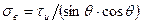(2.27)

где:

τ_u – предел прочности матрицы или границы раздела при сдвиге.

Зависимости σ_в от θ при действии второго механизма разрушения соответствует кривая 2 на рис 2.9 Минимум прочности соответствует углу θ = 45°.

Значение θ_кр1 определяется абсциссой точки пересечения кривых 7 и 2 и может быть рассчитана приравниванием выражений (2.26) и (2:27):

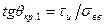
3. При больших значениях θ прочности КМ характеризуется третьим видом разрушения (рис. 2.9, кривая 3), который определяется нормальной прочностью матрицы или границы раздела в направлении, перпендикулярном к волокнам. Прочность КМ в этом случае выражается соотношением:

(2.28)

где:

σ_вм – предел прочности матрицы в условиях плоской деформации.

Значение θ_кр.2, соответствующее смене второго механизма разрушения третьим, определяют, приравнивая выражения (2.27) и (2.28):

Чем больше отношение нормальной прочности матрицы к ее сдвиговой прочности, тем больше θ_кр.2.

Дата добавления: 2014-01-05