Правило смесей. Прочность в направлении армирования для КМ, упроченных параллельными отрезками волокон, можно оценить по правилу смесей с учетом концевого эффекта

Прочность в направлении армирования для КМ, упроченных параллельными отрезками волокон, можно оценить по правилу смесей с учетом концевого эффекта. Рассмотрим, какое влияние оказывает длина волокон на средние растягивающие напряжения σ_в в них.

Рис. 2.11. Эпюры растягивающих напряжений в волокнах различной длины

1. При l < l_кр по мере увеличения длины волокна растет как максимальное растягивающее напряжение (действует посредине волокна), так и среднее растягивающее напряжение 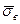в волокнах, которое можно рассчитать по формуле

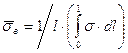
Без большой ошибки можно допустить, что нормальные напряжения в волокнах растут от концов волокна к его середине по линейному закону (рис. 2.11). Тогда при l < l_кр эпюры напряжений имеют вид, изображенный для волокон с длинами l₁ и l₂ (рис. 2.11, а, б). Максимальное напряжение изображено штриховой линией, среднее – штрихпунктирной. В этих случаях максимальные напряжения в волокнах не достигают их предела прочности и среднее нормальное напряжение.

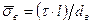
Разрушаются такие КМ из-за вытягивания волокон из них. При этом среднее растягивающее напряжение в волокнах в момент разрушения КМ равно (τ_г.р·l)/d_в уравнение аддитивности (2.19) принимает вид:

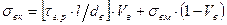
Таким образом, если l < l_кр, то прочность однонаправленных КМ растет пропорционально объемной доле волокон, отношению l/d_в прочности границы раздела и прочности матрицы, оставаясь при этом меньше прочности КМ, армированных непрерывными волокнами.

2. При l ³ l_кр, когда длина волокна становится равной l_кр, максимальное нормальное напряжение в средней части волокна достигает значения, равного растягивающему напряжению 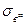в бесконечно длинном волокне (рис. 2.11, в). При дальнейшем увеличении l (рис. 2.11. г) максимальное напряжение в волокне остается неизменным (равным 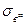), но увеличиваются участки волокон, на которых действует это напряжение. Следовательно, растут и средние напряжения 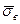, т.е. для волокон длиной l₁ < l₂ < l_кр < l₄ имеет место соотношение <<<.

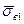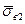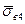Запишем среднее растягивающее напряжение волокна на концевых участках длиной 0...l_кр/2 в виде произведения 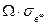, где W – коэффициент, меньший 1. Доля этих участков, на которых действует напряжение 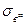, составляет V_в·(l – l_кр)/l.

Напряжение 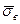, усредненное по всей длине волокон, можно определить следующим образом:

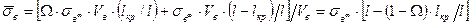
Если растягивающее напряжение от концов волокон растет линейно, то W = 0,5. Тогда среднее напряжение в волокнах

.

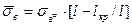В соответствии с правилом аддитивности, общее напряжение, приложенное к КМ, равно сумме средних напряжений в матрице и волокнах. Для КМ с дискретными волокнами, имеющими l > l_кр, можно записать:

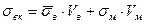(2.30)

В момент разрушения 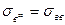, а .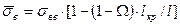

Подставив последнее значение вместо 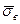в уравнение (2.30) и заменив в нём напряжение в матрице напряжением 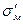, получим, формулу для оценки прочности КМ, армированных дискретными волокнами, которая наряду с влиянием объемной доли волокон учитывает и влияние их длины:

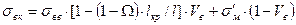(2.31)

Как и при армировании непрерывными волокнами, предел прочности композиции с короткими волокнами растет пропорционально V_в, если V_в > V_min. С увеличением соотношения l/l_кр прочность КМ растет, приближаясь к прочности композиций с непрерывными волокнами (l/l_кр = ¥).

Сопоставив между собой уравнения (2.19) и (2.31) и приняв в последнем W» 0,5, получим соотношение между прочностями КМ, упрочненных дискретными 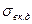и непрерывными 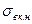волокнами:

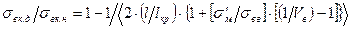
Как показывают расчеты, уже при l/l_кр = 10 прочность КМ с дискретными волокнами достигает 95% прочности КМ с непрерывными волокнами, что позволяет получить практически ту же прочность композиций, что и при армировании непрерывными волокнами, если отрезки волокон достаточно длины.

Минимальную и критическую долю дискретных волокон в КМ рассчитывают так же, как и непрерывных волокон, например,

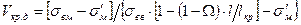
Доли V_кр.д и V_min.д всегда больше, чем соответствующие значения V_кр.н и V_min.н. Например, если КМ состоит из алюминия, армированного волокнами с σ_вв = 70 кгс/мм², то V_кр.н = 8,3%; а доля V_кр.д = 17,4% при l/l_кр = 1.

Дата добавления: 2014-01-05