Прочность пучка волокон

Вначале рассмотрим, как зависит вероятность разрушения одного волокна от его длины.

Волокно длиной l мысленно разделим на равные отрезки, длина которых равна диаметру d_в волокна. Число таких отрезков

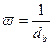
Всегда имеющиеся в волокне дефекты (они могут появиться при получении или при нагружении волокон) статистически распределены по всей длине. Наличие их определяет прочность каждого отрезка.

Совокупность прочностей отрезков можно охарактеризовать функцией распределения f(σ), в которой f(σ)·dσ – вероятность того, что данный отрезок разрушится в интервале напряжений σ...σ + dσ.

Вероятность того, что все отрезки разрушатся при напряжении, меньшем определенного уравнения σ, выразится интегральной функцией распределения прочности

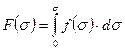
Понятно, что при напряжении, меньшем σ, вероятность неразрушения любого отрезка составит 1 – F(d), ибо разрушение и неразрушение волокна – события противоположные.

Представим теперь, что все волокно ведет себя как цепь, составленная из ω звеньев (отрезков). Разрушится оно, когда разрушится одно слабейшее звено этой цепи. Вероятность этого разрушения в интервале растягивающих напряжений σ...σ + dσ характеризуется дифференциальной функцией распределения g(σ). При напряжениях, меньших или равных σ, вероятность неразрушения в этом же интервале остальных (ω – 1) звеньев по правилу умножения вероятностей будет равна [1 – F(σ)]^{w – 1} (Предлагается, что разрушение каждого звена не зависит от разрушения остальных звеньев). Поскольку волокно разрушается при разрыве одного любого звена, то дифференциальная функция распределения вероятности g(σ) разрушения волокна в диапазоне напряжений σ...σ + dσ равна:

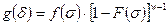
Вероятность же разрушения всего волокна в интервале напряжений 0...σ определяется интегральной функцией G(σ) распределения прочности волокон:

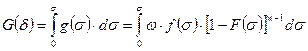
Проинтегрировав это уравнение, получим:

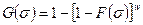(2.35)

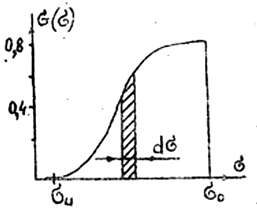
Рис. 2.14. Функция распределения прочности стекловолокна

Это выражение позволяет по известной интегральной функции распределении прочности звена F(σ) определить интегральную функцию распределения прочности волокна G(σ). На основе анализа многочисленных экспериментальных данных о прочности материалов Вейбулл предложил задавать функцию F(σ) выражением:

где:

σ – напряжение, приложенное к волокнам, значение которого находится в интервале между пределами прочности нижним σ_и и верхним σ₀ (рис. 2.14)

m – параметр, характеризующий разброс данных (параметр Вейбулла).

Часто в качестве нижнего предела прочности принимают σ_и = 0. Тогда σ₀ становится равной теоретической прочности материала. Отклонение прочности волокон от среднего значения (характеризуемое коэффициентом вариации С, можно рассчитать по дисперсии прочности S и средней прочности испытанной партии материалов или с помощью параметра m.

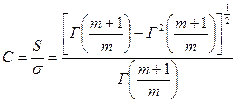(2.37)

где:

Г[(m + 1)/m] – табулированная гамма-функция;

S – равна квадрату стандартного отклонения прочности.

;

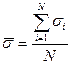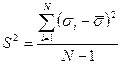
где:

σ_i – прочность i -го образца;

N – число испытанных образцов.

Приближенно зависимость (2.37) можно аппроксимировать более простым выражением:

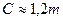(2.38)

Чем больше m, тем меньше разброс прочности материала. При m ® ¥ разброса нет.

Подставив выражение (2.36) в уравнение (2.35), получаем

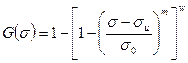(2.39)

Для малых значений х = σ – σ_и/σ₀ можно воспользоваться приближением Пуассона

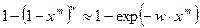(2.40)

и, используя зависимость (2.30) привести выражение (2.39) к более удобному для вычислений виду:

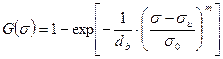(2.41)

Таким образом, вероятность разрушения волокна при заданном напряжении σ возрастает по мере увеличения отношения 1/d_в. Параметры σ_и, σ₀ и m уравнения Вайбулла рассчитывают по результатам механических испытаний партии волокон.

Определим теперь прочность пучка волокон длиной l. Будем считать, что все волокна в пучке параллельны, не касаются друг друга и нагружаются одинаково.

Если из всех N испытанных волокон n волокон разрушилось при напряжениях, меньших σ, а общая нагрузка, приложенная к пучку, равна Р_в, то напряжение в уцелевших волокнах находится по формуле

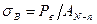
где:

А_{N – n} – суммарная площадь сечений неразрушившихся волокон. Так как

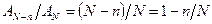, то ,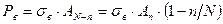

где:

.

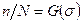Тогда, используя уравнение (2.41) получим

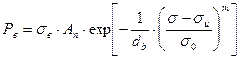
Нагрузка на пучок волокон достигает максимума при dР_в/dσ_в = 0. Приняв для упрощения σ_п = 0 и проведя преобразования последнего выражения, определим максимальную нагрузку на пучок волокон:

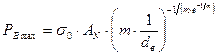
где:

е – основание натуральных логарифмов.

Прочность пучка волокон σ_пуч равна отношению максимальной нагрузки к площади поперечного сечения А_N всех исходных волокон:

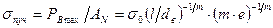(2.42)

Это уравнение устанавливает зависимость прочности пучка от отношения длины волокон к диаметру и параметра m, характеризующего разброс данных. Чем больше 1/d_в, тем меньше прочность пучка волокон.

Среднюю прочность отдельно испытанных волокон σ можно рассчитать по известным σ₀ и m:

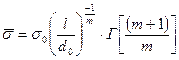; (2.43)

где:

Г[(m + 1)/m] – гамма-функция.

Разделив выражение (2.41) на зависимость (2.42), получим

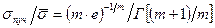(2.44)

Таким образом, с увеличением m, т.е. с уменьшением разброса, отношение 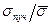растет. Иными словами, прочность пучка снижается быстрее, чем средняя прочность партии отдельно испытанных волокон. Обычно m = 2...5 соответствует хрупким материалам, а m» 15...20 – пластичным.

На практике отношение прочности пучка к средней прочности одного волокна оказывается ниже, чем рассчитанное по уравнению (2.44). Это связано с невозможностью равномерно нагрузить все волокна и обеспечить их полную параллельность.

Дата добавления: 2014-01-05