Трехточечный изгиб

Изгиб

Сдвиг

Сжатие

Прочность и жесткость анизотропных армированных материалов при сжатии определяют по тем же формулам, что и при растяжении. Однако простота и аналогия с растяжением здесь только кажущиеся, так как механизмы разрушения КМ при сжатии и растяжении отличаются друг от друга.

Одна из основных причин разрушения армированных материалов под действием сжимающих нагрузок – это потеря устойчивости волокнами. Она может произойти из-за слабого сопротивления КМ сдвиговым напряжением, либо из-за выпучивания слоев арматуры, расположенных вблизи боковых поверхностей образца. В последнем случае на диаграммах Р-Dl наблюдаются характерные переломы и использование таких диаграмм для определения показателей жесткости и прочности может привести к ошибочным результатам. Значительно исказить результаты может неточная установка образцов, неправильный выбор их размеров и формы, приводящие к неоднородному напряженному состоянию в рабочей части образца.

Подход к определению прочности и упругих констант при сжатии должен быть дифференцированным. Определяя модули упругости, используют длинные образцы, имеющие достаточно однородное поле напряжений в рабочей части. Для определения прочности можно применять более короткие образцы (рис. 3.4), хотя и в этом случае размеры их могут влиять на показатели прочности. У образцов в форме куба со стороной 12 мм прочность при сжатии оказывается в 1,5 раза ниже, чем у образцов в виде тонких пластин 78x18x2, и почти в 2 раза ниже, чем у образцов - лопаток таких же размеров. Объясняется это тем, что в коротких образцах деформации по длине рабочей части неравномерны, поперечная деформация образцов стеснена трением в опорных поверхностях. В длинных же образцах ограничение деформации в опорах значительно меньше влияет на поведение материала в рабочей зоне.

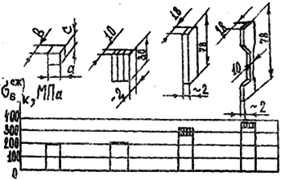
Рис. З.4. Прочность при сжатии (σ_в^сж)_к образцов разной формы (заштрихован разброс экспериментальных данных)

При испытаниях на сжатие применяют параллелепипеды, двусторонние лопатки и образцы с круглым поперечным сечением. Рекомендации по выбору размеров образцов есть только для полимерных КМ.

Образцы-параллелепипеды следует применять, измеряя в условиях сравнительно небольших нагрузок упругие постоянные материалов, нагружаемых вдоль главных осей. Ширину b выбирают в диапазоне 13...30мм, длину l рассчитывают так, чтобы гибкость образца находилась в интервале 11...15 { J_min – минимальный момент инерции; F – площадь поперечного сечения образца). Чтобы предотвратить смятие концов образца, на них наклеивают накладки, материал которых выбирают так же, как и при испытаниях на растяжение.

Образцы-параллелепипеды используют и для определения характеристик при сжатии образцов с ориентацией волокон под углом 45° к сжимающей нагрузке. В этом случае, чтобы устранить влияние концевых эффектов, нужно выдержать соотношение l/b ³ 3.

Двусторонние лопатки типа изображенных на рис. 3.2. имеют четко выраженную рабочую часть. Их используют, измеряя жесткость и прочность КМ с различной ориентацией арматуры. При испытаниях тонких образцов для предотвращения их выпучивания применяют специальные приспособления, поддерживающие широкие поверхности образца призматическими выступами или мягкими наполнителями, не стесняя деформации в другом поперечном направлении. Чтобы исключить смятие торцов, на концы образца иногда наклеивают тонкие металлические накладки или наконечники.

Наконечники из металла или других материалов используют и при испытаниях образцов с круглым поперечным сечением, которые обеспечивают меньший разброс значений прочности и жесткости. Такие образцы применяют обычно, испытывая армированные металлы и легко обрабатываемые полимерные КМ (например, углепластики).

При испытании на сжатие очень важно обеспечить параллельность торцов. Тангенс угла между осью образца и направлением приложения нагрузки не должен превышать 0,001. Как правило, у полимерных и металлических КМ твердость волокон значительно больше твердости матрицы, из-за чего удается получить гладкие опорные поверхности образца – концы волокон выступают над поверхностью матрицы. Чтобы обеспечить полный контакт между торцами образца и пуансоном испытательной установки, рекомендуется изготовлять пуансоны из мягкой стали. Применение наконечников на образцах также способствует улучшению условий испытаний.

Прочность некоторых КМ при сжатии ниже, чем при растяжении, так как при сжатии тонкие волокна не успевают полностью реализовать свою высокую прочность из-за потери устойчивости. Но, если диаметр волокон большой (100 мкм и более) и они имеют высокую жесткость, а следовательно, и хорошую устойчивость, прочность КМ при сжатии может оказаться выше, чем при растяжении, как это и имеет место у боропластиков.

КМ на полимерной и металлической основах обычно состоят из сравнительно малопрочной, низкомодульной матрицы и высокопрочных, высокомодульных волокон. Для такого типа материалов характерно слабое сопротивление сдвиговым напряжением. В первую очередь это относится к армированным пластикам.

Рис 3.5. Схема сдвига в КМ с ориентированной структурой; а – в плоскости укладки арматуры (τ_ху = τ_ух); б- межслойного (τ_хz = τ_zх)

В КМ с ориентированной структурой различают два вида сдвиговых деформаций (рис. 3.5): сдвиг в плоскости укладки арматуры, происходящей под действием касательных напряжений τ_ху и τ_ух (рис. 3.5, а), и межслойный сдвиг, обусловленный действием касательных напряжений τ_хz и τ_zх (рис. 3.5, б). Основное влияние на модули сдвига и сдвиговую прочность оказывает матрица.

Рис. 3.6. Образец (а) и стандартный шарнирный четырехзвенник (б) для испытания армированных материалов на сдвиг: 1 – образец; 2 – захват; 3 – ось шарнира; 4 – подвижное звено

При испытаниях на сдвиг в плоскости укладки арматуры определяют модуль сдвига G_xy и сдвиговую прочность τ_ху. Один из наиболее распространенных методов определения их – метод перекашивания пластин в шарнирном четырехзвеннике (рис. 3.6) Крестообразную пластину - образец (рис. 3.6, а) закрепляют шпильками с 4-х сторон в шарнирном четырехзвеннике (рис. 3.6, б), который растягивается силой Р вдоль одной из диагоналей пластины. Модуль сдвига G_ху определяют по формуле:

,

где:

Р – растягивающая нагрузка;

а – размер стороны рабочей части пластины (сторона а = 100 мм);

h – толщина рабочей пластины;

e₁ и e₂ – относительные деформации пластины вдоль диагоналей растяжения и сжатия соответственно.

Сдвиговую прочность τ_ху в плоскости листа рассчитывают из соотношения:

.

У рассмотренных конструкций образца и четырехзвенника есть существенный недостаток – в углах рабочей части возникает концентрация напряжений, а у мест крепления возможно выпучивание образцов. При испытаниях сильно анизотропных материалов это приводит к погрешностям. Для таких материалов лучше изготовить образцы в виде пластин с пропилами, а испытания проводить на несколько модернизированных четырехзвенниках.

Изгибными испытаниями изотропных материалов обычно определяют модуль упругости Е_и и предел прочности σ_и при изгибе. При этом используют известные из курса сопротивления материалов зависимости между экспериментально замеряемыми нагрузками Р и соответствующими им прогибами ω образцов - балок. Например, при трехточечном изгибе стержня (рис. 3.7, а) модуль Е_и и прочность σ_и определяют по формуле:

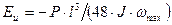; (3.1)

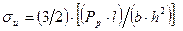, (3.2)

где:

Р – текущая нагрузка, соответствующая прогибу ω_mах в середине пролета балки;

l – расстояние между опорами;

b – ширина образца;

h – его высота;

J – момент инерции поперечного сечения стержня.

Кроме нормальных, в изгибаемой банке действуют и касательные напряжения, влияние которых на прочность и жесткость изотропных материалов пренебрежимо мало.

Уравнения (3.1) и (3.2) не учитывают возможность межслойных сдвигов, поскольку для изотропного материала само понятие слоев не имеет смысла – он равнопрочен во всех направлениях. Наблюдаемая на практике некоторая анизотропия свойств у реальных гомогенных материалов, связанная с влиянием пластической деформации, неравномерной кристаллизацией и т.п., обычно выражена значительно слабее, чем у армированных материалов, и ею при использовании указанных зависимостей можно пренебречь. Композиционный армированный материал представляет собой по сути дела составную к6нструкцию, одним из слабых мест которой является низкая сдвиговая жесткость и прочность в некоторых направлениях. Поэтому применение к ним обычных формул теории изгиба, не учитывающих структурных особенностей, может привести к грубым ошибкам.

Разрушение изотропных материалов при изгибе как правило происходит под действием нормальных напряжений. Армированные анизотропные композиции при трехточечном изгибе в зависимости от размеров образца могут разрушаться как от нормальных, так и от касательных напряжений. В последнем случае формула (3.2) для определения прочности не применима, поскольку фактически определяется уже не прочность при изгибе, а прочность τ_сдв при межслойном сдвиге, равная

(3.3)

Таким образом, при изгибных испытаниях в зависимости от характера разрушения образца можно определить прочность или по касательным, или по нормальным напряжениям. На практике в образце всегда действуют оба вида напряжений и для анизотропных материалов, определяя свойства при изгибе, следует учитывать их взаимное влияние.

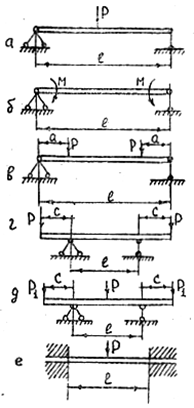
Рис. 3.7. Схемы нагружения образцов при испытании на изгиб: а – трехточечная; б – чистый изгиб; в, г – четырехточечные; д – пятиточечная; е – с защемленными концами

Рассмотрим существующие методы испытаний КМ на изгиб.

Наиболее распространен такой его вид, когда свободно опирающийся на две опоры образец нагружен в середине пролета сосредоточенной силой Р (рис. 3.7, а). Рассчитывая модуль упругости слоистых КМ, следует пользоваться уточненными зависимостями, учитывающими влияние сдвиговых, деформаций и связывающими максимальный прогиб сотах балки посредине пролета с приложенной силой Р, истинным модулем упругости Е_{и ист} и модулем межслойного сдвига G_м.с.:

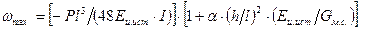(З.4)

где:

α – коэффициент, зависящий от формы поперечного сечения балки (для прямоугольного сечения α» 1,2);

остальные обозначения те же, что и в уравнении (3.1).

Сопоставив уравнения (3.1) и (3.4), заметим, что истинный модуль Е_{и ист} связан с фиктивным модулем Е_и соотношением

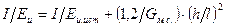(3.5)

Чем больше h/ l образца и чем больше степень анизотропии материала, характеризуемая отношением Е_{и ист}/G_м.с., тем больше истинный модуль упругости Е_{и ист} отличается от фиктивного Е_и.

Для трехточечного изгиба удобнее уравнение (3.1) привести к виду

(3.6.)

так как

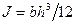
где:

J – момент инерции поперечного сечения балки.

В результате единичного эксперимента по уравнению (3.4) модуль упругости вычислить нельзя, поскольку оно содержит две неизвестные величины: Е_{и ист} и G_м.с. (в процессе испытания замеряют ω_mах и P). Чтобы получить значение Е_{и ист} и G_м.с., испытаниям подвергают несколько образцов одного и того же КМ с разным отношением h/l, а затем строят график зависимости Е_и от h/l (рис. 3.8). В приведенных на графике координатах зависимость (4) изображается прямой, пересекающей ось ординат в точке, соответствующей 1/Е_{и ист}; а тангенс угла наклона этой прямой к оси абсцисс равен 1,2/G_м.с..

Рис. 3.8. Результаты экспериментов по определению модуля упругости (Е_и) и модуля межслойного сдвига (G_м.с.) для стектекстолита ЭФ32-З01 и 6оропластиков (б) (укладка волокон у боропластиков: 1 – 1:1:1; 2 – 1:1; 3 – 2:1; 4 – 1:0)

Аналитически по результатам экспериментов значения Е_{и ист} и G_м.с. определяют с помощью метода наименьших квадратов:

(3.7)

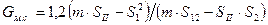(3.8)

где:

; ;

; .

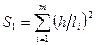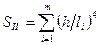Е_иi определяется по формуле (3.1) или (3.6).

m – число экспериментальных точек, равное сумме всех замеров h_n/l_i (здесь n – число измерений прогиба при h/l_i = const).

Другой способ вычисления модулей упругости Е_{и ист} и G_м.с. заключается в построении графика в координатах 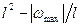, который в соответствии с уравнением (3.4) должен представлять собой прямую линию. При этом испытывают партию образцов одинакового поперечного сечения, но различной длины l. Отрезок, отсекаемый прямой от оси абсцисс равен Р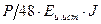. Значения Е_{и ист} и G_м.с. находят или графически, или по методу наименьших квадратов.

Уточненные формулы для расчета максимальных нормальных и сдвиговых напряжений при изгибе следующие:

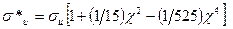; (3.9)

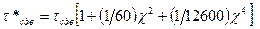. (3.10)

σ_и и τ_сдв определяются по формулам (3.2) и (3.3) соответственно;

– параметр анизотропии.

Различие в результатах, подученных при использовании формул (3.2) и (3.9), (3.3) и (3.10) существенно только для КМ с очень большой конструкционной анизотропией (например, для боро- и углепластиков) и при больших отношениях h/l. Если величина c < 1,2, то без ущерба для практической точности можно вести расчет по формулам (3.2) и (3.3).

Из сопротивления материалов известно, что максимальные сдвиговые напряжения в изгибаемой по трехточечной схеме балке равны:

.

Это справедливо как для изотропных, так и для изотропных материалов, но у первых прочность при сдвиге высока, и от касательных напряжений они практически никогда не разрушаются. В слоистых же материалах с низкой прочностью при межслойном сдвиге максимальные касательные напряжения при малых отношениях l/h могут превысить предел прочности при сдвиге. В результате материал разрушается из-за расслоения вблизи нейтральной оси образца - балки, в отличие от разрушения под действием нормальных напряжений, сопровождаемого первоначальным разрывом поверхностных растянутых или сжатых слоев.

На практике существует не одно значение, а интервал значении l/h, в котором наблюдается смешанное разрушение от обоих видов напряжений. Связано это с тем, что прочность при сдвиге имеет разброс из-за несовершенства технологии.

Для испытания армированных пластиков на межслойный сдвиг в стандартах рекомендуется выбирать образцы с l/h» 5, а для испытаний на чистый изгиб с l/h > 30 ¸ 40 (см. дальше). В отношении армированных металлов рекомендаций по выбору размеров образцов нет. Размеры подбирают экспериментально.

Чтобы избежать ошибок в интерпретации полученных результатов, при испытании на изгиб всегда следует указывать вид разрушения образца. Поскольку в образцах с малым отношением l/h напряженное состояние неопределенно, результаты испытаний можно использовать только для качественного сопоставления сопротивления различных материалов межслойному сдвигу.

Дата добавления: 2014-01-05