Виды межфазного взаимодействия

В соответствии с классификацией А. Меткалфа по видам межфазного взаимодействия все КМ делятся на три класса. К первому относятся КМ, у которых волокна и матрица взаимно нерастворимы и не образуют химических соединений, ко второму – КМ, у которых волокна и матрица образуют друг с другом твердые растворы и не образуют химических соединений, к третьему – КМ, у которых волокна и матрица взаимодействуют с образованием химических соединений. Такая классификация условна, поскольку КМ, содержащие волокна и матрицу на основе одних и тех же компонентов, могут относиться к различным классам в зависимости от концентрации легирующих элементов, условий получения и эксплуатации. Например, КМ с матрицей из чистой меди, армированной вольфрамовыми волокнами, относится к первому классу; если медь легирована небольшим количеством титана, этот же КМ следует отнести ко второму классу, так как в данной системе уже появляется взаимная растворимость; при повышенных концентрациях титана на поверхности раздела появляются интерметаллические соединения и КМ следует отнести к третьему классу.

Таблица 4.1.

Классификация КМ по видам межфазного взаимодействия

Первый класс	Второй класс	Третий класс
Алюминий - нержавеющая сталь *; Ag-Al2O3; Al-B *; Al-B/BN; Al-SiC *; Cu-Al2O3; Cu-W; Mg-B	Направленные эвтектики; Nb-W; Ni-C; Ni-W (выше 1233 К)	Al-C (выше 973 К); Al-SiO2; Ti-Al2O3; Ti-B; Ti-SiC
П р и м е ч а н и е. Звездочкой обозначена система псевдопервого класса; B/BN означает бор, покрытый нитридом бора.

Существуют, например, КМ псевдопервого класса. Это – системы, состоящие из кинетически совместимых компонентов, в которых принципиально возможно образование новых химических соединений на поверхности раздела. Однако оптимальная технология позволяет избежать их появления в ходе технологического цикла, а эксплуатация осуществляется при достаточно низких температурах, исключающих возможность прохождения химической реакции. Например, КМ Al-В, полученный пропиткой борных волокон расплавленным алюминием, относится к третьему классу, так как при изготовлении композиции на границе раздела волокно - матрица образуется слой борида алюминия. Однако этот же КМ, полученный по оптимальной технологии диффузионной сварки, следует отнести к КМ псевдопервого класса (табл. 4.1), поскольку реакция образования борида не успевает пройти.

Влияние поверхности раздела на прочность и характер разрушения

Прочность поверхности раздела может быть как выше, так и ниже прочности матрицы. Часть свойств КМ определяется прочностью границы раздела на отрыв (поперечная прочность, прочность на сжатие, вязкость, разрушения), часть – прочностью границы раздела на сдвиг (продольная прочность при растяжении КМ, армированных короткими волокнами; критическая длина волокон и т. п.).

Для КМ третьего класса (см. табл. 4.1) различают три участка на графике зависимости прочности КМ от толщины реакционной зоны х₃. На первом участке выраженной зависимости σ_в от х₃, не наблюдается. Здесь толщина реакционной зоны мала (в среднем 0,5-4 мкм), концентрация напряжений в ней меньше, чем концентрация напряжений, обусловленная дефектами самого волокна. Критическое значение толщины реакционной зоны х¢_кр, соответствующее первому участку рассчитывается по формуле:

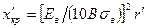, (4.5)

где:

В – коэффициент, зависящий от распределения напряжений вблизи вершины трещины;

r¢ – радиус кривизны в вершине трещины. При х₃ < х¢_кр трещины в реакционной зоне не влияют на прочность волокна.

На втором участке прочность КМ с увеличением толщины реакционной, зоны снижается. Здесь х₃ > х¢_кр и концентрация напряжения в зоне выше концентрации напряжений от собственных дефектов волокон. Средние размеры реакционной зоны для различных КМ, соответствующей второму участку, составляют 0,5-10 мкм. Существует вторая критическая толщина зоны х²_кр, которая оценивается по формуле

(4.6)

где:

Е_пр, σ_пр – модуль упругости и предел прочности продуктов реакции.

В пределах х¢_кр £ х₃ £ х^п_кр прочность КМ снижается с увеличением х₃. Предельная деформация e_f до разрушения волокон в КМ связана с х₃ зависимостью

. (4.7)

Третий участок начинается при значениях х₃ > х²_кр. Здесь прочность волокон равна прочности продуктов реакции и не зависит от толщины реакционной зоны.

Более точные уравнения зависимости критической толщины зоны взаимодействия х_кр от параметров волокна и продукта взаимодействия при отсутствии остаточных напряжений получены путем применения статистической теории прочности и линейной механики разрушения.

В первом случае это:

, (4.8)

где:

d_f – диаметр волокна;

E_f – модуль упругости волокна;

E_L – модуль упругости продукта взаимодействия;

– среднее значение прочности волокна;

– среднее значение прочности продукта взаимодействия;

b_L – вейбулловский коэффициент распределения прочности продукта взаимодействия, связанный с коэффициентом вариации прочности материала m = b^-0,92.

Во втором случае расчетное уравнение выглядит следующим образом:

, (4.9)

где:

с – половина длины трещины в слое продукта взаимодействия;

– коэффициент неоднородности.

Эти уравнения позволяют также оценить влияние толщины покрытий на армирующих волокнах на их прочность.

Экспериментальные данные о влиянии толщины покрытий различного состава на борных волокнах, полученные расчетом по уравнениям (4.8) и (4.9) приведены в таблице 4.2. Удовлетворительное согласие их с экспериментом для покрытий из карбида бора и особенно для покрытия диборида титана указывает на правильность представлений, принятых при выводе этих формул.

Таблица 4.2.

Дата добавления: 2014-01-05