Смачивание и растекание

Способность смачивать твердые тела – важная характеристика взаимодействия жидкости с поверхностью твердого тела. На практике с явлением смачивания приходится встречаться при плавке, нанесении защитных покрытий, пропитке, спекании в присутствии жидкой фазы, пайке и в ряде других процессов.

Капля жидкости на поверхности твердого тела приобретает вид, изображенный на рис. 4.9, в зависимости от природы жидкости, твердого тела и среды. Краевой угол q характеризует смачивание и может быть определен весьма точно экспериментальным путем.

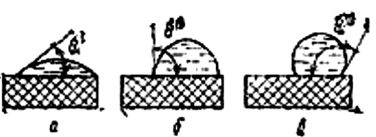
Рис. 4.9. Капля жидкости на поверхности твердого тела: а – полное смачивание;

б – смачивание; в – несмачивание

Т. Юнгом получены два уравнения, показывающие зависимость краевого угла смачивания от характеристик жидкости и твердого тела:

(4.18)

и

, (4.19)

где:

s – удельные свободные поверхностные энергии на границах раздела твердое тело - газ, твердое тело - жидкость, жидкость - газ;

W_а – работа адгезии.

Работа адгезии W_а, по определению Н.К. Адама, представляет собой работу, которую нужно затратить против адгезионных сил для отрыва твердого тела от жидкости в направлении нормали к их поверхности раздела. Дюпре показал, что работа адгезии между двумя жидкостями равна сумме поверхностного натяжения обеих фаз, взятых порознь, минус межфазное натяжение их границы раздела:

. (4.20)

Н.К. Адам указывает, что уравнение Дюпре применимо и к адгезии между твердым телом и жидкостью, причем оно может быть вычислено из значений краевых углов смачивания по формуле

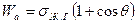. (4.21)

Существует другой метод расчета работы адгезии, предложенный Ю.В. Найдичем на основании теории скатывания капель по наклонной плоскости поверхности твердого тела, развитой Я.И. Френкелем.

Оказалось, что

,

где:

m – масса капли;

a – угол наклона;

r – радиус основания капли.

Таким образом, экспериментально по критическим углам скатывания можно определить величину W_а, по которой с помощью уравнения (4.19) возможно вычислить краевой угол. Сравнивая эту величину с краевым углом, полученным экспериментально, можно установить его справедливость. Такое сравнение полностью подтвердило принципиальную правильность фундаментальных уравнений капиллярности (4.18) и (4.19).

Следует отметить, что уравнения (4.18) и (4.19) справедливы, когда капля жидкости в контакте с поверхностью твердого тела находится в состоянии термодинамического равновесия, т. е. DF = 0, где DF – изменение свободной поверхностной энергии системы.

Несложный анализ уравнения(4/18) показывает, что смачиваемость при q < 90° улучшается с увеличением s_Т.Г, снижением s_Ж.Г и s_Т.Ж; при q > 90° снижение s_Ж.Г приводит к ухудшению смачивания, т. е. к увеличению q. Ясно также, что краевой угол не может быть равен нулю, если s_Ж.Г > s_Т.Г при s_Ж.Г > 0.

Существует большое количество способов определения смачивания, которые могут быть подразделены на методы:

1) позволяющие непосредственно измерять наклон поверхности жидкости к поверхности твердого тела;

2) определяющие какой-либо параметр контактной системы, зависящей от краевого угла смачивания.

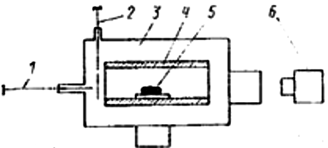
Рис. 4.10. Схема установки для определения поверхностного натяжения и краевых углов смачивания металлических жидкостей: 1 – горизонтальный шток; 2 – вертикальный шток; 3 – вакуумная камера; 4 – печь; 5 – образец металла; 6 – фотокамера

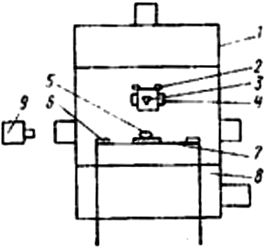
Рис. 4.11. Схема установки для изучения смачивания с раздельным нагревом: 1 – крышка; 2 – ввод тока к верхнему нагревателю; 3 – капельница; 4 – нагреватель; 5 – капля; 6 – ввод тока к нижнему нагревателю; 7 – пластина-нагреватель; 8 – камера установки; 9 – кинокамера

Для измерения краевых углов смачивания твердых тел металлическими расплавами чаще всего применяют метод лежащей капли, уже рассмотренный выше, для реализации которого пользуются специальной измерительной аппаратурой (рис. 4.10).

Недостатком указанной установки является невозможность сформировать каплю на поверхности твердого тела без их предварительного контакта в твердом состоянии. В МИСиС предложена установка, позволяющая нагревать раздельно твердую фазу и исследуемый металл до необходимой температуры, после чего жидкую каплю наносят на твердую поверхность (рис. 4.11). Это важно, если между твердой подложкой и жидким металлом происходит интенсивное взаимодействие.

Растекание или полное смачивание представляет особый интерес. В этом случае краевой угол близок или равен нулю. Растекание встречается, в частности, при смачивании жидкими титаном, цирконием, гафнием, кремнием графита. Использовать краевой угол в качестве критерия смачивания в этих системах уже нельзя. Поэтому возникает необходимость в изыскании нового критерия, характеризующего взаимодействие в таких системах. Таким критерием может явиться скорость растекания, конечный радиус капли жидкости, которая полностью смачивает твердое тело, или отношение площади, занятой растекшейся каплей, к ее массе («удельная растекаемость»).

Для изучения процесса растекания используется динамический метод, так как обычно явление растекания встречается в системах, где взаимодействие между компонентами достаточно энергичное. На рис. 4.12 показана схема установки, которая применяется для этой цели. Установка состоит из герметичного корпуса, внутри которого размещены два нагревательных элемента сопротивления. Одни из них (нижний) расположен горизонтально и служит для нагрева подложки, второй (верхний) расположен вертикально и служит для расплавления металла и образования капли. Металлический образец помещается в нем на коническом каплеобразователе, с нижнего среза которого капля падает на поверхность подложки. Расстояние между ними зависит от размера капли, но не должно превышать 10 мм. Процесс растекания фиксируется сверху на кинопленку для определения скорости растекания. Радиус растекшейся капли и ее площадь можно измерять после охлаждения образца.

По Харкинсу, процесс растекания характеризуется коэффициентом растекания, который применительно к жидкости и твердому телу имеет вид

. (4.22)

Рис. 4.12. Схема установки для исследования процесса растекания: а – схема установки; б – приспособление для плавки металла; 1 – кинокамера; 2 – смотровое окно; 3 – вертикальный нагреватель для металла; 4 – устройство для плавки металла; 5 – горизонтальный

нагреватель для подложки; 6 – горизонтальная площадка для установки образца; 7 –

вакуумное соединение; 8 – устройство, обеспечивающее горизонтальное положение

образца; 9 – груз; 10 – водоохлаждаемые токозводы; 11 – трубка; 12 – конический каплеобразователь

Этот коэффициент представляет собой выигрыш свободной энергии системы, возникающий в результате процесса растекания. Чем он более положителен, тем более полно должен протекать процесс растекания. Из уравнения (4.22) видно, что коэффициент растекания возрастет при увеличении поверхностной энергии твердой поверхности, является стремление системы к уменьшению свободной энергии за счет увеличения площади контакта жидкости и твердого тела, т. е. DF < 0. Изменение свободной поверхностной энергии системы капля - подложка можно записать следующим образом:

.

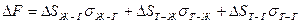Приняв, что DS_Ж-Г = DS_Т-Ж = DS_Т-Г (это справедливо для случая полного растекания), получим формулу для определения движущей силы растекания:

, (4.23)

где:

Ds – изменение удельной свободной поверхностной энергии системы.

Считается, что чем более отрицательна величина Ds, тем энергичнее должно происходить растекание. Это выражение с точностью до знака совпадает с коэффициентом растекания Харкинса.

Однако значение Ds в процессе растекания от сферической капли (q = 180°) до полного растекания (q» 0°) существенно изменяется. Чтобы оценить это изменение во времени, необходимо учесть форму растекающейся капли.

Рис. 4.13. Схема растекания капли жидкости

Предположим, что капля жидкости (рис. 4.13) растекается таким образом, что за единицу времени фронт растекания передвинулся на величину Dh.

При этом происходит уменьшение поверхности раздела твердое тело - газ и прирост поверхности раздела жидкость - газ. Вследствие этого совершается работа

.

Движущая сила растекания, пропорциональная изменению свободной поверхностной энергии системы, равна

или

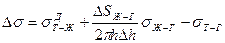
Дальнейшее решение сводится к геометрической задаче об изменении поверхности капли DS_Ж-Г при растекании. Поверхность капли, которая представляет собой шаровой сегмент, равна

.

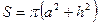При растекании происходит изменение всех переменных; следовательно, изменение поверхности можно выразить как

.

После взятия частных производных

или, заменяя дифференциалы на приращения, можно получить

.

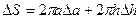На рис. 4.13 видно, что малая хорда является биссектрисой угла q. Следовательно:

и

.

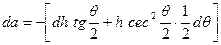На конечной стадии растекания динамический краевой угол практически не изменяется (dq» 0).

.

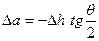Окончательно

.

Таким образом

. (4.24)

Легко видеть, что в этом выражении влияние величин 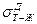(индекс «д» означает, что имеется в виду динамическая межфазная энергия и изменяющийся в процессе растекания краевой угол) и s_Т-Г на движущую силу растекания аналогично их влиянию в коэффициенте растекания Харкинса и в выражении (4.23).

В процессах смачивания и растекания определяющую роль играет уменьшение межфазной энергии на границе твердое тело - жидкость. Одним из процессов, приводящих к снижению межфазной поверхностной энергии, является адсорбция атомов или ионов на поверхности раздела жидкость - твердое тело.

Гиббс вывел уравнение, связывающее адсорбцию с поверхностной энергией

,

где:

Г – избыточная поверхностная концентрация компонента системы, понижающего межфазную энергию;

s – межфазная поверхностная энергия;

а – активность межфазно активного компонента в жидкой фазе.

Если коэффициент активности можно принять за постоянную величину, то активность пропорциональна концентрации С и уравнение Гиббса принимает вид

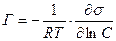
или после интегрирования

,

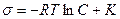где К – постоянная интегрирования.

Из этого уравнения видно, что межфазная поверхностная энергия линейно уменьшается с увеличением адсорбции межфазно активного компонента на межфазной границе.

Считают, что этот процесс приводит к понижению величины s_Т-Ж в системах Fe-Al₂O₃ и Ni-Al₂O₃ при добавке титана, хрома и кремния к железу или никелю.

Другой, не менее интересный случай понижения межфазной энергии осуществляется при наличии диффузии через межфазную границу. Например, когда жидкость находится в контакте с твердым телом, имеющим значительную растворимость в нем, на межфазной границе устанавливается диффузионный градиент. Межфазная энергия при этом изменяется по мере изменения состава жидкости. В работах Гуменика показано, что межфазная энергия в системах графит - жидкий, переходный металл при наличии диффузионного градиента на границе раздела может уменьшиться на 1000-2000 эрг/см².

А.А. Жуховицкий и В.А. Григорян на основе термодинамики необратимых процессов показали, что любой переход компонента через межфазную границу приводит к уменьшению межфазной поверхностной энергии. Поскольку наиболее общим условием возможности перехода является существование градиента химического потенциала i -того компонента в первой и второй фазах, установлено, что градиент химического потенциала Dm непосредственно приводит к изменению межфазной поверхностной энергии

,

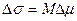где:

М – число поверхностного переноса, равное количеству перешедшего вещества через 1 см² площади в отсутствие градиента химического потенциала.

Практический интерес представляет количественное рассмотрение влияния химической реакции на межфазную энергию на границе твердое тело - газ на основе равновесной термодинамики.

Общее условие растекания жидкости по поверхности вердого тела запишем в этом случае следующим образом:

,

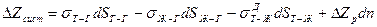где:

DZ_р – парциальное изменение изобарно-изотермического потенциала химической реакции (р, T = const);

dn – количество прореагировавшего вещества в долях моля.

Когда краевой угол растекания близок к нулю, можно считать, что

.

В условиях, близких к равновесным, можно, очевидно, записать уравнение

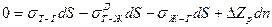
или

Интегрируя, получим

,

где:

S – площадь 1 моля вещества, растянутого в мономолекулярную пленку.

Окончательно

. (4.26)

Из этого уравнения следует, что по мере возрастания интенсивности химического взаимодействия увеличивается отрицательное значение DZ_p и динамическая межфазная энергия, уменьшается. В равновесных условиях DZ_р = 0 и уравнение (4.26) превращается в уравнение Неймана при cosq = 1.

В заключение следует отметить, что изменение межфазной поверхностной энергии на границе твердое тело - жидкость наиболее сильно влияет на смачиваемость в высокотемпературных системах, где обычно осуществляется интенсивное химическое взаимодействие.

Количественной характеристикой процесса растекания является его скорость или зависимость типа: r = f(t), где r – радиус растекающейся капли, t – врем растекания.

Существует много теорий растекания, рассмотрение которых выходит за рамки настоящего курса лекций.

Один из подходов к решению этого класса задач заключается в следующем.

Пусть убыль свободной энергии системы при растекании Ds (см. выше). «Тянущая сила» растекания равна

,

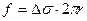где:

r – радиус растекающейся капли в момент времени t.

Сила вязкого сопротивления в соответствие с законом Ньютона определяется как:

,

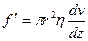где:

– градиент скорости жидкости по высоте слоя z;

h – коэффициент динамической вязкости жидкости.

При установившемся движении жидкости сумма сил, действующих на каплю равна нулю, т.е. f + f¢ = 0 или

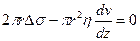(4.27)

После интегрирования этого уравнения получается выражение:

, (4.28)

где:

m – масса растекающейся капли;

r – плотность жидкости;

c – коэффициент.

Далее необходимо учесть влияние силы тяжести на процесс растекания:

, (4.29)

где

k – коэффициент, учитывающий вклад силы тяжести в процесс растекания (k = 0,5 ¸ 0,7).

В результате интегрирования этого уравнения получается следующая зависимость:

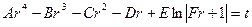, (4.30)

где:

,

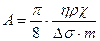остальные члены описывают влияние силы тяжести на растекание капли жидкости по горизонтальной поверхности твердого тела.

Для дальнейшего приближения расчетов к реальным условиям растекания необходимо учесть возможное изменение физико-химических характеристик жидкости и всей системы жидкость - твердое тело. При этом следует ожидать, прежде всего, изменения движущей силы процесса растекания. Учет этого изменения можно сделать с помощью уравнений (4.24) и (4.26). Далее при интегрировании дифференциального уравнения (4.29) учесть изменения вязкости жидкого в процессе взаимодействия с поверхностью твердого тела, которые определяют экспериментально.

Во всех уравнениях рассмотренной выше теории смачивания и растекания присутствуют величины свободной поверхностной энергии жидкости твердого тела и свободной поверхностной энергии на межфазной границе жидкость - твердое тело.

Методы теоретического расчета этих величин и экспериментальные методики их измерения рассмотрены ниже.

Дата добавления: 2014-01-05