Кристаллическое строение металлов

Закономерное расположение атомов в кристалле опи­сывается кристаллической решеткой, т.е. трехмерным, периодически повторяющимся расположением атомов во всем объеме кристалла. Наи­меньший объем, который характеризует особенности строения кристалла данного металла, называется элементарной ячейкой. Последовательные пере­мещения элементарной ячейки на определенные расстояния, называе­мые трансляциями решетки, позволяют последовательно пройти все области кристалла. Ячейки, или кристаллические решетки характеризуются следующими основными параметрами: симметрией, пе­риодами решетки, координационными числами и коэф­фициентами компактности решетки.

Большинство металлов кристаллизуется в трех типах решеток: гранецентрированной кубической, объемно-центрированной кубической и гексагональной, которая может быть плотноупакованной и неплотноупакованной. Эти три типа решеток приведены на рис. 2.

Периодом кристаллической решетки называется расстояние между центрами двух соседних атомов, расположенных вдоль рационально выбранных осей ячейки (при таком выборе обеспечивается ее минимальный объем). Периоды решетки измеряют в нанометрах – нм (10^{-9 м), либо в ангстремах - А (1 нм = 10 А, 1 А = 10-10 м).}

У большинства металлов периоды решеток находятся в пределах от 0,25 до 0,55 нм.

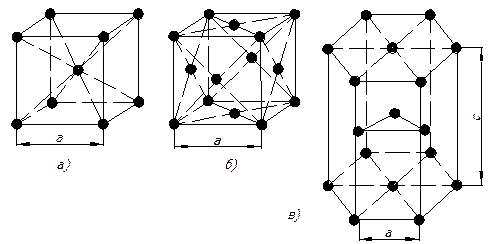
Рис. 2. Элементарные ячейки плотноупакованных кристаллических решеток:

а - объемно-центрированная кубическая; б - гранецентрированная кубическая;

в - гексагональная плотноупакованная; а и с – параметры решеток

Координационным числом (К) называется количество атомов, находящихся на наиболее близком и одинаковом расстоянии от любого произвольно выбранного атома в решетке. Координационное число для объемно-центрированной кубической (ОЦК) решетки равно 8 (атом в центре куба имеет 8 соседей). Для гранецентрированной кубической решетки (ГЦК) координационное число - 12. В гексагональной плотноупакованной решетке (ГПУ) координационное число также равно 12.

Базисом решетки называют количество атомов, при­ходящихся на одну элементарную ячейку. При этом, как уже отмечалось, надо иметь в виду, что атомы в углах ячеек принадлежат одновременно 8 ячейкам, атомы, расположенные в центрах граней - двум ячейкам. Тогда, базис ГЦК решеток равен 4, базис ОЦК составляет 2 и базис ГПУ равен 6.

Коэффициент компактности решеткиh определяется отношением объема, занимаемого атомами с условно сферической формой V_a, ко всему объему ячейки V_p, т.е.

h = V_a/V_p. (1)

Для ОЦК решеток коэффициент ком­пактности равен 0,68, для ГЦК и для ГПУ решеток он равен 0,74 (при с/а = 1,633).

При решении задач, стоящих перед металлографией, необходимо иметь систему обозначений для записи ориентации граней кристалла и плоскостей, расположен­ных внутри кристалла.

Эти обозначения должны давать лишь ориентацию, но не обязательно определять кон­кретное положение плоскостей в кристалле. Для этой цели приняты индексы Миллера(h, k, l). В отличие от естественной записи положения плоскости величинами отрезков, отсекаемых ею на осях координат (на трех ребрах элементарной ячейки), эти индексы записывают в обратных величинах, т. е. индексы Миллера соответст­вуют величинам обратным величинам отрезков, отсекае­мых плоскостями на осях координат. Величины же от­резков выражаются числом периодов трансляции. Если плоскость направлена параллельно одной из осей коор­динат, то считается, что она пересекает эту ось в беско­нечности и индекс будет равен нулю, если параллельно двум осям - то два индекса равны нулю (рис. 3).

Что­бы определить индексы Миллера необходимо выпол­нить следующие действия: найти отрезки, отсекаемые плоскостью на осях координат, измеренные в осевых единицах (периодах решетки), взять обратные значения этих чисел и привести эти значения к целым числам. На­пример, рассматриваемая плоскость (рис. 3, б) отсекает на оси Х отрезок равный 1, на оси Y — равный 2/3, на оси Z —1/2 периодов трансляций. Тогда отрезки, обратные указан­ным, будут равны 1, 3/2 и 2. После приведения этих дро­бей к общему знаменателю получим числители равные индексам данной плоскости, т.е. h = 2, k = 3, l = 4. Полу­ченные числа записывают в указанном порядке и заклю­чают в круглые скобки: (234).

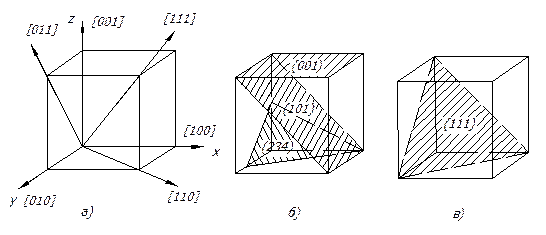
Рис. 3. Кристаллографические индексы направлений (а)

и плоскостей (б, в) в кубических решетках

При индицировании направлений, одну точку прямой помещают в начало координат, а другую получают пу­тем последовательного векторного сложения 3-х переме­щений, параллельных трем осям координат. Например, точка на прямой, проходящей через начало координат, смещается на Н осевых единиц вдоль оси X, К осевых единиц вдоль оси Y и L единиц вдоль оси Z.

Тогда, если Н, К, и L - три взаимно простых числа, то они являются индексами направления.

При этом важно отметить, чти при определении индексов направлений не нужно поль­зоваться обратными значениями длин отрезков, отсе­каемых на осях координат. В отличие от индексов плос­костей, индексы направлений принято заключать в квад­ратные скобки, например, [121] или [130]. Индексы наиболее часто встречающихся плоско­стей и направлений для кубических решеток приведены на рис. 3.

Одним из наиболее распространенных и прямых мето­дов определения типа кристаллических решеток и разме­ров элементарных ячеек является метод рентгеноструктурного анализа. Возможно также определение этих величин с помощью дифракции электронов и нейтронов.

Дата добавления: 2014-01-05