Displacement and velocity

PARTICE KINMATICS

Many objects that physicists study, from atoms to galaxies, are in motion. Motion may be orderly or random, steady or intermittent, or even a confusing mixture of these. We cannot hope to gain insight into how nature works unless we can clearly define and then measure motion. The subject of kinematics is concerned with the description of how a body moves in space and time. In translational motion, all parts of a body undergo the same change in position. In rotational motion the body changes its orientation in space. In vibrational motion the shape or size of the body changes rhythmi­cally. This chapter is restricted to translational motion along a line; that is, one-dimensional kinematics.

The translational motion of an object can be completely described by the movement of any single point on it. Consequently, the object may be treated as a particle. In everyday language, the word "particle" implies something tiny, al­most invisible. In physics, however, a particle is an idealized model of a real object that allows us to locate it at a single point in space. The particle model is a useful simplification when the size, shape, and internal structure of the system under study are of no interest. For example, when we study the orbital motion of the earth about the sun, the earth may be considered to be a particle. However, if we wish to study earthquakes, tides, or hurricanes, the earth's internal structure and rotational motion become significant and it would not be adequate to treat the earth as a particle.

Suppose we wish to study the translational motion of a car along a straight road. We may treat the car as a particle and use the road as a frame of reference. For one-dimensional motion, we need just one axis to locate the particle. We take our x axis to lie along the road (see Fig. 2.1). In Chapter 1 we defined displacement as a change in position and noted that it is a vector. When a particle moves from an initial coordinate x _i to a final coordinate x _f, its displacement is written as

FEGURE 2.1

∆ x = x _f − x _i (2.1)

Displacement is a vector quantity which refers to "how far out of place an object is"; it is the object's change in position.

The Greek letter ∆ (capital delta) is usually used to signify the change in the variable that follows it. Note that ∆ x always means the final value minus the initial value, not the greater minus the lesser. The sign of ∆ x indicates its direction relative to the + x axis. In Fig. 2.1 the particle starts at point A (x _i = 2 m) and stops at point В (x _f = 6 m), having turned around at x = 9 m. Its displacement, ∆ х = 6 − 2 = +4 m, depends only on the initial and final positions, not on the details of the journey.

The distance traveled − that is, the length of the actual path — is a positive scalar which refers to "how much ground an object has covered" during its motion.

Its value for the journey in Fig. 2.1 is 10 m. In general, the distance traveled between two points is not equal to the magnitude of the displacement between the same two points.

A basic question regarding the motion of a particle is how fast it moves. The average speed for a finite time interval is defined as

Average speed = Distance traveled / Time interval (2.2)

Since it is defined in terms of distance, average speed is also a positive scalar. (We will not use a symbol for average speed.) In contrast, the average velocity for a finite time interval is defined as

Average velocity = Displacement / Time interval

Average velocity is a vector in the direction of the displacement. The average velocity depends only on the net displacement and the time interval; the details of the journey in between are of no consequence. Since we are concerned only with motion along the x axis, the x component of the average velocity is

(2.3)

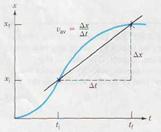
FIGURE 2.2	FIGURE 2.3

where ∆ t = t _f – t _i. The SI unit of both speed and velocity is m/s. The sign of υ _av is the same as that of the displacement. Positive υ_av means that the net motion is in the direction of the + x axis. For the motion depicted in Fig. 2.1, suppose it took 4 s to go from A to B. The average speed would be (10 m)/(4 s) = 2.5 m/s, whereas the average velocity would be υ_av = (+4 m)/(4 s) = +1 m/s.

The motion of a particle is often presented in graphical form. The features of the graph allow us to quickly extract information on the history of the particle's motion. If the position of a particle moving at constant velocity were recorded on a paper tape, at 1 s intervals, say, the dots would be equally spaced as in Fig. 2.2 a. The corresponding x versus t graph (Fig.2.2 b) is a straight line. Since υ _av = ∆x/∆t, we see that the average velocity is given by the slope of the x versus t graph. When the motion is not at constant velocity, the graph of x versus t might look like Fig. 2.3. In general, the x component of the average velocity for any time interval ∆ t is given by the slope of the line joining the initial and final points on the x versus t graph.

Дата добавления: 2014-01-05