Работа при поступательном и вращательном движении

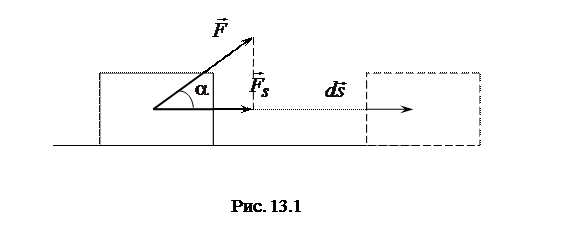
Пусть тело под действием силы F перемещается за некоторый промежуток времени на расстояние ds (рис. 13.1). При этом вектор 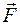с направлением перемещения 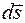составляет угол 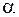. Работой в механике называют величину, равную произведению модуля вектора силы на модуль вектора перемещения и на косинус угла между этими векторами.

Для элементарной работы имеем

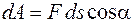. (13.1)

Из рисунка 13.1 следует, что

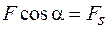, (13.2)

где – проекция вектора силы на направление перемещения. Объединяя выражения (13.1) и (13.2), получаем

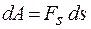. (13.3)

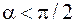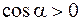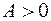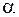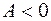Работа – скалярная величина. Если направление вектора силы с направлением перемещения образует острый угол (), то и . Если угол – тупой (), то и . При 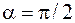работа .

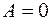Единица работы - джоуль (Дж). За один джоуль принимается работа, совершенная силой в один ньютон при перемещении тела на один метр в направлении действия силы.

Если при перемещении значение силы и ее направление на отрезке пути не изменяются, работа определяется выражением

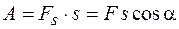. (13.4)

Работа переменной силы на некотором пути может быть вычислена как сумма бесконечно большого числа элементарных работ:

. (13.5)

В этой формуле должна быть известна зависимость силы от положения тела в пространстве на всем участке траектории движения от положения 1 до положения 2.

На практике важно не только значение совершенной работы, но и время, в течение которого она совершается. Работа, совершенная за единицу времени, называется мощностью. Если работа dА совершена за время dt, то мощность равна

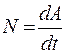. (13.6)

Если мощность не меняется с течением времени, то она определяется выражением

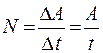. (13.7)

Единица работы – ватт (Вт). Из формулы (13.6) или (13.7) следует, что один ватт – это мощность, при которой за каждую секунду совершается работа, равная одному джоулю.

Подставляя выражение (13.4) в уравнение (13.6), получим

;

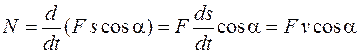. (13.8)

Мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между ними.

Найдем работу, которую совершают внешние силы при повороте тела вокруг неподвижной оси (рис. 13.2).

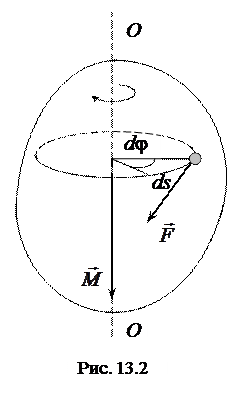Пусть к некоторой точке тела приложена сила вызывающая вращение точки по окружности радиусом r. За некоторое время dt радиус-вектор точки повернется на угол d j, а точка переместится по дуге окружности на расстояние

.

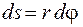При движении материальной точки силой F совершена работа

.

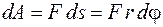Так как 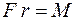– момент силы относительно оси вращения, то для работы получаем выражение

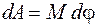. (13.9)

Эта формула применима для твердого тела при условии, что М - момент всех сил, действующих на тело. Полная работа при вращении тела

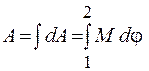. (13.10)

Дата добавления: 2014-01-05