Потенциальная энергия

Потенциальная энергия обусловлена взаимодействием тел или частей одного и того же тела. Значение потенциальной энергии зависит от характера сил взаимодействия тел или от характера силового поля, в котором находится тело.

Рассмотрим потенциальную энергию упруго деформированного тела (сжатой или растянутой пружины). Энергия в данном случае определится взаимным расположением частей одного и того же тела (витков пружины). Пусть начальное состояние соответствует положению равновесия пружины. Сила упругости пропорциональна деформации:

,

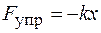где k - коэффициент упругости, х - значение деформации.

По третьему закону Ньютона деформирующая сила равна по модулю силе упругости и противоположна ей по направлению, т. е.

.

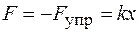При малых значениях деформации dх совершается элементарная работа

. (15.1)

Если значение деформации меняется от 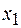до , то при этом будет совершена работа

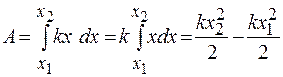. (15.2)

Так как работа равна изменению потенциальной энергии пружины, то

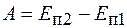. (15.3)

Сравнивая выражения (15.2) и (15.3), для энергии упруго деформированного тела имеем

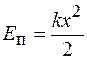. (15.4)

Найдем теперь потенциальную энергию тела в однородном поле силы тяжести, т. е. энергию тела, поднятого на некоторую высоту над землей (рис. 15.1).

Пусть тело массой m перемещается с высоты 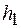над поверх-ностью земли до высоты 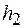по некоторой произвольной траектории. Выберем элементарный участок траектории ds, направление которого составляет с направлением силы тяжести угол 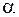. Работа силы тяжести на этом участке равна

.

Из рисунка 15.1 находим, что .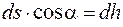

Тогда получаем элементарную работу в виде

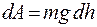. (15.5)

Полная работа на всей траектории будет определяться выражением

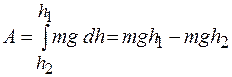. (15.6)

Так как эта работа связана с изменением положения тела относительно земли, то она определяется изменением потенциальной энергии тела, т. е.

.

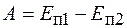Тогда для энергии тела массой m, поднятого над землей на высоту h, получаем

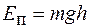. (15.7)

Из формулы (15.6) следует, что работа силы тяжести не зависит от формы траектории, по которой перемещается тело, а определяется только начальным (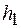) и конечным (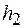) положением тела. В любой системе, в которой выполняется это условие, работа совершается за счет изменения потенциальной энергии, т. е.

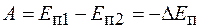, (15.8)

где 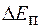- приращение энергии.

Силы, работа которых не зависит от формы траектории, называются консервативными, системы, в которых они действуют, - консервативными системами.

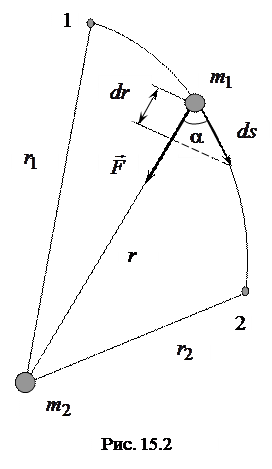Рассмотрим теперь потенциаль-ную энергию тела в поле центральных сил. Силы называются центральными, если их направление в любой точке пространства проходит через некоторый центр, а значение силы зависит только от расстояния до этого центра. Примером такой силы может служить сила гравитационного взаимодействия двух тел, определяемая законом всемирного тяготения. Анализируем движение тела массой относительно тела массой 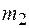по некоторой произвольной траектории (рис. 15.2).

При некотором расстоянии r между телами сила взаимодействия между ними определится выражением

.

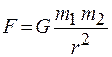Тогда для элементарной работы на отрезке траектории ds находим

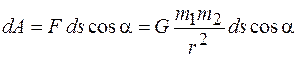. (15.9)

Из рисунка 15.2 следует, что 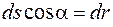. Поэтому

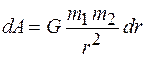. (15.10)

Если тело перемещается из положения 1, характеризуемого расстоянием между телами 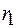, в положение 2 с расстоянием 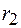, то полная работа при таком перемещении будет определяться интегралом выражения (15.10):

.

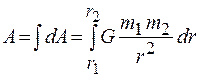Вычисление этого интеграла приводит к формуле

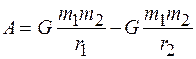. (15.11)

Эта работа определяется изменением потенциальной энергии взаимодействия тел, т. е. . Тогда из выражения (15.11) для потенциальной энергии взаимодействующих тел с массами и 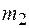, находящихся на расстоянии r друг от друга, получаем

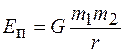. (15.12)

Во всех рассмотренных случаях при определении потенциальной энергии просматривается одна и та же закономерность: необходимо знать, относительно чего рассчитывается эта энергия. Поэтому потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это обстоятельство, однако, не имеет никакого значения, так как во все физические соотношения входит только разность значений потенциальной энергии в двух положениях тела. Практически принимают потенциальную энергию тела в каком-то определенном положении равной нулю, а энергию тела в других положениях отсчитывают по отношению к этой энергии.

Дата добавления: 2014-01-05