Теорема Гаусса

Так как поток вектора напряженности связан с напряженностью электрического поля, которая, в свою очередь, зависит от зарядов, создающих поле, следовательно, поток вектора напряженности должен быть связан с зарядами. Эта связь устанавливается в теореме Гаусса.

Рассмотрим поле точечного заряда q и вычислим поток вектора напряженности через некоторую площадку dS, расположенную в этом поле на рас-стоянии r от заряда (рис. 26.1). Для удобства полагаем, что поле создается в вакууме ().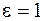

Ориентация площадки в пространстве определяется направлением вектора нормали к площадке. Вектор напряженности составляет с нормалью угол a. Поэтому поток через площадку dS определяется выражением

, (26.1)

где – проекция площадки dS на плоскость, перпендикулярную к радиусу r.

Так как поле создано точечным зарядом q, то в пределах площадки dS напряженность Е определится равенством (22.6).

Объединяя выражения (22.6) и (26.1), получаем при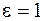

. (26.2)

В этом уравнении величина есть телесный угол d W, под которым из точки нахождения заряда q видна площадка 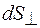, а следовательно, и площадка dS. Тогда выражение (26.2) принимает вид

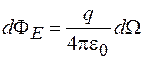. (26.3)

Поток 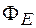через произвольную поверхность S найдем интегрированием выражения (26.3) по значению телесного угла, т. е.

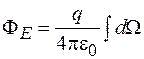. (26.4)

Если поверхность S замкнутая, то для нее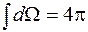. В этом случае выражение (26.4) преобразуется к виду

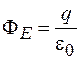. (26.5)

Заменив поток выражением через интеграл (25.1), получим

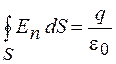. (26.6)

В соответствии с формулой (26.6) поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен отношению заряда, находящегося внутри поверхности, к электрической постоянной.

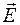Если поле создается системой точечных зарядов, то в каждой точке поля напряженность , а проекция вектора на направление нормали к площадке dS равна 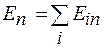. Подставим это выражение в формулу (26.6) и выполним преобразования:

.

Выражение под знаком суммы представляет собой поток вектора напряженности поля точечного заряда 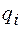, который согласно формуле (26.6) равен 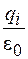. Соответственно получим

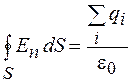. (26.7)

Формула (26.7) - математическое выражение теоремы Гаусса, согласно которой поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов внутри поверхности к электрической постоянной.

Если замкнутая поверхность не охватывает заряды (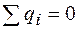), то на основании формулы (26.7) поток через такую поверхность равен .

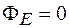При доказательстве теоремы Гаусса предполагалось, что все заряды, создающие поле, являются точечными. Однако теорему Гаусса можно использовать для поля, созданного любыми заряженными телами, так как всякий заряд можно мысленно разделить на малые части, каждую из которых можно рассматривать как точечный заряд.

Дата добавления: 2014-01-05